Teoria da Probabilidade III - aplicacoes e distribuicoes

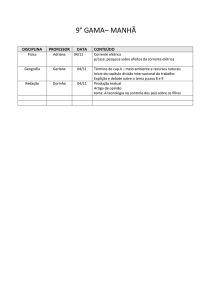
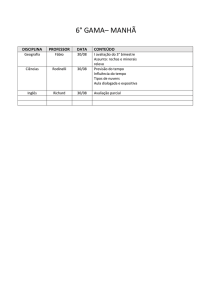
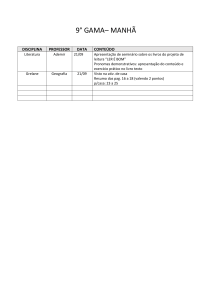
Aplicações:
Incluir as distribuições discretas: distribuição degenerada + distribuição uniforme +
distribuição multinomial
Incluir as distribuições contínuas: uniforme + exponenciais + triangulares
Distribuição de Bernoulli:
Jogar a moeda, só temos duas possibilidades, cara ou coroa. A v.a. será definida como cara = 1 e
coroa = 0. Qualquer jogo com apenas duas respostas, sim = 1 e não = 0, segue uma distribuição de
Bernoulli. Se a probabilidade de SIM é p , a de Não será q  1  p e a função densidade de
é dada por: f  x   q  x   p   x  1 . A função distribuição de probabilidade
probabilidade
acumulada vale:


F  x  


0 x0
q 0  x 1
1 x 1
A funçao geradora dos momentos é dada por: M  t  

 q  x   p  x  1 e
xt
dx  q  pet . A

função característica   t   q  pe .
it

Momentos:
Mk 
 q  x   p  x  1 x dx  q0
k
k
 p1k logo M k  p k , então   p .

1 p t
 qe  pt  pe qt .
Momentos centrados: e  t M  t   e  pt  q  pet   qe  pt  pe
Agora mk 
dk
k
 qe pt  peqt   q   p  e pt  pq k e qt
k 
dt
mk  pq 1  p 

k 1
k 1
  p  .

Casos particulares:
1.
m1  pq  qp  0 ;
k
k
, ou seja, mk  pq   1 qp ou ainda
k
t 0
2.
m2  pq 1  p   p   pq ;
3.
m3  pq 1  p   p 2   pq 1  2 p  p 2  p 2   pq 1  2 p  ;


4.
m4  pq 1  p   p3   pq 1  3 p  3 p 2  p3  p3   pq 1  3 p 1  p   pq 1  3 pq  .


2
3
Cumulantes:
ln   t   ln 1  p  eit  1 ,
então
d
ipeit
ip
ip
ln   t  
 it

 it
it
dt
p  1  p  eit
1  p  e  1 e  p  pe
logo:
1.
2.
3.
1
d
d
ln   t   ip  p  qe  it  . Logo c1  i ln   t   p
dt
dt
t 0
2
d2
2 d
2
 it
 it 2 
2

ln

t

i
pq
e
p

qe


c


i
,
logo

  2 ln   t   pq .

 
2

dt 2
dt
3
2
3
d3
ln   t   i 3 pq  2qe2it  p  qeit   eit  p  qeit    i 3 pqeit  p  qeit  p  qe it 
3


dt
logo, m3  c3   i 
3
4.
d3
ln   t   pq  q  p  .
dt 3
t 0
4
d4
ln   t   i 4 pqeit  p  2qeit  p  qeit   3qeit  qeit  p   p  qe it  .
4
dt
alguma álgebra temos
c4   i 
4
4
d4
ln   t   i 4 pqeit  p 2  4 pqeit  q 2e2it   p  qeit  , logo
4
dt
d4
ln   t   pq  p 2  4 pq  q 2  ou c4  pq 1  6 pq  .
dt 4
t 0
Distribuição Binomial:
Após
Vamos jogar a moeda n vezes de forma independente. Nesse caso a v.a. soma são i.i.d., e a função
n
característica vale:  Bin  t    Bern
 t   q  peit  . Sabendo a  queremos a f  z  dada por
n
1
f  z   FT   t   
2
1



n
q  peit  eitz dt . Expandindo em binômio de Newton temos:
n
 1
n
f  z      q nk p k 
k 0  k 
 2
 n  n  n k k
i  k  z t
e
dt
    q p   z  k 

 k 0  k 

Aqui vale a acumulação dos cumulantes ck Bin  n ck Bern , então   np ,  2  npq , c3  npq  q  p  e
c4  npq 1  6 pq .
Distribuição de Poisson:
Essa distribuição é um caso limite da binomial quando n   , mas p  0 de tal forma que o produto
   eit  1 
it
 . Nesse ponto usamos o fato de
np   é constante. Agora  Bin  t   1  p  pe   1 
n


n
n
n
que
 x
Lim 1    e x
n 
 n
f  z 
1
2

e

para
eitz dt  e
 eit 1
  
2

achar
 Poisson  t   e

 e  itz

 e e dt   e
it
k 0



 eit 1
k  1

k !  2
.
e   k
 z k .
k!
k 0

Uma expressão para FPoisson  z  .
FPoisson  z  


e   k
f Poisson  x  dx  
k!
k 0
Então FPoisson  z   e


int  z 

k 0
k
.
k!
z
   x  k  dx  e


queremos
a
    k
ikt itz
e
e
dt
 z  k
  e

k!

 k 0

f Poisson  z   
z
Agora
int  z 
k
k 0
k!

fdp:
Cumulantes: ln Poisson  t   ln e

k k
    eit  1    i t , portanto todos os cumulantes valem




 eit 1


k 1
k!
 , daí    ,  2   , m3   e m4    3 2 , a skewness vale  3 
a curtose k 
1

, sempre leptocúrtica. Se
1

 0 , skewed to the right, e
   então a skewness e curtose tendem a zero.
Distribuição Normal:
Vamos fazer o limite de n tendendo a infinito na distribuição binomial e usar o truque do logarítmo.
Nesse caso:

t2
n
ln Bin  t   Bern
 t   n ln q  peit   n ln q  p  ipt  p 
2


x 2 x3
já sabemos que ln 1  x   x 
 
2 3
Chamando x  ipt  p

k 1
 1


t2

n
ln
1

ipt

p



2


k 1
k
x k e vamos truncar a série na ordem 2.
t2
temos:
2
2


t2 
t2  
t2
t2
ln Bin  t   n ipt  p   ipt  p    n ipt  p  p 2 
2 
2 
2
2



Logo lim ln  Bin  t    inpt 
n 
vale:
 Normal  t   e
it 
ln  Normal  t    it 

 . Mas

npqt 2

2


t2

n
ipt

p
1

p





2


e essa é a distribuição normal, cuja função característica
 2t 2
2
.
 2t 2
2
Note
que,
nesse
caso,
só
existem
dois
cumulantes,
k
e
e
it 
 2t 2
2
e

 2t 2
2
pois
, c1   e c2   2 , todos os outros são nulos. Os momentos centrados
são dados pela função geradora:
 it



  2t 2 

k
k

 

1  2 k 2 k   1  2 k  2k ! t 2 k
2 




t 
.
k!
2k k !
2k k !
 2k  !
k 0
k 0
k 0
Percebe-se

 i 
k 0
2k
que
m2 k
não
existem
momentos

t 2k
t 2k
k
.
   1 m2 k
 2k  ! k  0
 2k  !
ímpares
Comparando
e
que
os
 2k  !  2 k .
m2 k 
extraímos
pares
2k k !
reescrever esse resultado em termos dos fatoriasi duplos z !!  z  z  2 z  4
 2k !!   2k  2k  2 2k  4
2 1   2k  2k  2 
logo  2k !   2k !! 2k 1!! , substituindo m2 k 
2k
Podemos
. Notando que
2  2  2   2  k  k 1 k  2  1  2k k ! e, além disso, que:
 2k !   2k  2k  1 2k  2  2k  3
simples m2k   2k 1!!
valem
2   2k  1 2k  3  1
 2k !! 2k  1!! 2 k
 2k !!
chegamos na expressão mais
4
4
6
6
. Então vemos que m2   2 ; m4   3!!  3 ; m6   5!!  15
e assim por diante.
1
Falta a função densidade de probabilidade: f  z  
2
quadrado
e

 2t 2
2
 i  t itz
no
e

expoente
 z   2
2
2

2
e

f  z 
e
e
z  
 t i 2 
2 
 
2
2
2

2
it itz
e

 2t 2
2
e
i t 
 2t 2
2
eitz dt . O truque aqui é completar

it  z   
e

2 
 z   t   z     z  
t 2  2i
2 
2
4
4

2
2


,
obtendo
2
 z   2
2

 2t 2

. Substituindo de volta na integral temos:

e
2
z  
  t i 2 
2 
 
2


 z   2
  t  e 2
d

2
 2
2

e

u 2
du 
 z   2
2 2
e
2


Finalmente obtemos a função densidade de probabilidade da distribuição Normal:

N  x;  ,   
e
 x   2
2 2
2 
A Normal Padrão tem esperança nula e variância unitária dada por NP  x  
1
cumulativa é definida como   x  
2
x
e

t2
2
e

x2
2
2
. A Normal padrão
dt . Note que é sempre possível escrever o resultado

de uma normal cumulativa em termos da   x  por uma mudança de variável. Se queremos a função
distribuição
de
probabilidade
x
1
FNormal  x  
2 
1
a FNormal  x  
2
e

 x   2
2
2

 x  


cumulativa
1
dx 
2
x
e

de
 x   2
2 2

uma
normal
com

e
,
ou
seja:
x
x
nos leva
d   a mudança de variável t 

 
 x 
e dt   
 . Por isso as tabelas da normal são sempre feitas para a
  

t2
2
normal padrão usando como argumento o desvio da esperança medido em desvios padrão z 
x

.
Distribuição Log-Normal.
A distribuição Log-Normal é obtida da Normal através da mudança de variável y  e x . A regra ára
mudança de variável é dada por f ( y ) 

f [ g 1 ( y )]
, com a somatória sobre todos os x’s possíveis
dy
dx
para as raízes da equação g ( x )  y , ou, x  g 1 ( y ) . Neste caso a função é biunívoca e só existe uma
dy
 e x  y . Logo:
dx
raiz dada por x  ln y , y  [0,  ) . Vamos precisar da derivada

LogN [ y;  ,  2 ] 
e
(ln y   )2
2 2
2  y
A log-Normal como uma aproximação da normal:

Vamos reescrever a log-normal como LogN 
e
 ln y ln yo 2
2 2
2  y

e
  y 
ln  yo  

2 2
2  y
2
 , yo  0 , e ver o que
acontece para y  yo   y com  y  yo .




Neste caso ln y  ln  yo   y   ln  yo 1 

aproximado por (ln y  ln yo )  ln 1 


vemos que LogN 
 y 
 y
   ln yo  ln 1 
 e o termo no expoente é
yo  
yo 

 y  y
. No denominador simplesmente fazemos y  yo e

yo  yo
 y2
2 2 yo2
N
e
 y . Se fizermos 
é uma normal da variável
teremos
log N 
y
yo
o
2  yo
duas curvas muito semelhantes no caso em que  N   . Note que se y  0 o ln y   anulando
a função. Grandes diferenças, portanto, entre a normal e a log-normal ocorrerão quando a
probabilidade de valores de x negativos na normal forem grandes. A figura xx mostra esse
comportamento:
Figura xxx. Normal com xo  yo  100 . (a)  N  10 e  log N  0,1 ; (b)  N  20 e  log N  0, 2 ;(c)
 N  40 e  log N  0, 4 .
Tanto a função geradora dos momentos quanto a função característica apresentam problemas de


convergência, mas podemos calcular os momentos da Log-Normal M n 
y
0
no
expoente:
Mn  e
e e

2
2

e e
( x   )2

nx
2 2
continuando
 n  n2
nx
 1

 2 
( x   )2
2 2
e

e

e

( x   )2  2 2 nx
2 2
( x   x  n )
2 2

2
binômio de Newton
variância
m2
9
3   2
2
e
dy
mudando a
2  y
e
nx

( x   )2
2 2
e
dx . O truque aqui é completar quadrado

e

x 2  2  x   2  2 2 nx
2 2
e
 n  n2

e
2
2

e

x 2  2(   n 2 ) x  (   n 2 ) 2 (   n 2 ) 2   2
2 2
( x   x  n 2 )2
2 2
.
Daí
 n  n2
2
2
.
que
Em particular temos M 0  1 ; M1  e

2
2
;
M 4  e 4  8 . Podemos calcular os momentos centrados usando
2
n
n
nk
mn      1  n k M k . Já sabemos que mo  1 e
k 0  k 
temos:
vemos

dx  . A integral entre colchetes vale 1 e temos todos os

momentos de ordem n dados por M n  e
M 2  e 2   2 ; M 3  e

( x   x  n 2 )2 (  2  2  n 2  n2 4 )   2

2 2
2 2
e
dy
 dx , quando y  0 x   e quando
y
variável de integração para ln y  x , y  e x ,
1
y   x   . Nesse caso: M n 
2 
n
(ln y   )2
2 2
m2  M 2  M12
logo
m1  0 . Para a
m2  e 2   2  e 2    e 2   (e  1) ,
2
2
2
2
V [ y]  e
2   2
2
(e 1) e
V [ y]  e

2
m3  M 3  3M1 M 2  2 M13
m3  e
m3  e
m3  e
9
3   2
2
3
3   2
2
3
3   2
2
 3e
1
 2e
e
e 3  3e  2  .


2
2
2
de
   2 2   2 2
2
2
(e  1) . Para o momento centrado de ordem 3 temos
2
3
3   2
2
onde
e
9
3   2
2
Fatorando
o
 3e
5
3   2
2
termo
extraímos
 2e
3
3   2
2
entre
que
e
colchetes
ainda
chegamos
a
e  1 e  2 . A Skewness será dada por:

 

2
3 
2
m3

V ( y)

3

e
3
3   2
2
3
3   2
2
e
2
e  1

  e 2  2  
3 

2
e  1 2


2
e
2

 1  e  2  .


2
Para o momento de ordem 4 m4  M 4  4 M1 M 3  6 M12 M 2  3M14 teremos:
m4  e
4  8 2
 4e

2
2
e
9
3   2
2
 6e 2   e 2  2  3e 4  2  e 4  8  4e 4  5  6e 4  3  3e 4 2
2
Que pode ser simplificado para m4  e
2
4   2 2
2
2
2
2
2
e 6  4e3  6e  3 e fatorando o termo:


2
2
2
2
e 6  4e 3  6e  3  e  1 e 5  e 4  e 3  3e 2  3e  3  e  1 e 4  2e 3  3e 2  3

 

 
 

2
2
2
2
2
2
2
2
2
2
2
2
2
obtemos, finalmente: m4  e 4   2 e  1 e 4  2e 3  3e 2  3 .
2
2

4 

m4
V ( y)

4
que leva à curtose k  e
 
2
2

2
e 4   2 e  1

 e 4 2  2e 3 2  3e 2 2  3  e 4 2  2e 3 2  3e 2 2  3

2 
2
2
 

e 4   2 e  1


2
Agora
2
2
 2e3  3e 2  6 . Como 1  2  3  6 percebe-se que k  0 sempre,


2
com a igualdade valendo apenas se   0 .
4 2
Distribuição Gama:
2
2
2

Função gama: Vamos calcular a seguinte integral:
I  z    t z e  t dt
. Fazendo por partes
0
b
b
 udv  uv   vdu com u  t
b
a
a
z
; du  z t z 1dt , dv  et dt e v   e  t , temos que:
a

I  z    t z e  t dt  t z e t
0
Mas t z e  t

0

0

 z  t z 1e t dt .
0

 0 , pelo t z em t  0 e pelo e  t em t   , então I  z   z  t z 1e t dt , o que nos leva à
0
I  z   z I  z 1 . Aplicando essa relação várias vezes temos que
relação de recorrência
I  z   z I  z 1  z  z 1 I  z  2 

I  z  temos que I  0    e  t dt  e t
 z  z 1 z  2 1 I  0 z  . Pela definição de

0
 1 , portanto I  z   z !.
0
A identidade acima foi mostrada apenas para Z inteiro positivo, mas dado que a integral existe ela pode
ser utilizada para generalizar a função fatorial para reais e até mesmo complexos, com a única condição


de que a integral convirja. Assim: z !  t z e  t dt . Essa integral não apresenta problemas para t   por
0
conta do e  t mas pode ter problemas para t  0 se z  0 . A integral converge se
x
 t dt
z
existe. Para
0
x
z  1 a integral  t z dt 
0
t z 1
existe se z  1  0 , ou seja, z  1 .
z  1 t 0

A função gama é definida por:   z    t z 1e  t dt , com Re Z  0 . A relação com a função fatorial é
0
dada por   z    z  1! e z !    z  1 . Formas equivalentes: vamos mudar a variável para t  x 2 e

dt  2 x dx
então
  z   2  x 2 
0
z 1
e  x x dx ,
2

finalmente
  z   2  x 2 z 1 e  x dx
2
0
e

z !  2 x
2 z 1
 x2
e
0


2
1
1
 x2
vemos que     2  e dx   e  x dx de onde extraímos
dx . Fazendo z 
2
2
0


1

que      e que  1 !   .
2
2
A distribuição gama é dada por:
f gama  x  xo ; ,   
 x  xo 
 1

e
x  xo

H  x  xo 
    
Vamos mostrar que a área sobre a curva vale sempre 1.



 1

 x  xo 
f gama  x  dx 



   xo   
1

e
x  xo


  
x
1
d 
t  1et dt 
1

  
      0
Casos particulares:
x  xo

1.
  1 então fexp onencial  x  xo ;    f gama  x  xo ;1,   
2.   v
2

e

e   2 então f  2  x  xo ;   f gama x  xo ;
H  x  xo 

2

,2 

 x  xo  2 e
1

x  xo
2
H  x  xo 
 2

2 2 
é a distribuição chi-quadrado [se pronuncia qui-quadrado].
FGM da distribuição gama:
 1

 x  xo 
M t  
e 


      
1
M t  
e xot
  
xt


0
e  tu u 1e u du 

e
e xot
  
x  xo


 1 1  t u
du 
u e
0
 1

x
e xot
x  x t  x  xo 
H  x  xo  d   
e o  


      
  
e xot
1
   1   t 

 1   t  u 
0

e
 1 1  t u
e
x  xo

 x  xo 
H  x  xo  d 

  
d 1   t  u 
M t  
e xot

1   t 
  
M  t   e xot 1   t 

 1  v
 v e dv 
0
e xot

1   t    
  

Logo   t   eix t 1  i t 
o

Esperança: M   t   xo e x t 1   t 
o
Se   0 então xo  

  e xot 1   t 
 1
então   M   0  xo   .
logo neste caso   t   e i t 1  i  t 

e  n  t   e  in t 1  i t 
 n
o que gera
uma distribuição gama com   x  n ; n ,   .
ln   t   ln e
Cumulantes:

ixot
  ln 1  i t   ixot   
k
k 1
 i   1  k t k ,

ln 1  x   
k 1
 1
k
k 1
pela série do logarítmo
k
k 1
k k
 k
x k , ou seja, ln   t   ixot    i k ! t , finalmente:
k 1

k
k!
ln   t   i  xo    t   i k  k  1! k 
k 2
tk
k!

tk
Comparando com ln   t    i ck
, da definição dos cumulantes, vemos que c1    xo   e que
k!
k 0
k
ck   k 1! k , de onde extraímos que c2   2   2 , c3  m3  2 3 e c4  6 4 . Assim a curtose vale
k
6 4
 
2
4

6 , positiva, logo leptocúrtica. Usando o fato de que c  m  3 4 vemos que
4
4

6 4  m4  3 2  4 e extraímos m4  3   2  4 .
Aditividade da distribuição gama:
Sejam x1 , x2 ,
diferentes
, xn n v.a.´s independentes que seguem a distribuição gama de mesmo  mas com
 s e xo s , ou seja, f  xi   Gama  xi  xoi ;i ,   . Então a variável z  x1  x2 
também segue a distribuição com xo  xo1  xo 2 
 xon e   1   2 
 xn
  n e mesmo  . Pelo
teorema
da
 z  t   eix
o1t
convolução
z  t   ei x
o1  xo 2 
 xon t
1  i t  
 1 2   n 
1  i t 
1
eixo 2t 1  i  t 
 2
eixont 1  i  t 
 n
logo
que é a função característica da distribuição gama.
Convergência para a Normal:
Se
  podemos usar o truque do logarítmo para analisar o comportamento assimptótico da
distribuição
gama.
Aplicando
o
logarítmo
na
função
característica
temos:


x 2 x3 x 4
ln   t    ixot   ln 1  i  t  , usando ln(1  x)    x     ... com x  i  t obtemos,
2 3 4


 i t 
ln(1  x)  i t 
até segunda ordem,
2
 2
ln   t   i  xo    t 
2
t
2
ou   t   e
2
 i  t 
i  xo  t 
 2
2
t2
2
2
t 2 . Nesse caso temos então que
que é a função característica de uma


normal com   xo   e  2   2 . Logo para Lim   x  xo ; ,    N x  xo ; ,  2 .
 
Distribuição Chi-quadrado:
Na função Gama vamos fazer  

f  2  x  xo ;  
 x  xo 

2
1
e

x  xo
2
 2
2 2 

e   2 . Nesse caso temos:   v
2
2
e   2 então
H  x  xo  .
Distribuições t-student e F.
Agora suponha a variável

y  x2
onde
x
segue uma normal
y
2
com
N  0,1 . Então y segue a distribuição
1
1  2
2
2
2
fy  y 
y 2e 2 H  y  . Agora a v.a. S  x1  x2 
2
distribuição Gama com
 
f S 2  nnnnnnnn
 xn2
segue a
Suponha que
x
Qual a distribuição de
int  n
x t   e
N   , 
segue uma normal
z  x1  x2 

int 
 2t 2
n
e
2
mudar a v.a. para a média
 xn
t   e
 2t 2
2 .
com x´s iid? A nova função característica será dada por
 t2
2
2
x
cuja função característica vale  x
it 
logo
z

N n , n 
segue uma normal
z 1
  xj .
n n j
Nesse caso
 . Agora vamos
z
f x    nf z  nx  ,
n
ou seja,
2
fx  x  
Chamando

n
einxt e

2 
int  n
 2t 2
2
dt 
  
2

  nt 
n

int  
inxt
2
e
e
d
1

2 
 nt 
s  nt temos que
2
fx  x  
   2

 s
n

i s  
2
eixs e
ds
1

2 
  
 N  ,

n

Distribuição Beta:
Podemos iniciar a distribuição Beta descobrindo quanto vale
n!m! . Usando a forma

z !  2 x 2 z 1 e  x dx podemos reescreever esse produto como:
2
0

n !m !  4  x
0
2 n 1  x 2
e

dx  y
0
2 m 1  y 2
e

dy  4  e

 x2  y 2

x 2 n 1 y 2 m 1dxdy .
0 0
Vamos trocar para coordenadas polares x  r cos , y  r sin  , x 2  y 2  r 2 e dx dy  r dr d .
Temos que integrar apenas no primeiro quadrante, pois x  0 e y  0 , logo 0   
logo:

2
e 0  r  ,


2
n!m!  4  e
r2
r
2 n 1 2 m 1
r
cos
2 n 1
 sin
2 m 1
0 0



  2 n  m 1 1  r 2   2 2 n 1
 r dr d  2 r
e dr  2  cos  sin 2 m 1  d 

 0
  0

2
Ou seja: n!m!   n  m  1!2  cos 2 n 1  sin 2 m 1  d
0
Fazendo t  cos 2  , 1  t  1  cos 2   sin 2  e dt  2sin  cos  d transformamos a integral
acima em

2
n !m!   n  m  1!  cos 2   sin 2  
n
0
1
Então sabemos que:
 t 1  t 
n
0
m
dt 
m
0
 2sin  cos  d    n  m  1!  t n 1  t 
1
 dt    n  m  1!  t n 1  t  dt
n !m !
.
 n  m  1!
1
n 1
A função Beta é definida como B  n, m   t 1  t 

m 1
dt 
0
 n  1! m  1!    n    m 
.
  n  m
 n  m  1!
A distribuição Beta, definida no intervalo 0  x  1 apenas, é dada por:
fbeta  x;  ,   
x 1 1  x 
 1
B  ,  
H  x  H 1  x 
FGM da Beta:
M beta  t  
1
m

1
1
t k k  1
 1
 1
xt  1
e
x
1

x
dx

x x 1  x  dx





B  ,   0
B  ,   k 0 k ! 0
1
1

 B   k, 

 tk
1
t k   k 1
 1
M beta  t  
x
1

x
dx





B  ,   k 0 k !0
B  ,   k !
k 0
1

M beta  t   
k 0
B   k ,   t k
B  ,  
k!
m
0
Daqui
Mk 
extraímos
Mk 
que:
B   k ,  
B  ,  
.
  k  1!   1!     1! , ou seja,
  k    1!   1!   1!
Em
Mk 
termos
Mo 
  1!     1!  1 .
  1   !   1!
2.
M1 
 !     1!  
   !   1!   
3.
M2 
   1
  1!     1! 
    1!   1!        1

 

    1   
2
então  2  M 2   2 será dado por
.
4.
M3 
   1  2 
  2 !     1! 
    2 !   1!
       1    2 
5.
M4 
   1  2   3
  3!     1! 
.
    3!   1!
       1    2     3
Distribuição Logística:
1
F  x;  
1 e

M (t ) 


etx

x  xo

dF  x 
dx

d 
então f  x;  
1  e
dx 
dx  etx F  x 



x  xo


x  xo

1
e 


x  xo 2




1  e  


 t  etx F  x  dx

1
temos:
.
   1
2
    1
 





2
       1              1     
2 
2 
fatoriais
  k  1!     1! .
  k  1   !   1!
1.
então  
dos
.
finalmente
M (t )  e
  t  x  xo 
  
xo t


e
e

x  xo

x  xo



1  e  



2
d
x  xo


e
xot


e 
 t 1
z
1  e 
z
2
dz
1
s
z  ln s dz  ds

M (t )  e

xo t
 t 1
ln s
1  e 
 ln s
0
s
e 
2
1
ds  e xot
s

s t
  s  1
2
ds
0
t
t
1
1
; ds 
1 
dt , s  1 
2
1  t 
1  t 
1  t 
1  t 
t t
1
M (t )  e
xo t
1  t 
t

0
Distribuição
1
1  t 
2
1
1
1  t 
2
dt  e xot  t  t 11 1  t 
 t 11
dt  e xot B 1   t ,1   t 
0
t de Student.
Uma variável aleatória t de Student é dada por uma variável normal cuja variância é igual à recíproca
de uma variável que segue uma distribuição gama. Se a variável x segue uma normal com média nula
mas variância
1
2
  2 x
. A
e
2
  desconhecida então f  x   
2
 segue uma distribuição


1
  1e  H   , então x segue a distribuição:
gama com parâmetros f gama  ; ,    
   


1

1
 
 x2
   1
1
1
1
1

2
2
f  x 
d  e e

d  2 e 




2     0
2     0


 x 2 

2  

1
1  2   x2 
f  x 
1 

2      
2 
Ou seja,
 1  x 
1 

2    
2 
2
modo que f  x  
 
 
1
2 
1
2 
  x 2  d
0 1  2  
z
  x2 
1 

2 


1
2



1
2

1
2
e
  x 2 
 1

2  

, de
1

1
   
2  
 
2  x  2
e dz 
. Para
1 

2    
2 
1
  1  z
2
0
 1 
 1

  x2   2
2
2


.
  v 2 e   chegamos a distribuição t de Student dada por f  x  
1  

    
   
2
A distribuição t de Student não possui função geradora dos momentos mas possui função característica
K  t 
dada por   t  
2

 t

   1
   22
2


2
onde K
2
 x  é a função de Bessel modificada. Note entretanto
que é uma função do módulo de t , não diferenciável, e portanto não pode ser utilizada para cálculo dos
momentos.
Distribuição normal multivariada:
Se as v.a.s correlacionadas seguem uma distribuição normal multivariada queremos mostrar que a
função densidade de probabilidade conjunta é dada por:
f  x   Ae

1
2
 xi  i Vij1  x j   j 
i
j
onde V é a matriz de variância-covariância. O fato de que se trata de
uma matriz definida positiva garante que o expoente será sempre negativo e f caia a zero para grandes
valores de x. Antes de mais nada precisamos encontrar a constante normalizadora A tal que
 Ae

1
2
matriz
 Ae
1

2
  xi  i Vij1  x j   j 
i
dx1dx2
j
V 1 .
Voltando
 

i
j
xi  i Vij1
à
 x j  j 
dx1dx2
dxn  1 . Para realizar essa operação precisamos antes diagnolizar a
distribuição
normal
multivariada
temos
que
a
integral
dxn  1 é complicada por causa dos termos cruzados envolvendo xi
e x j . Então a idéia é diagonalizar e ficar apenas com termos contendo zi2 . Para tanto vamos começar
definindo qi  xi  i e reescrever a integral como A
 e

1
2
 qi Vij1 q j
i
j
dq1dq2
dqn  1 . Agora notamos
 e
que temos A
A e
truque:
1
 qV 1q
2
dqn  1 e diagonalizamos a matriz V-1 no expoente com o seguinte
dq1dq2


1
 qS S V 1S S  q
2
dqn  A e
dq1dq2
para as variáveis giradas, z  S  q , ou seja, zi 



1
 S  q  S V 1S  S  q 
2
 Sq
ij
dq1dq2
dqn  1 . Agora mudamos
. Multiplicando pela inversa de S´ temos que
j
j
q  S z , ou seja, qi   Sij z j de onde tiramos que
j
dqn  det  J  dz1 dz2
matriz S. Sabemos que dq1 dq2
det  S   1
A e
A


então
z2
 2i i
i
dzn  A  e
i
2

dqn  dz1 dz2
dq1 dq2

dz1dz2
1
n
12
qi
 Sij e que a matriz Jacobiana J é a própria
z j

zi2
2 i

dzn . Mas, nesse caso, como J  S e
e
dzn
dzi  A 2i
i

e
a
u 2

integral
fica
na
du  A 2i  1 . Isso significa que
i
onde i são os autovalores de V. Agora, usamos o fato de que a
n
diagonalização de uma matriz preserva o determinante e que, portanto, det V   12
obtemos que A 

2
forma

1
n . Daí
.
n
det V
A distribuição Normal multivariada é dada por:

f x 
e
1
2
 xi  i Vij1  x j   j 
i

j
2


n
det V
e


1
 x    V 1  x   
2
2

n
det V
Para achar a matriz de variância-covariância entre as variáveis x notamos que que as variáveis z´s são


 
independentes, pois f zi , z j  f i  zi  f j z j , seguindo uma normal com esperança nula e variância
i , ou seja, E  zi   0 e E  zi z j   i ij . A relação entre as variáveis z´s e as x´s originais é:
xi  i   Sij z j , de onde tiramos que E  xi   i   Sij E  z j   i e xi  i   Sij z j , logo,
j
j
 xi  i  xk  k    Skl Sij z j zl
j
j
então:
j
E  xi  i  xk  k    Skl Sij E  z j zl   
j
l
j
l
1
Skl Sij jl    j Sij S jk  SDS   V .
j
j
Geração de variáveis correlacionadas – método da decomposição de Cholesky.
Sabemos que a matriz de variância-covariância V é simétrica e definida positiva. Toda matriz dessa
forma pode ser decomposta em uma multiplicação de matrizes triangulares superior e inferior, ou seja,
0
 11 0

 21  22 0
queremos escrever V   onde   
  31  32  33


 11  21  31

0  22  32
  
 0
0  33




 é uma matriz triangular inferior e





 é triangular superior. Sabemos que qualquer matriz dada por M  AA é



simétrica pois M    AA   AA  AA  M . Logo  é uma matriz simétrica. Agora note que
0
 11 0


 22 0
   21
  31  32  33


Percebe-se
do
11 31  V13   31 
 11  21  31

 0  22  32
 0
0  33


processo
V13
V11
que
11 21 11 31
  112
 
2
2
   11 21  21   22
  11 31
 
 
112  V11  11  V11
 212   222  V22   222  V22 
e


.



11 21  V12   21 
V12
V11
e
V122 V11V22  V122
V V V 2

  22  11 22 12 . O
V11
V11
V11
processo pode ser continuado, mas existem pacotes capazes de realizar a decomposição de Cholesky.
Note que é necessário que V seja definida positiva para que as raízes sejam reais.
Agora geramos n v.a.s independentes com esperança nula e variância unitária, i.e., E  xi   0 ;
E  xi x j    ij e com essas variáveis construímos as variáveis z´s dadas por zi    ij x j  zi portanto
j
E  zi    ij E  x j   E  zi   zi . Nesse caso  zi  E  zi    zi  zi    ij x j . Daí extraímos que
j
j
 zk  zk    kl xl
e
 zi  zi  zk  zk     kl  ij x j xl .
l
l
Aplicando a esperança de ambos os
j
lados:
E  zi  zi  zk  zk    kl ij E  x j xl    kl ij jl   ij kj   ij jk    V
l
j
l
j
j
j
Conseguimos então um conjunto de n v.a.s zi com esperança e variância determinadas.
Aspectos fundamentais dessa técnica são: (1) A matriz de partida tem que ser simétrica e definida
positiva; (2) as variáveis independentes devem ter esperança nula e (3) variância igual a 1.