CircuitosEletricosAtivos

Circuitos Elétricos Ativos, análise via transformada de Laplace
Carlos Eduardo de Brito Novaes
[email protected]
18 de maio de 2012
1
Introdução
Utilizando a transformada de Laplace, a modelagem dinâmica de circuitos ativos como compensadores é semelhante à modelagem de circuitos elétricos passivos. Basta substituir as resistências pelas respectivas impedâncias complexas.
Primeiramente apresentamos as configurações usuais com amplificadores operacionais em circuitos de corrente contínua.
Em seguida apresentamos a versão destes circuitos com componentes como capacitores e indutores. Por fim apresentamos
alguns exemplos de projeto e alguns exercícios resolvidos.
Como exemplo, vamos modelar circuitos com amplificadores operacionais, que posteriormente serão utilizados para projetar compensadores. Os compensadores podem ser utilizados para realizar o controle de uma planta1 .
2
Configurações básicas com amplificadores operacionais
Vamos apresentar três configurações com amplificadores operacionais, como exemplo estamos utilizando o componente
CA3140, portanto os valores que forem recomendados são específicos para este componente. Ao ser realizar um projeto,
deve-se verificar a folha de dados para satisfazer as condições de operação dos componentes (por exemplo, limites máximos
e mínimos de tensão e corrente).
A corrente de entrada deste componente é da ordem de 2 pA, enquanto que a corrente máxima de saída é da ordem de
15 mA. Os resistores de realimentação devem levar a uma corrente elétrica na malha que seja muito superior à corrente de
entrada2 , mas com toda certeza, deve ser inferior à corrente máxima que o componente pode fornecer em sua saída.
Além disso, em alguns casos é necessário incluir o ajuste de offset, que é a tensão de equilíbrio da saída. O circuito
necessário para este ajuste esta ilustrado em todas as configurações.
2.1
Amplificador Inversor
Esta configuração é mostrada na figura 1.
1 uma vez que o modelo do sistema é conhecido e de posse das especificações desejadas de desempenho, vamos determinar a a função de transferência de
um compensador para que ao fechar a malha de controle a função de transferência do sistema como um todo atenda às especificações.
2 ao menos 100 vezes maior, de forma que a corrente drenada pela entrada seja desprezível em relação à corrente de realimentação.
1
Figura 1: Esquema de um Amplificador Inversor.
O ganho é dado por:
Vout
Vin
= −
RF
RI
Note que a relação inverte o sinal da tensão elétrica aplicada na entrada, por este motivo a configuração é conhecida como
amplificador inversor. Ainda, se fizermos RI = RF , o ganho será unitário, restando apenas o efeito de inversão. Configurações
com ganho unitário são úteis para se aumentar a corrente proveniente de um sinal cuja impedância de saída seja muito elevada,
por exemplo um sensor.
2.2
Amplificador Não Inversor
Com esta configuração, mostrada na figura 2, podemos obter uma amplificação sem inverter a tensão de entrada.
Figura 2: Esquema de um Amplificador Não Inversor.
2
O ganho é dado por:
Vout
Vin
R2 + R1
R2
=
Se desejarmos ganho unitário, pode-se substituir R1 por um curto circuito e R2 por um circuito aberto, neste caso temos
uma configuração conhecida como seguidor de tensão. Observe pela equação que se R2 for muito maior que R1 o ganho
realmente se aproxima da unidade, o caso limite é quando R1 = 0 (curto circuito) e R2 = ∞ (circuito aberto).
2.3
Amplificador de Instrumentação (Amplificador Subtrator ou Amplificador Diferencial)
Esta terceira configuração é ilustrada na figura 3. A entrada não é referenciada no terra, podemos então realizar operações de
subtração com dois sinais distintos e ainda amplificar esta diferença. Amplificadores subtratores são normalmente utilizados
para recolher o sinal de sensores.
Figura 3: Esquema de um Amplificador Subtrator.
O ganho é dado por:
Vout
Vin
=
RF
RI
+
−
Note entretanto que o sinal Vin é na realidade a subtração de dois sinais distintos Vin = Vin
− Vin
. então:
Vout
=
)
RF ( +
−
Vin − Vin
RI
Este tipo de configuração é muito utilizada quando o sensor se encontra distante3 , pois permite rejeitar o ruído adicionado
+
ao longo do comprimento dos cabos de conexão. Imagine um sensor que produza entre seus dois terminais de saída, Vsensor
e
−
+
−
Vsensor uma tensão Vsensor = Vsensor − Vsensor proporcional à grandeza medida. Ao passar esta tensão por um cabo longo
e sujeito à ruído, de modo geral o ruído sera adicionado de modo semelhante aos dois condutores do cabo, então teremos duas
tensões:
3 Normalmente
o sensor se encontra distante.
3
+
Vin
−
Vin
+
= Vsensor
+ Vruido
−
= Vsensor
+ Vruido
A tensão de saída do amplificador de instrumentação será:
Vout
=
=
=
RF
RI
RF
RI
RF
RI
(
(
(
+
−
Vin
− Vin
)
+
−
Vsensor
+Vruido − Vsensor
−Vruido
+
−
− Vsensor
Vsensor
)
)
Observamos que a saída não será tão afetada pelo ruído de entrada.
3
Compensadores com amplificadores operacionais
Podemos substituir os resistores de realimentação e de entrada por malhas RC, RL ou RLC, neste caso, os ganhos terão
um comportamento dinâmico que poderemos analisar substituindo nas expressões adequadas as resistências por impedâncias
complexas.
Deve-se observar que embora seja teoricamente possível utilizar malhas cuja resistência para corrente contínua seja nula
ou infinita, este tipo de configuração não é recomendável pois no primeiro caso pode significar que a saída do amplificador
operacional será colocada em curto circuito ou, no segundo caso, que não haverá uma corrente elétrica fluindo pela malha de
realimentação. Usualmente utilizam-se associações que garantam um valor adequado para a malha de realimentação.
3.1
3.1.1
Compensador com Amplificador Inversor
Resistor e Capacitor em paralelo
O esquema da figura 4 ilustra um amplificador em configuração inversora, onde os resistores RI e RF foram substituídos por
um circuito RC paralelo, respectivamente RI q CI e RF q CF .
Figura 4: Esquema de um Compensador Inversor com RC paralelo.
4
A função de transferência deste circuito pode ser obtida pela equação de ganho, bastando substituir as resistências originais
pelas impedâncias representadas como funções no domínio de Laplace. Assim:
1
1
1
)
+(
1
RF
sCF
1
=
1
+ sCF
RF
RF
=
1 + sRF CF
De modo semelhante, a impedância da malha de entrada será:
ZF (s) =
ZI (s)
RI
1 + sRI CI
=
Por fim, a função de transferência será:
Vout (s)
Vin (s)
ZF (s)
ZI (s)
RF
1 + sRF CF
= −
RI
1 + sRI CI
RF 1 + sRI CI
= −
RI 1 + sRF CF
RF
1
ou seja, obtemos uma função de transferência cujo ganho estacionário é −
, com um polo em s = −
e um zero
RI
RF CF
1
em s = −
.
RI CI
3.1.2
= −
Resistor e Capacitor em série
Como mencionado anteriormente, este tipo de configuração não assegura uma corrente estacionária na malha de realimentação,
vamos analisar apenas pelo interesse matemático e como forma de exercício. O esquema é ilustrado na figura 5, os resistores
RI e RF foram substituídos por um circuito RC série, respectivamente RI + CI e RF + CF .
Figura 5: Esquema de um Compensador Inversor com RC série.
5
Substituindo as resistências originais pelas impedâncias representadas como funções no domínio de Laplace. Assim:
1
sCF
sRF CF + 1
sCF
ZF (s) =
RF +
=
De modo semelhante, a impedância da malha de entrada será:
ZI (s)
sRI CI + 1
sCI
=
Por fim, a função de transferência será:
Vout (s)
Vin (s)
ZF (s)
ZI (s)
sRF CF + 1
sCF
= −
sRI CI + 1
sCI
sRF CF + 1 sCI
= −
sRI CI + 1 sCF
sRF CF + 1 CI
= −
sRI CI + 1 CF
= −
em teoria, obtemos uma função de transferência cujo ganho estacionário é −
em s = −
3.1.3
1
.
RF CF
CI
1
, com um polo em s = −
e um zero
CF
RI CI
Resistor e Capacitor em série e paralelo
Na configuração anterior, adicionando resistores em paralelo com os capacitores garantimos uma corrente de repouso na
malha de realimentação. O esquema é ilustrado na figura 6, os resistores RI e RF foram substituídos por um circuito RC série,
respectivamente RI1 + CI q RI2 e RF + CF q RF 2 .
Figura 6: Esquema de um Compensador Inversor com RC série e paralelo.
6
Substituindo as resistências originais pelas impedâncias representadas como funções no domínio de Laplace. Assim:
ZF (s)
1
1
1
)
+(
1
RF
sCF
RF 2
= RF 1 +
1 + sRF 2 CF
RF 1 (1 + sRF 2 CF ) + RF 2
=
1 + sRF 2 CF
RF 1 + sRF 1 RF 2 CF + RF 2
=
1 + sRF 2 CF
=
RF 1 +
De modo semelhante, a impedância da malha de entrada será:
ZI (s) =
RI1 + sRI1 RI2 CI + RI2
1 + sRI2 CI
Por fim, a função de transferência será:
Vout (s)
Vin (s)
ZF (s)
ZI (s)
RF 1 + sRF 1 RF 2 CF + RF 2
1 + sRF 2 CF
−
RI1 + sRI1 RI2 CI + RI2
1 + sRI2 CI
1
RF 1 + sRF 1 RF 2 CF + RF 2
1 + sRF 2 CF
−
×
1
RI1 + sRI1 RI2 CI + RI2
1 + sRI2 CI
1 + sRI2 CI
RF 1 + RF 2 + sRF 1 RF 2 CF
−
×
1 + sRF 2 CF
RI1 + RI2 + sRI1 RI2 CI
RF 1 + RF 2
RF 1 RF 2 CF
+s
1 + sRI2 CI
RF 1 + RF 2
RF 1 + RF 2
RF 1 + RF 2
−
×
×
RI1 + RI2
RI1 RI2 CI
1 + sRF 2 CF
RI1 + RI2
+s
RI1 + RI2
RI1 + RI2
RF 1 RF 2
1+s
CF
RF 1 + RF 2
1 + sRI2 CI
RF 1 + RF 2
−
×
×
RI1 RI2
RI1 + RI2
1 + sRF 2 CF
1+s
CI
RI1 + RI2
= −
=
=
=
=
=
RF 1 + RF 2
1
, com dois polos em s = −
es=
RI1 + RI2
RF 2 CF
RI1 + RI2
1
RF 1 + RF 2
−
, e com dois zeros em s = −
es=−
.
RI1 RI2 CI
RI2 CI
RF 1 RF 2 CF
Este tipo de compensador é chamado de “lead-lag” pois possui uma rede de avanço de fase e outra rede de atraso de fase.
obtemos uma função de transferência com ganho em repouso −
3.1.4
Resistor e Indutor em série
De modo semelhante, pode-se equacionar a função de transferência para um circuito com indutores. Ilustramos o esquema na
figura 7.
7
Figura 7: Esquema de um Compensador Inversor com RL série.
Substituindo as resistências originais pelas impedâncias representadas como funções no domínio de Laplace. Assim:
ZF (s) =
RF + sLF
De modo semelhante, a impedância da malha de entrada será:
ZI (s) =
RI + sLI
Por fim, a função de transferência será:
Vout (s)
Vin (s)
ZF (s)
ZI (s)
RF + sLF
= −
RI + sLI
LF
1+s
RF
RF
= −
LI
RI
1+s
RI
= −
Obtivemos então uma função de transferência com ganho em repouso igual a −
zero em s = −
3.2
3.2.1
RF
.
LF
RF
RI
, com um polo em s = −
e um
RI
LI
Compensador com Amplificador Não Inversor
Resistor e capacitor em paralelo
O esquema da figura 8 ilustra um amplificador em configuração não inversora, onde os resistores R1 e R2 foram substituídos
por um circuito RC paralelo, respectivamente R1 q C1 e R2 q C2 .
8
Figura 8: Esquema de um Compensador Não Inversor com RC paralelo.
A função de transferência deste circuito pode ser obtida pela equação de ganho, bastando substituir as resistências originais
pelas impedâncias representadas como funções no domínio de Laplace. Assim:
Z1 (s)
=
=
=
1
1
1
)
+(
1
R1
sC1
1
1
+ sC1
R1
R1
1 + sR1 C1
De modo semelhante, a impedância da malha de entrada será:
R2
1 + sR2 C2
Z2 (s) =
Por fim, a função de transferência será:
9
Vout (s)
Vin (s)
=
=
=
=
=
Z1 (s) + Z2 (s)
Z2 (s)
R1
R2
+
1 + sR1 C1
1 + sR2 C2
R2
1 + sR2 C2
R1 (1 + sR2 C2 ) + R2 (1 + sR1 C1 )
(1 + sR2 C2 ) (1 + sR1 C1 )
R2
1 + sR2 C2
(1 + sR2 C2 ) (R1 (1 + sR2 C2 ) + R2 (1 + sR1 C1 ))
R2 (1 + sR2 C2 ) (1 + sR1 C1 )
(R1 + R2 ) + s (R1 R2 C2 + R1 R2 C1 )
R2 (1 + sR1 C1 )
Com um artifício matemático, isolamos o ganho em repouso do sistema:
Vout (s)
Vin (s)
(R1 R2 C2 + R1 R2 C1 )
(R1 + R2 )
R2 (1 + sR1 C1 )
R1 R2 (C2 + C1 )
1+s
R1 + R2
R1 + R2
R2
1 + sR1 C1
(R1 + R2 ) + (R1 + R2 ) s
=
=
ou seja, obtemos uma função de transferência cujo ganho estacionário é
zero em s = −
4
R1 + R2
.
R1 R2 (C2 + C1 )
R1 + R2
1
, com um polo em s = −
e um
R2
R1 C1
Exemplos de Projeto
4.1
Compensador lag com configuração inversora
Suponhamos que seja necessário projetar um compensador inversor com ganho −10, um polo em s = −2 e um zero em
s = −10. Este tipo de compensador é chamado “compensador lag” ou “compensador por atraso de fase” pois o zero4 é mais
“rápido” que o polo.
Podemos adotar a configuração de compensador com amplificador inversor com um circuito RC paralelo, e se adotarmos
ainda o amplificador operacional CA3140, já temos uma faixa de valores aceitáveis para o resistor RF .
As equações, demonstradas anteriormente são:
Vout (s)
Vin (s)
= −
RF 1 + sRI CI
RI 1 + sRF CF
Se escolhermos RF = 100 K Ohms, imediatamente fixamos RI para um ganho −10:
−10
RI
4o
RF
RI
10000
= −
RI
10000
=
10
=
−
zero do sistema esta mais distante do zero, portanto seu efeito é mais rápido que o efeito do polo.
10
Portanto, RI = 10 K Ohms.
Resta-nos agora determinar os capacitores CI e CF . Para o zero em s = −10, o valor do capacitor CI será:
1+s
1
10
s
10
1
10
1
10 × 10000
= 1 + sRI CI
=
1 + s × 10000 × CI
=
s × 10000 × CI
= 10000 × CI
=
CI
1
Portanto, tem-se CI =
F ou CI = 10 µF.
100000
De modo semelhante, vamos calcular CF para que o polo esteja localizado em s = −2.
1+s
1
2
s
2
1
2
1
2 × 100000
Portanto, tem-se CI =
4.2
= 1 + sRF CF
= 1 + s × 100000 × CF
= s × 100000 × CF
= 100000 × CF
= CF
1
F ou CI = 5 µF.
200000
Compensador lead com configuração inversora
De modo semelhante ao exemplo anterior, desejamos projetar um compensador com ganho em repouso −10, zero em s = −2
e polo em s = −10. Trata-se de um compensador do tipo “lead” ou “avanço de fase”, pois o polo é mais “rápido” que o zero.
Vamos utilizar a mesma configuração do exemplo anterior, inclusive, como o ganho em repouso é o mesmo, podemos
adotar os mesmos valores de resistores, ou seja, RF = 100 K Ohms e RI = 10 K Ohms. A diferença é que os valores
desejados para o polo e para o zero foram trocados, assim, resta-nos calcular os valores dos capacitores.
Para o zero em s = −2, o valor do capacitor CI será:
1+s
1
2
s
2
1
2
1
2 × 10000
= 1 + sRI CI
= 1 + s × 10000 × CI
=
s × 10000 × CI
= 10000 × CI
=
CI
1
Portanto, tem-se CI =
F ou CI = 50 µF.
20000
De modo semelhante, vamos calcular CF para que o polo esteja localizado em s = −10.
11
1+s
1
10
s
10
1
10
1
10 × 100000
Portanto, tem-se CI =
4.3
= 1 + sRF CF
= 1 + s × 100000 × CF
= s × 100000 × CF
= 100000 × CF
= CF
1
F ou CI = 1 µF.
1.000.000
Compensador lag com configuração não inversora
Vamos refazer o projeto em uma configuração não inversora, com ganho em repouso igual a 10, e repetindo um polo em
s = −2 e um zero em s = −10. A equação da função de transferência do amplificador não inversor, deduzida anteriormente,
é:
Vout (s)
Vin (s)
=
R1 + R2
R2
1+s
R1 R2 (C2 + C1 )
R1 + R2
1 + sR1 C1
Como de costume, vamos calcular os resistores para assegurar um ganho igual a 10. Assumindo R1 = 100 K Ohms,
tem-se:
R1 + R2
R2
100000 + R2
=
R2
= 100000 + R2
= 100000
10 =
10 × R2
10 × R2 − R2
9 × R2
R2
R2
= 100000
100000
=
9
u 11111
Ou seja, devemos escolher R2 aproximadamente igual a 11.1 K Ohms.
Vamos agora determinar o polo do sistema pois este depende apenas de C1 :
1+
s
2
s
2
1
2
1
2
1
2 × 100000
Encontramos então que o valor de C1 =
= 1 + sR1 C1
= sR1 C1
= R1 C1
= 100000C1
= C1
1
F ou C1 = 5 µF.
200000
12
Resta apenas calcular o valor de C2 para obter o zero especificado:
1+
s
10
s
10
1
10
=
=
1
10
=
1
10
=
1
10
=
Coincidentemente, o valor calculado foi C2 =
4.4
=
1
10
1
100000
1
1
−
100000 200000
1
200000
R1 R2 (C2 + C1 )
R1 + R2
R1 R2 (C2 + C1 )
s
R1 + R2
R1 R2 (C2 + C1 )
R1 + R2
(
)
100000
1
100000 ×
C2 +
9
200000
100000
100000 +
( 9
)
100000
1
100000 ×
C2 +
9
200000
(
)
1
100000 1 +
9
(
)
100000
1
C2 +
9
200000
10
9
(
)
1
10000 C2 +
200000
1
C2 +
200000
= 1+s
=
= C2
= C2
1
F ou C2 = 5 µF.
200000
Compensador lead-lag com configuração inversora
Projete um compensador do tipo “lead-lag” com ganho em repouso de −10, polos em s = −2 e s = −5, e zeros em s = −4
e s = −10.
Vamos utilizar a estrutura da figura 6, mas como as equações são mais complicadas, devemos estudar com mais atenção
antes de fazer nossas escolhas. É possível que o circuito não seja realizável para qualquer valor dos componentes e, em
alguns casos pode ser necessário utilizar dois compensadores separados. A equação da função de transferência, calculada
anteriormente, é:
Vout (s)
Vin (s)
=
−
RF 1 + RF 2
1 + sRI2 CI
×
RI1 + RI2
1 + sRF 2 CF
RF 1 RF 2
CF
RF 1 + RF 2
×
RI1 RI2
1+s
CI
RI1 + RI2
1+s
Inicialmente, verificamos que o ganho pedido é −10, significando que RF 1 +RF 2 deve ser 10 vezes maior que RI1 +RI2 .
RF 1 + RF 2
=
13
10 (RI1 + RI2 )
Escolhemos então, para a malha de realimentação, RF 1 + RF 2 = 100 K Ohms. Assim, RI1 + RI2 = 10 K Ohms. Vamos
escolher os polos e zeros, mas é possível que a equação não tenha solução, neste caso podemos tentar escolher de outra forma5 .
1
RI2 CI
1
4
=
4
= RI2 CI
(1)
,
RF 1 + RF 2
= 10
RF 1 RF 2 CF
100000
= 10
RF 1 RF 2 CF
10000 = RF 1 RF 2 CF
(2)
,
1
RF 2 CF
1
2
=
2
= RF 2 CF
(3)
e
RI1 + RI2
= 5
RI1 RI2 CI
10000
= 5
RI1 RI2 CI
2000 = RI1 RI2 CI
(4)
Substituindo (1) em (2)
2000
= RI1
8000
= RI1
1
4
e consequentemente:
RI1 + RI2
RI2
RI2
RI2
= 10000
= 10000 − RI1
= 10000 − 8000
= 2000
substituindo estes valores na equação (1):
1
4
1
4
CI
5A
= RI2 CI
=
2000CI
=
1
8000
escolha apresentada leva é possível de ser implementada, mas se tivéssemos escolhido
com resistores negativos. Neste caso a alternativa seria tentar trocar os valores.
14
1
RF 1 + RF 2
= 10 e
= 4, obteríamos uma solução
RI2 CI
RF 1 RF 2 CF
confirmando pela equação (4):
2000
= RI1 RI2 CI
2000
= 8000 × 2000 ×
2000
= 2000
1
8000
E agora, substituindo (3) em (2)
10000
= RF 1
20000
= RF 1
1
2
e consequentemente:
RF 1 + RF 2
= 100000
RF 2
RF 2
= 100000 − RF 1
= 100000 − 20000
RF 2
= 80000
substituindo estes valores na equação (3):
1
2
1
2
= RF 2 CF
CF
=
80000CF
=
1
160000
confirmando pela equação (2):
10000 =
RF 1 RF 2 CF
10000 = 20000 × 80000 ×
1
160000
10000 = 10000
Sendo assim, é possível construir este compensador se escolhermos os valores:
CF
RF 1
RF 2
CI
RI1
RI2
1
= 6, 25 µF
160000
= 20 K Ohms
= 80 K Ohms
1
= 125 µF
=
8000
= 8 K Ohms
= 2 K Ohms
=
15
5
5.1
Exercícios resolvidos
Determine a função de transferência para o circuito da figura 4, onde:
RF
CF
= 1 M Ohms
= 1 µF
RI
CI
= 47 K Ohms
= 0, 47 µF
Resolução:
Trata-se de um amplificador inversor, a função de transferência encontrada anteriormente é:
Vout (s)
Vin (s)
= −
RF 1 + sRI CI
RI 1 + sRF CF
Substituindo os valores:
Vout (s)
Vin (s)
=
=
=
1000000 1 + s × 47000 × 0, 47 × 10−6
47000 1 + s × 1000000 × 1 × 10−6
1000 1 + s × 47 × 0, 47 × 10−3
−
47
1+s
1000 1 + 0, 02209s
−
47
1+s
−
1000
Ou seja, o ganho em repouso é igual a −
, aproximadamente 21, 27, existe um polo em s = −1 e um zero em
47
1
s=−
u −45, 26.
0, 02209
5.2
Determine a função de transferência para o circuito da figura 8, onde:
R1
=
1 M Ohms
C1
R2
=
=
1 µF
47 K Ohms
C2
= 0, 47 µF
Resolução:
Trata-se de um amplificador não inversor, a função de transferência encontrada anteriormente é:
Vout (s)
Vin (s)
=
R1 + R2
R2
1+s
Substituindo os valores:
16
R1 R2 (C2 + C1 )
R1 + R2
1 + sR1 C1
Vout (s)
Vin (s)
=
=
=
=
(
)
1000000 × 47000 0, 47 × 10−6 + 1 × 10−6
1000000 + 47000 1 + s
1000000 + 47000
47000
1 + s1000000 × 1 × 10−6
47000000000 × (1, 47) × 10−6
1
+
s
1047000
1047000
47000
1 + s × 1000000 × 10−6
47 × (1, 47)
1047 1 + s
1047
47
1+s
69, 09
1047 1 + s 1047
47
1+s
Ou seja, o ganho em repouso é igual a
5.3
1047
1047
u 22, 27, existe um polo em s = −1 e um zero em s = −
u −15, 15.
47
69, 09
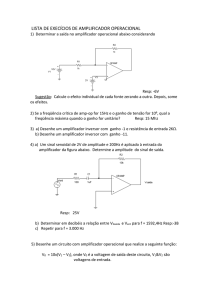
Determine a função de transferência para o circuito da figura 9 para valores arbitrários de
RI , RF , LF e CF . Em seguida obtenha a função de transferência para os valores:
RF
CF
= 100 K Ohms
= 100 µF
LF
RI
= 10 mH
= 10 K Ohms
Figura 9: Esquema do Exercício 5.3 .
Resolução:
Trata-se de um amplificador não inversor, mas neste caso, ainda não calculamos a função de transferência. As impedâncias
ZI e ZF serão:
17
ZI (s) =
ZF (s) =
=
=
=
=
RI
1
1
+
RF
1
LF s +
1
CF s
1
1
1
+
RF
LF CF s2 + 1
CF s
1
CF s
1
+
RF
LF CF s2 + 1
1
LF CF s2 + 1 + RF CF s
LF RF CF s2 + RF
LF RF CF s2 + RF
LF CF s2 + RF CF s + 1
Então, a função de transferência será:
Vout (s)
Vin (s)
=
=
=
=
LF RF CF s2 + RF
L C s2 + RF CF s + 1
− F F
RI
LF RF CF s2 + RF
−
LF RI CF s2 + RI RF CF s + RI
RF
LF CF s2 + 1
−
RI LF CF s2 + RF CF s + 1
1
s2 +
RF
LF CF
−
1
RI 2 RF
s +
s+
LF
LF CF
RF
E esta é a função de transferência do circuito da figura 9. Observamos que o ganho em repouso é −
, existe um par de
RI
√
√
2
1
RF
RF
4
zeros complexos conjugados em s = 0 ± j
e polos em s = −
±
−
. Se o radical for negativo, os
2
LF CF
LF
LF
LF CF
polos serão também complexos conjugados.
Substituindo os valores dos componentes na equação obtida:
Vout (s)
Vin (s)
=
=
=
1
10 ×
× 100 × 10−6
100000
1
s2 +
s+
−3
−3
10 × 10
10 × 10 × 100 × 10−6
9
10
s2 +
10
× 100
−10
109
s2 + 10000 × 103 s +
10 × 100
s2 + 106
−10 2
s + 107 s + 106
100000
−
10000
s2 +
18
10−3
Posteriormente, quando estudarmos a resposta temporal, verificaremos que esta função de transferência apresenta uma
√
rad
107
frequência natural ωn = 106 = 1000
e um coeficiente de amortecimento ξ =
= 5000.
seg
2 × 1000
19