x - Dores

2010 / 2011 / 2012 / 2013
8%
Matemática Básica (Conceitos do Ensino Fund. Questões iniciais)
8%
Geometria Plana e Espacial
20%
4%
Geometria Analítica
4%
Exponenciais e Logarítmos
Sequências, PA e PG
Trigonometria e Números Complexos
Matrizes, Determinantes e Sistemas Lineares
12%
24%
Probabilidade e Análise Combinatória
8%
Funções e Polinõmios
12%
Geometria
Mathematikós
"Aquele que aprende(mathematikós)
decodificando(máthema) os traçados (curvarum) da
natureza (phýsis)".
360°
360 significa 360
partes!
Os babilônios (2000 a.C.), por usarem numeração na base
60 e conhecerem o número PI como 3, dividiram a
circunferência em 360 partes (gradus
(gradus)
gradus), e cada parte foi
dividida em 60 partes menores , os minutos (minuta: parte
menor) que por sua vez, foram divididas em outras 60
partes secundares (secundus): um grau tem 60 minutos, e
um minuto, 60 segundos.
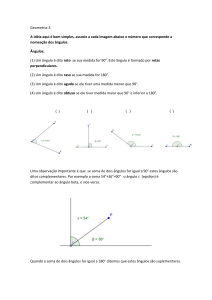
Ângulos
• Agudos:
(do latin, angulus: pequena dobra)
β
0º < β < 90º
• Obtusos:
α
90º < α < 180º
• Reto:
Igual à 90°
90°
•Raso:
α
a) ÂNGULOS ADJACENTES
α
β
Um lado em comum.
ÂNGULOS OPOSTOS PELO VÉRTICE
α
α
São congruentes
a) ÂNGULOS COMPLEMENTARES
α + β = 90º
α
β
b) ÂNGULOS SUPLEMENTARES
θ + δ = 180º
θ
δ
(ENEM 2009) Rotas aéreas são como pontes que ligam cidades, estados ou
países. O mapa a seguir mostra os estados brasileiros e a localização de algumas
capitais identificadas pelos números. Considere que a direção seguida por um
avião AI que partiu de Brasília – DF, sem escalas, para Belém, no Pará, seja um
segmento de reta com extremidades em DF e em 4.
Suponha que um passageiro de nome Carlos pegou um avião AII, que seguiu a direção
que forma um ângulo de 135° graus no sentido horário com a rota Brasília – Belém e
pousou em alguma das capitais brasileiras. Ao desembarcar, Carlos fez uma conexão e
embarcou em um avião AIII, que seguiu a direção que forma um ângulo reto, no
sentido anti-horário, com a direção seguida pelo avião AII ao partir de Brasília-DF.
Considerando que a direção seguida por um avião é sempre dada pela semirreta com
origem na cidade de partida e que passa pela cidade destino do avião, pela descrição
dada, o passageiro Carlos fez uma conexão em:
Belo Horizonte, e em seguida embarcou
para Salvador.
ÂNGULOS ENTRE AS RETAS PARALELAS
E UMA RETA SECANTE
Sabendo que r//s, dê a medida do ângulo indicado por
“x”:
40°
•140°
•130°
•40°
•50°
•n.d.a
x
Qual é o valor de x representado na figura abaixo?
6x+ 15°
2x+ 5°
Ângulos
Ângulos
Ângulos
Ângulos
Ângulos
correspondentes: a e e, d e h, b e f, c e g Congruentes
colaterais externos: a e h, b e g Suplementares
colaterais internos: e e d, c e f Suplementares
alternos externos: a e g, b e h Congruentes
alternos internos: d e f, c e e Congruentes
Internos
O ângulo obtuso de um paralelogramo mede
120°. A medida do ângulo agudo desse
paralelogramo é
a)
b)
c)
d)
e)
90°
80°
70°
60°
50°
Há mais de 2200 anos, Eratóstenes teve a ideia de realizar esse cálculo a partir de um
fenômeno que era uma curiosidade popular na cidade de Siena, no Egito antigo. No solstício de
verão do Hemisfério Norte, ao meio-dia, o Sol ficava exatamente na vertical e sua luz se refletia
na água de um poço profundo sem deixar sombras nas paredes. Porém, em Alexandria, uma
cidade situada mais ao norte, naquele mesmo instante, o fenômeno não ocorria.
Primeiro, ele calculou a circunferência da Terra.
Luz do sol
Luz do sol
Alexandria
Luz do sol
Luz do sol
Siena
• A distância entre as cidades foi “arredondada” para 800km.
• O ângulo formado pela reta(luz do sol) com a vertical em Alexandria foi de 7,2°.
• A reta(luz do sol) em Siena é paralela, por isso, temos também 7,2° (ângulos
correspondentes).
7,2°
Luz do sol
7,2°
• Se um arco de 7,2° corresponde, aproximadamente 800km, quantos
km corresponderiam 360° (uma volta completa)?
7,2°
800
360°
x
, =
. =
, = km
Eratóstenes teve um erro de
arredondamento de
aproximadamente 76km porque
na época havia uma grande
imprecisão entre a distância
Alexandria e Siena.
Teorema:
A soma dos ângulos internos de um triângulo é sempre igual a 180°.
Um triângulo pode ter:
a)
b)
c)
d)
e)
Passa de 180°
Dois ângulos retos e um agudo.
Dois ângulos obtusos e um agudo. Passa de 180°
Dois ângulos agudos e um obtuso.
Um ângulo reto e um obtuso. Passa de 180°
Dois ângulos obtusos e dois ângulos agudos. Passa de 180°
Na figura adiante, as retas r e s são paralelas, o ângulo 1 mede 45° e
o ângulo 2 mede 55°. A medida, em graus, do ângulo 3 é:
45°
r
45°
1
3
x
55°
2
45°
s
(FURG) Na figura abaixo, as retas r e s são paralelas.
A medida do ângulo y, em graus é:
As retas paralelas r e s são cortadas pela reta t como mostra a figura
abaixo. A medida do ângulo é:
a)
b)
c)
d)
e)
120°.
100°.
140°.
130°.
110°.
Qual é a soma dos ângulos internos de um polígono?
2 x180° = 360°
4 x180° = 720°
3 x180° = 540°
5 x180° = 900°
3 x180° = 540°
6 x180° = 1080°
Qual é a medida de um dos ângulos internos de um polígono regular?
360°
720°
=120°
= 90°
°
540°
= 108°
1080°
8
(UERJ) Se um polígono tem todos os lados iguais, então todos os
seus ângulos internos são iguais. Para mostrar que esta proposição
é falsa, pode-se usar como exemplo a figura denominada:
a) losango
b) trapézio
c) retângulo
d) quadrado
e) hexágono
(Unifesp) Pentágonos regulares congruentes podem ser conectados, lado a lado,
formando uma estrela de cinco pontas, conforme destacado na figura:
Nestas condições, o ângulo š mede
a) 108°.
b) 72°.
c) 54°.
d) 36°.
e) 18°.
540°
= 108°
Qual é a medida de um dos ângulos externos de um polígono regular?
108°
90°
°
Ângulo Externo:
onde “n” é o número de vértices. Que é igual ao número de lados.
90°
O polígono que dá forma a essa calçada é
invariante por rotações, em torno de seu
centro, de
a) 45°
b) 60°
c) 90°
d) 120°
e) 180°
45°
90°
180°
120°
60°
120°
120°
120°
°
128, 57°
(UFRGS) Um raio de luz é refletido por três espelhos planos, dois dos quais são
paralelos, como mostra a figura. Lembrando que o raio de luz é refletido por um
espelho segundo seu ângulo de incidência, ou seja, o ângulo de reflexão é igual ao
ângulo de incidência, o valor de é, em graus
(UFRGS – 2012) Assinale a alternativa que apresenta
corretamente os valores, na mesma unidade de medida, que
podem representar as medidas dos lados de um triângulo.
a) 1 – 2 – 4.
b) 3 – 2 – 6.
c) 8 – 4 – 3.
d) 3 – 9 – 4.
e) 6 – 4 – 5.
8
4
10
5
16
4
12
10
2
5
3
3
3
O desenho ao lado foi feito numa malha formada por
quadrados idênticos, e a árvore menor foi obtida a partir
de uma redução da árvore maior em que foram mantidas
as proporções originais. Se a altura da árvore maior é
igual a 60, então a altura da árvore menor vale:
B
A) 30.
B) 20.
C) 15.
D) 12.
O maior tem o triplo da altura do menor!
3-(ENEM 2009) A figura a seguir mostra
as medidas reais de uma aeronave que
será fabricada para utilização por
companhias de transporte aéreo. Um
engenheiro precisa fazer o desenho
desse avião em escala de 1:150.
1 m equivale a 100cm
Escala:
2850cm
1m
1
150
Reduzir 150 vezes!
3600cm
3600 !
120
=
= 24cm
150
5
2850
150
=
57
= 19cm
3
26cm
19 cm
21cm
24cm
(ENEM 2011) Para uma atividade realizada no laboratório de matemática, um aluno precisa
construir uma maquete da quadra de esportes da escola que tem 28 m de comprimento por
12 m de largura. A maquete deverá ser construída na escala de 1 : 250.
Que medidas de comprimento e largura, em cm, o aluno utilizará na construção da maquete?
a) 4,8 e 11,2
b) 7,0 e 3,0
c) 11,2 e 4,8
Escala:
Reduzir 250 vezes!
d) 28,0 e 12,0
e) 30,0 e 70,0
1
250
Atenção!!
12m são 1200cm.
1m são 100cm.
28m são 2800cm.
2800 280
=
= 11,2
250
25
1200
250
=
120
25
=
4,8
Teorema de Tales
Dados: um feixe de retas paralelas e retas transversais,
a razão entre as medidas dos segmentos quaisquer de uma das
transversais é igual à razão entre as medidas dos segmentos
correspondentes de outra.
A
B
C
D
A’
AB
A' B '
=
CD C ' D '
B’
C’
D’
As medidas dos segmentos
correspondentes nas transversais são
diretamente proporcionais
25m
20m
x
30m
Observe a figura.
O homem tem 1,80m de altura e sua sombra mede 2m. Se a sombra
da árvore mede 5m, a altura da árvore, em metros, é:
A)6,3
alturinha
Altura
B)5,7
=
C)4,5 sombrinha sombra
D)3,6
x
1,80 x
=
2
5
0.90 x
=
1
5
-Não sei, não.
1,80m---------------------2m
0,90m---------------------1m
x---------------------5m
x---------------------5m
X=4,5
(UFPI) A área do quadrado ABCD inscrito no triângulo
retângulo DEF, abaixo, é, em cm2:
A)42,25
B)36
C)46,24
D)39,32
E)49
1,60
1,10
=
0,50
(UFRGS) Nos triângulos da figura, os lados de comprimento x e 10
são paralelos. O valor de x é
(ENEM 2009)A rampa de um hospital tem na sua parte mais elevada uma
altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se
deslocou 3,2 metros e alcançou uma altura de 0,8 metros. A distância em
metros que o paciente ainda deve caminhar para atingir o ponto mais alto da
rampa é:
2,2m
0,8m
Pequeno
Grande
3,2
3,2+x
=
0,8
2,2
3,2
0,8
3,2+x
2,2
(UFRGS) Na figura abaixo AB, CD e EF são paralelos AB e CD medem,
respectivamente, 10 cm e 5 cm.
O comprimento de EF, em cm, é
5/3
2
3
10/3
4
-Não sei, não.
B
D
10 cm
5 cm
F
x
a)
b)
c)
d)
e)
A
E
C
B
10 cm
D
x
5 cm
F
A
10-x
=
10
x
5
50-5x=10x
50=15x
E
C
ÂNGULOS DOS LADOS PERPENDICULARES
α
α + β = 180°
β
(UFRGS) Na figura abaixo AC = 5, BC = 6 e DE = 3.
A área do triângulo ADE é
A)
15/8.
B)
15/4.
C)
15/2.
D)
10.
E)
15.
(UFRGS) Um retângulo cujo lado maior é igual a 1 e cujo lado menor é igual a
x, é cortado por uma linha, como na figura, formando um quadrado de lado x
e um retângulo semelhante ao anterior.
O valor de x é
a) 1 – x.
b) 1 – 5.
c) 5 – 1.
– 1.
d)
%
e) 2 5 - 1.
x
1
(UCS) Um retângulo cujo comprimento mede C e cuja altura mede l é um retângulo
' (
áureo, se e somente se ( =
')(
Dessa igualdade, chamada proporção áurea, surgiu um critério estético muito usado por
artistas dede o século V a. C. Por exemplo, têm-se indícios de que o templo grego Parthenon
(erguido entre 447 e 432 a.C.) teve seu projeto baseado no retângulo áureo.
Se, na proporção áurea, for considerada unitária a altura l, obtém-se uma equação cuja raiz
positiva, chamada número de ouro, é
a)
b)
c)
d)
e)
(1+ √2)/2
(1+ √7)/2
(1+ √3)/2
(1+ √6)/2
(1+ √5)/2
O Número
• Existem diversas
definições matemáticas
para FI, ao lado as mais
conhecidas.
Uma Aproximação Melhor
1.6180339887 4989484820 4586834365 6381177203 0917980576
2862135448 6227052604 6281890244 9707207204 1893911374
8475408807 5386891752 1266338622 2353693179 3180060766
7263544333 8908659593 9582905638 3226613199 2829026788
0675208766 8925017116 9620703222 1043216269 5486262963
1361443814 9758701220 3408058879 5445474924 6185695364
8644492410 4432077134 4947049565 8467885098 7433944221
2544877066 4780915884 6074998871 2400765217 0575179788
3416625624 9407589069 7040002812 1042762177 1117778053
1531714101 1704666599 1466979873 1761356006 7087480710
1317952368 9427521948 4353056783 0022878569 9782977834
7845878228 9110976250 0302696156 1700250464 3382437764
8610283831 2683303724 2926752631 1653392473 1671112115
8818638513 3162038400 5222165791 2866752946 5490681131
7159934323 5973494985 0904094762 1322298101 7261070596
(UFRGS – 2012) O conjunto solução da equação1
igual ao conjunto solução da equação.
a)
b)
c)
d)
e)
x² - x – 1 =0
x² + x – 1 =0
– x² -x + 1 =0
x² + x + 1 =0
– x² + x – 1 =0
+
,
.
,-/
= x, com x ≠ 0 e x ≠ -1, é
O corpo de diversos animais também apresenta a razão áurea:
O abacaxi também esconde a razão
áurea no número de segmentos
seguindo cada uma de espirais,
atenção na animação ao lado.
Cavala
Truta
Sardinha
Perca
Jennifer Aniston
Angelina Jolie
O FI na Arquitetura (Grécia)
Os gregos já usavam
o retângulo áureo
em suas construções
mais importantes, o
Partenon é um
exemplo claro disso.
O FI na Arquitetura (Paris)
Encontramos a razão áurea em
diversas proporções da igreja de
Notre-Dame, em Paris.
O FI na Arquitetura (Egito)
Encontramos a razão áurea nas pirâmides do Egito.
O FI na Arquitetura (Canadá)
No Canadá encontramos
o FI na torre CN, em
Toronto.
O FI na Fotografia
Volkswagen Beetle - Jay Mays, Freeman Thomas, Peter Schreyer, 1997
O FI na Música
• O tempo de uma música pode ser visto como
uma razão, por exemplo a razão entre os
tempos de batidas de bumbo e caixa de uma
bateria por exemplo.
• Em algumas de suas sinfonias Ludwig Van
(Beethoven para os íntimos) usou a razão áurea
na marcação do tempo. Encontramos a razão
em sua quinta e nona sinfonias.
• Max Roach, baterista de Jazz também usou FI
em alguns de seus solos.
Subdivisão de um retângulo √3
Subdivida o retângulo √3 em três partes, para
criar três retângulos menores que serão
proporcionais. Subdivida-os novamente em
três partes. Este processo pode ser repetido
indefinidamente, em uma série infinita de
retângulos √3.
Construção de um hexágono
Pode-se construir um hexágono, a partir de um
retângulo. Basta girar o retângulo em torno do
seu eixo, até que as arestas se encontrem.
O retângulo √3 tem a propriedade de permitir a
construção de um prisma hexagonal regular.
se, na natureza, como cristais
Este hexágono apresenta-se,
de neve, favos de mel e em muitas outras formas naturais.
Hipotenusa
Cateto
a²=b²+c²
a
b
Cateto c
hipotenusa²=cateto²+outro cateto²
No triângulo retângulo, o quadrado da
hipotenusa é igual à soma dos
quadrados dos catetos.
13m
x
12m
13² = 12² + X²
169 = 144 + X²
169 - 144 = X²
25 = X²
X=5
17m
x
15m
x²
= 1² + 1²
X²
= 1 + 1
X² = 2
X = 2
17² = 15² + X²
289 = 225 + X²
289 - 225 = X²
64 = X²
X=8
x
1m
1m
3cm
4cm
0,3cm
0,4cm
16cm
6cm
8cm
9cm
15cm
12cm
25cm
6) (UFRGS) Uma torre vertical é presa por cabos de aço fixos
no chão, em um terreno plano horizontal, conforme a figura.
Se o ponto A está a 15 m da base B da torre e o ponto C está
a 20 m de altura, o comprimento do cabo AC é:
C
25m
20m
A
15m
B
(ENEM 2006)Na figura abaixo, que representa o projeto de uma escada
com 5 degraus de mesma altura, o comprimento total do corrimão é
igual a:
A) 1,8 m.
B) 1,9 m.
C) 2,0 m.
D) 2,1 m.
E) 2,2 m.
.
2²
= 1²
+ X²
4
= 4
+ X²
4
-1
= X²
3
= X²
X=√
X=
2
É aproximadamente:
1, 4142135623 7309504880 1688724209 6980785696 7187537694 8073176679
7379907324 7846210703 8850387534 3276415727 3501384623 0912297024
9248360558 5073721264 4121497099 9358314132 2266592750 5592755799
9505011527 8206057147 0109559971 6059702745 3459686201 4728517418
6408891986 0955232923 0484308714 3214508397 6260362799 5251407989
6872533965 4633180882 9640620615 2583523950 5474575028 7759961729
8355752203 3753185701 1354374603 4084988471 6038689997 0699004815
0305440277 9031645424 7823068492 9369186215 8057846311 1596668713
0130156185 6898723723 5288509264 8612494977 1542183342 0428568606
0146824720 7714358548 7415565706 9677653720 2264854470 1585880162
0758474922 6572260020 8558446652 1458398893 9443709265 9180031138
8246468157 0826301005 9485870400 3186480342 1948972782 9064104507
2636881313 7398552561 1732204024 5091227700 2269411275 7362728049
5738108967 5040183698 6836845072 5799364729 0607629969 4138047565
4823728997 1803268024 7442062926 9124859052 1810044598 4215059112
0249441341 7285314781 0580360337 1077309182 8693147101 7111168391
6581726889
4197587165
8215212822
9518488472
08969
3
É aproximadamente:
1.7320508075688772935274463415058723669428052538103806280558069794
519330169088000370811461867572485756756261414154067030299699450949
989524788116555120943736485280932319023055820679748201010846749232
650153123432669033228866506722546689218379712270471316603678615880
190499865373798593894676503475065760507566183481296061009476021871
903250831458295239598329977898245082887144638329173472241639845878
553976679580638183536661108431737808943783161020883055249016700235
207111442886959909563657970871684980728994932964842830207864086039
887386975375823173178313959929830078387028770539133695633121037072
640192491067682311992883756411414220167427521023729942708310598984
594759876642888977961478379583902288548529035760338528080643819723
446610596897228728652641538226646984200211954841552784411812865345
070351916500166892944154808460712771439997629268346295774383618951
101271486387469765459824517885509753790138806649619119622229571105
552429237231921977382625616314688420328537166829386496119170497388
363954959381457576718533736331259108996554246248347871976052359977
691923235702203053028403859154149710724295592067062025095201759631
858727663599752836634310801506658537106473285386259222605822205104
036802702975047987280794616581004170526819400190957334621759438936
702493204226910343698124637201111852610842689102997203112021
8.(UFRGS 2003) Na figura abaixo, os três círculos têm o
mesmo raio r, as retas são paralelas, os círculos são
tangentes entre si e cada um deles é tangente a uma das
duas retas.
Dentre as alternativas abaixo, a melhor
aproximação para a distância entre as
retas é
a) 3r
b) 3,25r
c) 3,5r
d) 3,75r
e) 4r
Teorema de “Pita”:
2r
r
(2r)²=
+x²
(2r) =r²+
4r²=
+x²
4r =r²+
4r²=x²
4r -r²=
3r²=
3r =x²
x=r 3
Calcule a soma dos catetos do triângulo retângulo da figura,
sabendo que AB = 10 e BC = 6.
hipotenusa
x
Um ciclista partindo de ponto A, percorre 15km para norte; a seguir,
fazendo um ângulo de 90°, percorre 20km para leste, chegando ao
ponto B. Qual é a distância, em linha reta, do ponto B ao ponto A?
(UFRGS 2005) Considere os triângulos I, II e III caracterizados abaixo
através das medidas de seus lados.
- triângulo I: 9, 12 e 15.
- triângulo II: 5, 12 e 13.
- triângulo III: 5, 7 e 9.
Quais são triângulos retângulos com as medidas dos lados em progressão
aritmética?
a) Apenas o triângulo I.
b) Apenas o triângulo II.
c) Apenas o triângulo III.
d) Apenas os triângulos I e III.
e) Apenas os triângulos II e III.
hipotenusa²=cateto²+outro cateto²
Hipotenusa
Cateto
a
b
Cateto c
a²=b²+c²
(UFRGS 2005) Considere os triângulos I, II e III caracterizados abaixo
através das medidas de seus lados.
- triângulo I: 9, 12 e 15. PA de razão 3
- triângulo II: 5, 12 e 13.
PA de razão 2
- triângulo III: 5, 7 e 9.
Quais são triângulos retângulos com as medidas dos lados em progressão
aritmética?
a) Apenas o triângulo I.
b) Apenas o triângulo II.
c) Apenas o triângulo III.
d) Apenas os triângulos I e III.
e) Apenas os triângulos II e III.
9
Ok!
12
7
5
Deu merda!
Qual é a área do quadrado azul?
Qual é a distância da linha do horizonte?
Uma pessoa de 1, 80m.
Utilizando o Teorema de
Raio da Terra suposto como 6 371 km. *
Pitágoras e uma calculadora:
6371km+ 1,8m
6371,0018²= 6371²+x²
6371,0018²- 6371² = x²
x²22,53960324 km
x 2,53960324 km
x4,7891 km
x4,79 km
(*)Devido ao fato de que a Terra não é
uma esfera perfeita, não há um único valor
que sirva como seu raio natural. Ao invés
disso, sendo quase esférica, vários valores,
desde o raio polar (de 6 357 km) ao raio
equatorial (6 378 km) são utilizados, de
acordo com a necessidade, e modelos da
Terra assumindo esta como uma esfera
geram um raio médio de 6 371 km
Com o método anterior
podemos criar uma
planilha de calcula a
distância em função da
altura do observador.
(UFRGS – 2012) Observe os discos de raios 2 e 4, tangentes entre si e às
semirretas s e t, representados na figura abaixo.
A distância entre os pontos P e Q é:
a)
b)
c)
d)
e)
9.
10.
11.
12.
13.
t
P
Q
s
ÂNGULOS DOS LADOS PERPENDICULARES
α
α + β = 180°
β
(UFRGS – 2012) Observe os discos de raios 2 e 4, tangentes entre si e às
semirretas s e t, representados na figura abaixo.
A distância entre os pontos P e Q é:
a)
b)
c)
d)
e)
9.
10.
11.
12.
13.
t
P
Q
s
(UFRGS – 2012) Um disco de raio 1 gira ao longo de uma reta
coordenada na direção positiva, como representado na figura abaixo
Considerando-se que o ponto P está inicialmente na origem, à
coordenada de P, após 10 voltas completas, estará entre:
a)
b)
c)
d)
e)
60 e 62.
62 e 64.
64 e 66.
66 e 68.
68 e 70.
(UFRGS 2009). Na figura abaixo, é feito um corte vertical
conforme indicado pela linha pontilhada, obtendo-se , assim,
duas partes. Justapondo-se as partes obtidas, é possível
construir as figuras da opção
.
BARICENTRO:
É o ponto de cruzamento das medianas de um triângulo.
MEDIANA:
Segmento que vai de um vértice até o ponto médio do lado oposto.
A
M, N e P
N
P
BARICENTRO
Pontos Médios
G
B
C
M
AM, BN e CP
AG
GM
=
BG
GN
=
CG
GP
=
2
1
Medianas
ORTOCENTRO:
É o ponto de cruzamento das alturas de um triângulo.
ALTURA:
Segmento que vai de um vértice até o lado oposto, formando um
ângulo de 90º com este.
A
AH, BQ e CW
Q
W
ORTOCENTRO
Alturas
O
B
H
C
IMPORTANTE:
- Num triângulo retângulo, o ortocentro é o vértice reto.
- Num triângulo obtusângulo, o ortocentro é externo ao triângulo.
CIRCUNCENTRO:
É o ponto de cruzamento das mediatrizes de um triângulo.
MEDIATRIZ:
Reta perpendicular a um segmento passando pelo seu ponto médio.
A
Pontos Médios
M, N e P
R = distância do circuncentro aos
R
vértices do triângulo
Q
P
CIRCUNCENTRO
R
B
R
M
IMPORTANTE:
C
R = raio da
circunferência
circunscrita ao triângulo
O circuncentro é:
- o ponto eqüidistante dos vértices do triângulo.
- o centro da circunferência circunscrita ao triângulo.