1.- Indutâncias próprias e mutuas em função da corrente Calculo da

1.- Indutâncias próprias e mutuas em função da corrente
Calculo da indutância própria através do vetor de potencial
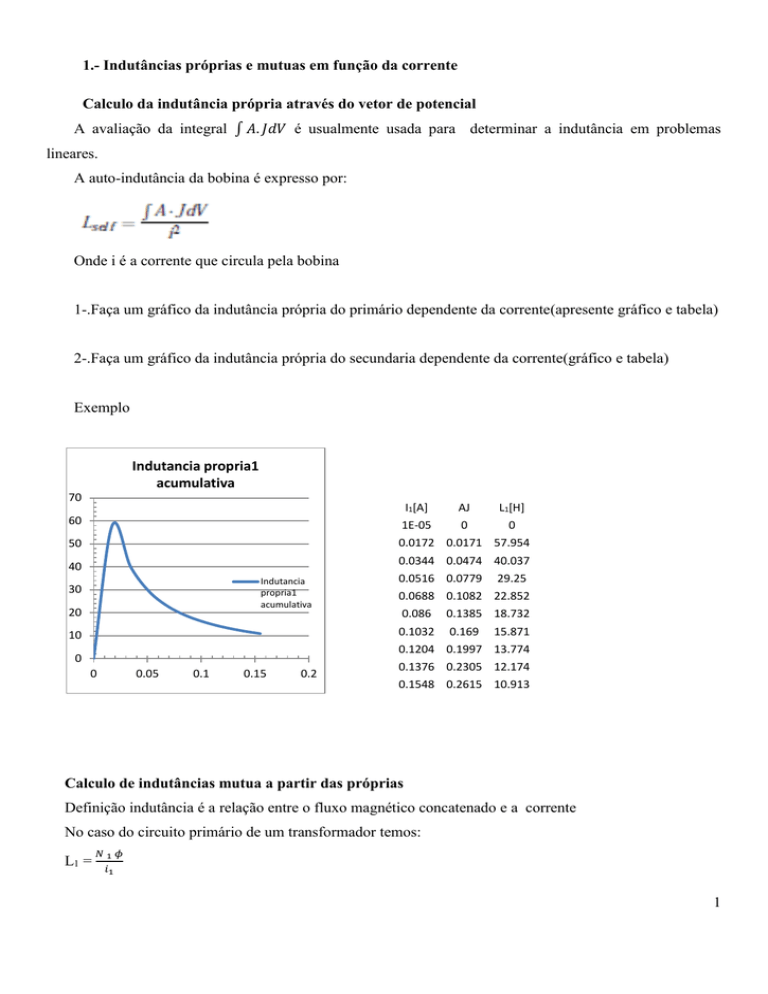
A avaliação da integral ∫ 𝐴. 𝐽𝑑𝑉 é usualmente usada para determinar a indutância em problemas
lineares.
A auto-indutância da bobina é expresso por:
Onde i é a corrente que circula pela bobina
1-.Faça um gráfico da indutância própria do primário dependente da corrente(apresente gráfico e tabela)
2-.Faça um gráfico da indutância própria do secundaria dependente da corrente(gráfico e tabela)
Exemplo
Indutancia propria1
acumulativa
70
I1[A]
AJ
L1[H]
60
1E-05
0
0
50
0.0172 0.0171 57.954
40
0.0344 0.0474 40.037
Indutancia
propria1
acumulativa
30
20
10
0.0516 0.0779
29.25
0.0688 0.1082 22.852
0.086
0.1385 18.732
0.1032
0.169
15.871
0.1204 0.1997 13.774
0
0
0.05
0.1
0.15
0.2
0.1376 0.2305 12.174
0.1548 0.2615 10.913
Calculo de indutâncias mutua a partir das próprias
Definição indutância é a relação entre o fluxo magnético concatenado e a corrente
No caso do circuito primário de um transformador temos:
L1 =
𝑁1𝜙
𝑖1
1
Φ=BA
(1)
B=μH
(2)
H=
𝑛1 𝑖1
(3)
𝑙𝑚
Associando as relações 1,2e3 obtemos uma expressão para o fluxo magnético
Φ=
𝜇𝐴𝑛1 𝑖1
𝑙𝑚1
A expressão para a indutância do primário fica:
L1=
𝜇𝐴𝑛12
[H] ,
𝑙𝑚1
De forma análoga a indutância própria do secundário:
L2=
𝜇𝐴𝑛22
𝑙𝑚2
[H] com lm1=lm2 percurso médio do fluxo
Indutâncias mutuas
Da lei de Faraday
𝑑𝜙
e1= n1 𝑑𝑡
e1= n1
como Φ =
,
𝜇𝐴𝑛1
𝑑𝑖1
𝑙𝑚1
𝑑𝑡
𝜇𝐴𝑛1 𝑖1
𝑙𝑚1
a expressão pode ser rescrita
De forma análoga:
𝑑𝜙
e2= n2 𝑑𝑡 = n2
𝜇𝐴𝑛1
𝑑𝑖2
𝑙𝑚1
𝑑𝑡
Definindo indutância mutua como M21 = n1n2
𝜇𝐴
𝑙𝑚1
[H]
𝑑𝑖1
e2= M21
𝑑𝑡
De forma análoga
e1=M12
𝑑𝑖2
𝑑𝑡
Assim
M21= M12= M = n1n2
𝜇𝐴
𝑙𝑚1
Como
L1=
𝜇𝐴𝑛12
𝑙𝑚1
[H] , L2=
𝜇𝐴𝑛22
𝑙𝑚2
[H] e M21= M12= M = n1n2
𝜇𝐴
𝑙𝑚
E possível relacionar a indutância mutua com as próprias através de:
𝐿
𝐿
.𝑛12 = 𝑛22 =
1
2
𝑀
𝑛1 𝑛2
2
𝑛
A relação de transformação definida como a=𝑛1
2
𝐿
.𝑛12 = 𝑛
𝑀
1 𝑛2
1
/𝑛12 => L1=M*a => M=
𝑳𝟏
𝒂
De forma análoga:
L2 =
𝑀
𝑎
= > M=aL2
O anterior estabelece que a indutância mutua se relaciona em forma proporcional com a indutância
própria tanto primaria como secundaria
3.- Faça o gráfico da indutância mutua dependente da corrente primaria
Obtenção do modelo do núcleo
Indutancia mutua
8
6
4
M
2
0
0
0.05
0.1
0.15
0.2
I1[A]
AJ
L1[H]
M[H]
0.00001
0
0
0.0172
0.01714
57.9535
6.319904
0.0344
0.04738
40.0366
4.366043
0.0516
0.07788
29.2505
3.189799
0.0688
0.10817
22.852
2.492035
0.086
0.13854
18.7324
2.04279
0.1032
0.16903
15.8707
1.730717
0.1204
0.19966
13.7736
1.502025
0.1376
0.23051
12.1744
1.327633
0.1548
0.26151
10.9131
1.19009
0
2.- Modelar o núcleo do transformador
O FEM utiliza um modelo serie para o núcleo , para utilizar o paralelo popularmente utilizado se
deve realizar umas adequações matemáticas no exemplo aparece a metodologia para esta transformação.
Resultados obtidos na simulação para o transformador em vazio , isto I1 = 10% da nominal e I2 = 0
Exemplo do ensaio em vazio
Primário vazio Irms= 12.2mA Ipk=12.2 *√2=0.0172
a=relação transformação =9.17
3
Primario
Apparent Power = 2.22307 VA
Total current = 0.0172 Amps
Secundario
Voltage Drop = 143.398+I*215.075 Volts
Total current = 0 Amps
Flux Linkage = 0.570505-I*0.379756 Webers
Voltage Drop = 15.618+I*23.4595 Volts
Flux/Current = 33.1689-I*22.0788 Henries
Flux Linkage = 0.0622282-I*0.0414279 Webers
Voltage/Current = 8337.1+I*12504.4 Ohms
Real Power = 0 Watts
Real Power = 1.23322 Watts
Reactive Power = 0 VAr
Reactive Power = 1.84965 VAr
Apparent Power = 0 VA
Modelamento do núcleo
Modelo através do FEM (serie)
Voltage/Current = 8337.1+I*12504.4 Ohms
Voltage Drop = 143.398+I*215.075 Volts = 258V
R1
8337
V1
VOFF = 0
VAMPL = 258.5V
FREQ = 60Hz
2
L1
33.17H
1
Obs: FEMM utiliza um modelo serie para o transformador onde R1 representa as perdas do ferro de do
cobre
Mudando de modelo serie para um paralelo equivalente
Considerando os modelos como caixa preta alimentados com a mesma tensão, mesma corrente e mesmo
triangulo de potencias
2
L2
47.914H
V2
VOFF = 0
VAMPL = 258.5V
FREQ = 60Hz
R2
27.092k
1
Potencia ativa
Potencia reativa
P =
Q=
𝑣𝑝2
𝑅𝑝
𝑣𝑝2
𝑋𝐿𝑝
[
=>
Rp =
258.5 2
]
√2
1.23322
[
=>
XLp =
258.5 2
]
√2
1.84965
= 27.092K
= 18.063K => Lp = 47.914H
4
3.- Modelar as perdas por efeito Joule nas bobinas primarias e secundarias
Calculo das resistências primaria e secundarias do bobinado na condição ideal
Através da simulação se obtém as perdas no cobre , na bobina primaria e secundaria, neste exemplo as
correntes primaria de I1=0.1725[A] e secundaria de I2=1.58[A], obtemos atraves da simulação:
Perdida resistiva primaria
𝑃
P1 = 0.201979 Watts => r1=2 𝑖 21 = 6.78Ω
1
𝑃2
Perdida resistiva secundaria P2=0.459849 Watts => r2=2 𝑖 2 = 0.184Ω
2
Perdas no secundário 0.459849 Watts,
corrente=1.58A
Perdas no Primário 0.201979 Watts,
corrente=0.1725A
4.- Modelar o fator de acoplamento magnético
Lembrando das relações obtidas:
A indutância mutua se relaciona com a indutância primaria própria por: M=
𝐿1
𝑎
Isto é : L1 = aM , de modo similar para indutância própria secundaria L2=M/a
Definindo o fator de acoplamento K=
𝑀
√𝐿1 𝐿2
, assim k=1
Neste caso consideraremos a corrente ideal no transformador (sem perdas no núcleo)
Exemplo:
5
Primario
Secundario
Total current = 0.1725 Amps
Total current = 1.58 Amps
Voltage Drop = 12.0552+I*580.418 Volts
Voltage Drop = 1.64146+I*63.3023 Volts
Flux Linkage = 1.53961-I*0.0257655 Webers
Flux Linkage = 0.167915-I*0.00281007 Webers
Flux/Current = 8.92525-I*0.149365 Henries
Flux/Current = 0.106275-I*0.00177852 Henries
Voltage/Current = 69.885+I*3364.74 Ohms
Voltage/Current = 1.0389+I*40.0648 Ohms
Real Power = 1.03976 Watts
Real Power = 1.29675 Watts
Reactive Power = 50.061 VAr
Reactive Power = 50.0088 VAr
Apparent Power = 50.0718 VA
Apparent Power = 50.0257 VA
Calculo da indutância mutua através de fluxo concatenado
M21=
K=
0.167915
= 0.973 ≈ 𝑴𝟏𝟐 =
0.1725
𝟎.𝟗𝟕𝟒
1.5396
1.58
= 0.974
𝟎.𝟗𝟕𝟒
= 𝟎.𝟗𝟕𝟑𝟗 ≈ 1
√8.925∗ 0.106275
5.- Calculo de indutâncias mutuas por energia em condições de polaridade aditiva e subtrativa (
Bucking test)
Energia na curva BH ( características do material)
W=∫ 𝐻𝑑𝑏
𝐵
1
W = ∫ 𝜇 db = 2𝜇B2
Lembrando que :
B=μH
Hlm=Ni
𝜇𝑛1 𝑖1
Assim B =
W=
𝑙𝑚
𝜇 2 𝑛12
1
[
2𝜇
2
𝑙𝑚
] 𝑖12
W*[lm*A]
W*V =
=
𝐿1 ∗𝑖12
/ multiplicando a igualdade por : lmA
1 𝜇𝑛12
[ ]𝑖 2 *A como
2 𝑙𝑚 1
L1=
𝜇𝐴𝑛12
𝑙𝑚1
e lm1=lm2=lm
, Para obter a energia é necessário calcular a área A da curva BH e multiplicar pelo
2
volume encerrado no percurso lm
Energia magnética acumulada no transformador
W=
𝐿1 ∗𝑖12
Como
2
𝐿2 ∗𝑖22
+
2
M=
-M
𝐿1
𝑎
𝑖1 𝑖 2
2
;
= L2a
6
i2=a*i1
L2
=
𝐿1
𝑎2
Expressão de energia em termos L1
W=
𝐿1 ∗𝑖12
2
𝐿1 ∗(𝑎𝑖1 )2
+
Isto é W =
2𝑎2
𝐿1 ∗𝑖12
2
=
𝐿1 𝑖1 (a∗i1 )
-
𝑎
𝐿2 ∗𝑖22
2
=M
2
𝑖1 𝑖2
2
Energia acumulado no indutor na condição acumulativa
Wa =
𝐿1 ∗𝑖12
2
+
𝐿2 ∗𝑖22
2
-M
𝑖1 𝑖2
2
Energia no indutor na condição diferencial
Wd =
𝐿1 ∗𝑖12
2
𝐿2 ∗𝑖22
+
2
+M
𝑖1 𝑖2
2
Assim:
(Wa-Wd )= M𝑖1 𝑖2 (considerando o modulo)
Esta expressão esta em valores de corrente efetivas, o FEMM utiliza valores de corrente de pico, desta forma
a expressão em termos da corrente de pico fica:
M=
𝟐(𝐖𝐚−𝐖𝐝)
𝒊𝟏 𝒊𝟐
Exemplo:
Transformador na condição aditiva (ideal)
Primário
Secundário
Total current = 0.1725 Amps
Total current = 1.58 Amps
Voltage Drop = 12.0552+I*580.418 Volts
Voltage Drop = 1.64146+I*63.3023 Volts
Flux Linkage = 1.53961-I*0.0257655 Webers
Flux Linkage = 0.167915-I*0.00281007 Webers
Flux/Current = 8.92525-I*0.149365 Henries
Flux/Current = 0.106275-I*0.00177852 Henries
Voltage/Current = 69.885+I*3364.74 Ohms
Voltage/Current = 1.0389+I*40.0648 Ohms
Real Power = 1.03976 Watts
Real Power = 1.29675 Watts
Reactive Power = 50.061 VAr
Reactive Power = 50.0088 VAr
Apparent Power = 50.0718 VA
Apparent Power = 50.0257 VA
Calculo das indutâncias mutuas através de fluxo concatenado
7
<None>
0.167915
M21= 0.1725 = 0.9734 [H]
𝑴𝟏𝟐 =
1.53961
1.58
= 0.9744[H]
Calculo das indutâncias mutuas através da energia
Energia na condição acumulativa Wa=0.132272
Joules
M-19
Air
28 AWG
[primario+:1100]
M-19
22 AWG
[secundario+:120]
28 AWG
[primario+:-1100]
22 AWG
[secundario+:-120]
Energia na condição diferencial
Wd= 8.20513e-005 Joules
Para o efeito da corrente diferencial deve-se inverter a polaridade da corrente nas bobinas
M=
𝟐(𝐖𝐚−𝐖𝐝)
𝒊𝟏 𝒊𝟐
=
𝟐(0.132272 −8.20513e−005)
𝟎.𝟏𝟕𝟐𝟓∗𝟏.𝟓𝟖
= 0.97062[H]
l1 = L1 - Ma = 8.92525 - 0.97062*9.17 = 24.6134mH
l2= L2 - M/a = 0.106275 – 0.97062/9.17 = 0.42706mH
Da relação l1= a l2 => l1 = (9.17)2*0.42706mH = 35.9mH
Parte experimental
8
Montar o circuito
Obter os parâmetros do transformador através do ensaio de circuito aberto e em curto circuito do transformador projetado
R1
100k
TX1
V1
VOFF = 0
VAMPL = 311V
FREQ = 60Hz
R4
1k
V
R2
1k
R3
10R
V
0
0
Apresente no relatorio
1.-As formas de onda da tensão e corrente
2.-Angulo de desfasamento
3.-Medir a corrente true rms
4- Apresente um modelo com todos os parâmetros do transformador obtidos no ensaio
5.- Compare o modelo experimental e o teórico ( simulado)
6.- Com os parâmetros do ensaio experimental obtenha o rendimento
8.- Obtenha a regulação do transformador para condições de carga 25%, 50% 75% 100% e 125%
9.- Forma de onda da corrente de Inruhs
10.- O Que é a corrente de inrush e em que casos é importante sua grandeza(pesquiza)
9
Anexos
Teorema da máxima transferência de potencia
A corrente no circuito pode ser calculada como:
A potencia na carga pode ser escrita como:
A potencia na fonte
A potencia maxima na carga se obtem derivando a equação em função do resistor de carga e igualando a
Zero ( condição de pontos de maximos e minimos)
Isto é no caso do transformador , em seu projeto sempre consideraremos que a impedância vista do primário
, deve ser igual à impedância secundaria refletida Z1 = a2Z2
10
Programa Lua
Este programa gera diferentes corrente usadas na simulação (gráficos de indutância)
print("Indutancia")
for x=0.00001,5,1 do
i1= 0.0172*x
i2= 9.17*i1
mi_modifycircprop("primario+",1,i1)
mi_modifycircprop("secundario+",1,i2)
mi_analyze(0)
mi_selectgroup(2)
mi_loadsolution() --Carrega Pós processador
mi_analyze(0)
mi_selectgroup(3)
mi_loadsolution() --Carrega Pós processador
mo_groupselectblock(2)
k= mo_blockintegral(4)
mo_groupselectblock(3)
M= mo_blockintegral(4)
print(format(" %.4f %.8f %.4f %.8f " ,i1, k ,i2,M ))
mo_close()
end
11