Movimento Rotacional

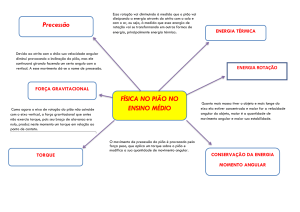
Movimento
Rotacional
Mecânica dos Sólidos
Prof. MSc. Rafael Augusto R de Paula
Momento de Inércia de um Sistema de Partículas
Momento de Inércia para um Corpo Contínuo
ENERGIA CINÉTICA ROTACIONAL
2
Momento de Inércia de um Sistema
de Partículas
1
𝐾=
2
𝒎𝒓𝟐𝒊 𝜔2
𝒊
A grandeza ente é chamada
momento de inércia I do
corpo rígido:
𝑚𝑟𝑖2
𝐼=
𝑖
Fig. 1 - Um corpo rígido girando ao redor do eixo z com
velocidade angular 𝜔. A energia cinética da partícula de
1
massa 𝑚𝑖 é 𝑚𝑖 𝑣𝑖2 . A energia cinética do corpo rígido é
2
chamada sua energia cinética rotacional.
3
Energia Cinética Rotacional e
Momento de Inércia
• Portanto, podemos expressar a energia cinética do corpo
rígido como:
1 2
𝐾 = 𝐼𝜔
2
• Pela definição do momento de Inércia percebe-se que ele tem
dimensões de ML² (𝑘𝑔 ∙ 𝑚2 em unidades de SI).
4
Energia Cinética Rotacional e
Momento de Inércia
• O momento de inércia é o análogo rotacional da massa.
• Momento de inércia é uma medida da resistência à variação
na velocidade angular de um sistema, depende da massa do
corpo rígido e de como a massa está distribuída ao redor do
eixo de rotação.
• O momento de inércia de um corpo em relação a um eixo
depende tanto da massa quanto da distribuição de massa em
relação ao eixo.
5
Um Sistema de Partículas
Girando
• Exemplo 1 - Um corpo em quatro
partículas pontuais, cada uma de
massa 𝑚, ligadas por hastes rígidas
sem massa, formando um retângulo de
lados 2𝑎 e 2𝑏, como mostra a Fig. 2. O
sistema gira com rapidez angular 𝜔 em
torno de um eixo do plano da figura
que passa pelo seu centro, como
mostrado
A) Determine a energia cinética do
corpo, usando as equações:
1
𝐼 = 𝑖 𝑚𝑟𝑖2 e 𝐾 = 𝐼𝜔2
2
B)
Confira seu resultado, separando, a
energia cinética de cada partícula e
somando.
Fig. 2 – Exemplo 1
Resposta:
A) 𝐾 = 2𝑚𝑎2 𝜔2
B) 𝐾 = 2𝑚𝑎2 𝜔2
Os dois cálculo levam ao mesmo
resultado, o que testa a plausibilidade
6
Momento de Inércia para um
Corpo Contínuo
• Para calcular o momento de inércia de corpos contínuos,
considera-se o corpo como constituído de um contínuo de
elementos de massa muito pequenos, Δ𝑚𝑖 . Assim a soma
finita 𝑚𝑖 𝑟𝑖2 torna-se uma integral:
𝑟𝑖2 Δ𝑚𝑖 =
𝐼 = lim
Δ𝑚𝑖 →0
𝑟 2 𝑑𝑚
𝑖
• Pode-se calcular o momento de inércia em termos do
comprimento, área ou volume de seus elementos.
Expressando em forma diferencial o elemento 𝑑𝑚,
respectivamente:
𝜆𝑑ℓ − 𝑚𝑎𝑠𝑠𝑎 𝑝𝑜𝑟 𝑢𝑛𝑖𝑑𝑎𝑑𝑒 𝑑𝑒 𝑐𝑜𝑚𝑝𝑟𝑖𝑚𝑒𝑛𝑡𝑜
𝜎𝑑𝐴 − 𝑚𝑎𝑠𝑠𝑎 𝑝𝑜𝑟 𝑢𝑛𝑖𝑎𝑑𝑒 𝑑𝑒 á𝑟𝑒𝑎
𝑑𝑚 =
𝜌𝑑𝑉 − 𝑚𝑎𝑠𝑠𝑎 𝑝𝑜𝑟 𝑢𝑛𝑖𝑑𝑎𝑑𝑒 𝑑𝑒 𝑣𝑜𝑙𝑢𝑚𝑒
7
Cálculo do Momento de Inércia para
Corpos Contínuos – Exemplos
• Momento de Inércia
de uma barra fina
homogênea de
comprimento 𝐿 e
massa 𝑀 em relação
a um eixo que passa
perpendicularmente
por uma das suas
extremidades.
1
𝐼𝑦 = 𝑀𝐿2
3
8
Cálculo do Momento de Inércia para
Corpos Contínuos – Exemplos
• Aro em relação a um
eixo que passa
perpendicularmente
pelo seu centro:
𝐼 = 𝑀𝑅2
9
Cálculo do Momento de Inércia para
Corpos Contínuos – Exemplos
• Disco homogêneo
em relação a um eixo
que passa
perpendicularmente
pelo seu centro
1
𝐼 = MR2
2
10
Cálculo do Momento de Inércia para
Corpos Contínuos – Exemplos
• Aro em relação a um
eixo que passa
perpendicularmente
pelo seu centro:
1
𝐼 = 𝑀𝑅2
2
11
Momentos de Inércia de Corpos
Homogêneos de Várias Formas
12
O Teorema dos Eixos Paralelos
𝐼 = 𝐼𝑐𝑚 + 𝑀ℎ2
13
Um corpo girando em torno de um eixo paralelo a um eixo que passa pelo
seu centro de massa, sendo h a distância entre os dois eixos.
Aplicando o Teorema dos Eixos
Paralelos
Resposta:
1
𝐼=
𝑀𝐿2
12
• Uma barra fina e
homogênea, de massa 𝑀
e comprimento 𝐿 sobre o
eixo possui uma de suas
extremidades na origem.
• Calcule o momento de
inércia em relação a 𝑦’,
que é paralelo ao eixo y
e passa pelo centro da
barra:
a) Usando o teorema dos
eixos paralelos.
b) Por integração direta.
15
Grandezas Angulares e Vetores
Segunda Lei de Newton para a Rotação
Torque e Quantidade de Movimento Angular
A NATUREZA VETORIAL DA ROTAÇÃO
16
Grandezas Angulares e Vetores
AS GRANDEZAS ANGULARES SÃO VETORES?
• A questão que se levanta é a seguinte: “No caso mais geral,
podemos expressar o deslocamento, a velocidade e a
aceleração angular de um corpo rígido em rotação através de
vetores?”
• A resposta é um “sim” cauteloso.
17
Sentido do Vetor Velocidade
Angular
18
Grandezas Angulares e Vetores
• A representação de grandezas angulares por meio de vetores
não é tão fácil de compreender como a representação de
grandezas lineares.
• Instintivamente, esperamos que algo se mova na direção do
vetor. Não é o que acontece.
• No mundo das rotações puras, um vetor define um eixo de
rotação, não uma direção de movimento.
• A aceleração angular α obedece as mesmas regras.
19
Deslocamentos Angulares
• Para ser representada como
um vetor, uma grandeza
também precisa obedecer às
regras da soma vetorial, uma
das quais diz que, quando
somados dois vetores, a
ordem na qual os vetores são
somados é irrelevante. O
deslocamento angular não
passa neste teste (Veja a
figura).
• Embora os dois deslocamentos
angulares sejam iguais nos
dois casos, a ordem é
diferente e o livro termina com
orientações diferentes.
20
Segunda Lei de Newton para a Rotação
Calculando Torques
Torque e o Produto Vetorial
Torque e Momento Angular
TORQUE E QUANTIDADE DE
MOVIMENTO ANGULAR
21
Segunda Lei de Newton para a Rotação
II) Se as mesmas forças são aplicadas nos
I) Um disco é posto para girar pelas
forças 𝐹1 e 𝐹2 exercidas tangencialmente mesmos pontos, mas em uma direção
radial o disco não começará a girar.
nas bordas.
III) Se as mesmas forças são aplicadas
tangencialmente, mas em pontos mais
próximos ao centro do disco, o disco não
ganha rapidez angular tão rapidamente.
Percebe-se que os sentidos destas forças e
seus pontos de aplicação são importantes.
22
Segunda Lei de Newton para a Rotação
Torque em Relação a um Eixo
A figura mostra uma partícula de
massa m presa por uma das
extremidades, a partícula está
limitada a se mover em um círculo de
raio r. Uma única força 𝐹 é aplicada.
Pela segunda lei de Newton:
𝐹𝑡 = 𝑚𝑎𝑡
Substituindo 𝑎𝑡 por 𝑟𝛼 e
multiplicando os dois lados por 𝑟:
𝑟𝐹𝑡 = 𝑚𝑟 2 𝛼
O produto 𝑟𝐹𝑡 é o TORQUE 𝜏 em relação ao eixo de rotação associado
à força. Isto é:
𝜏 = 𝑟𝐹𝑡
23
Segunda Lei de Newton para a Rotação
• Substituindo 𝑟𝐹𝑡 por 𝜏:
𝜏 = 𝑚𝑟 2 𝛼
• Um corpo rígido que gira em torno de um eixo fixo é
simplesmente uma coleção de partículas restritas a um
movimento circular com as mesmas 𝜔 e 𝛼.
• Agora somamos os torques sobre todas as partículas do corpo
rígido e teremos o torque resultante sobre o corpo rígido:
𝑚𝑖 𝑟𝑖2 𝛼𝑖 =
𝜏𝑖 =
𝑖
𝑖
𝑚𝑖 𝑟𝑖2 𝛼
𝑖
24
Segunda Lei de Newton para a Rotação
• Portanto:
𝜏 = 𝐼𝛼
SEGUNDA LEI DE NEWTON PARA A ROTAÇÃO
• O torque resultante agindo sobre o corpo rígido é
proporcional a sua aceleração angular.
• A constante de proporcionalidade é o momento de inércia
• Esta equação é o análogo rotacional da segunda lei de Newton
para o movimento de translação: 𝐹 = 𝑚𝑎.
25
Enigma Rápido 10.9
• (SERWAY, 2007) Se você desliga o esmeril da sua oficina ao
mesmo tempo em que sua furadeira elétrica, o esmeril leva
muito mais tempo para parar de girar. Por que?
Resposta: Tanto o esmeril quanto a furadeira tornam-se mais lentos
devido ao torque de atrito nas rolimãs do motor. Vamos considerar
que esse torque devido ao atrito nas rolimãs seja aproximadamente
o mesmo nas duas ferramentas . O esmeril é um disco grande com
uma massa elevada, e a parte que gira em uma furadeira elétrica é
um cilindro pequeno de massa relativamente pequena. Assim, o
esmeril tem um momento de inércia maior que a broca da
furadeira, tanto devido à sua massa maior quanto devido à sua
forma. De acordo com a equação 𝜏 = 𝐼𝛼, um momento de inércia
maior resulta em uma aceleração angular menor para o mesmo
torque e um tempo correspondente maior para atingir o repouso.
26
Calculando Torques
• A força 𝐹 produz um
torque 𝜏 = 𝑟𝐹𝑡 ;
• Da figura podemos
ver que:
𝐹𝑡 = 𝐹 sin 𝜙
• Assim, podemos
escrever o torque
como:
𝜏 = (𝐹 sin 𝜙)𝑟
27
𝜙 é o ângulo entre as direções
radial e da força.
Calculando Torques
• A linha de ação de uma
força é a linha paralela à
força que passa pelo seu
ponto de aplicação,
podemos ver que:
𝑟 sin 𝜙 = ℓ
• Consequentemente:
𝜏 = 𝐹ℓ
EXPRESSÕES EQUIVALENTES
PARA O TORQUE:
𝜏 = 𝐹𝑡 𝑟 = 𝐹 sin 𝜙𝑟 = 𝐹ℓ
Linha de
Ação
ℓ é o braço de alavanca ,
distância perpendicular
entre A e a linha de ação.
28
Exemplo 10.6 - O Torque
Resultante sobre um Cilindro
(SERWAY, 2007) Um cilindro maciço tem a forma mostrada na figura com
um núcleo projetando-se para fora da parte cilíndrica maior. O cilindro é
livre par girar ao redor do eixo central mostrado no diagrama. Uma corda
enrolada ao redor da parte cilíndrica maior de raio 𝑅1 , exerce uma força
𝑇1 para a direita sobre o cilindro. Uma corda enrolada ao redor do
núcleo, de raio 𝑅2 exerce uma força 𝑇2 para baixo sobre o cilindro.
(a) Qual é o torque resultante agindo
sobre o cilindro ao redor do eixo de
rotação?
(b) Suponha que 𝑇1 = 5,0 𝑁, 𝑅1 =
1,0 𝑚, 𝑇2 = 6,0 𝑁, e 𝑅2 =
0,50 𝑚. Qual é o torque resultante
ao redor do eixo de rotação e em
qual sentido o cilindro vai começar a
girar se parte do repouso?
29
Segunda Lei de Newton
Exercício 1) O aparelho da figura é chamado de
máquina de Atwood e é usado para medir a
aceleração de queda livre 𝑔 medindo-se a
aceleração dos dois blocos ligados pelo fio que
passa pela polia. Suponha uma polia sem
massa e sem atrito e um fio sem massa.
(a) desenhe o diagrama de corpo livre de cada
bloco.
(b) Use os diagramas de corpo livre e as leis de
Newton para mostrar que a magnitude da
aceleração de cada bloco e que a tensão no
𝑚1 −𝑚2
2𝑚1 𝑚2
fio são 𝑎 =
𝑔e𝑇 =
𝑔
(𝑚1 +𝑚2 )
(𝑚1 +𝑚2 )
(c) Estas expressões fornecem resultados
plausíveis se 𝑚1 = 𝑚2 ? Explique
30
Dois Blocos e uma Polia
Exercício 2) O sistema
mostrado na figura é
largado do repouso. A
massa da polia não é
desprezível, mas o
atrito no suporte é
desprezível. O fio não
deslize na polia. Dado
que 𝑚1 > 𝑚2 , o que
se pode dizer das
tensões 𝑇1 e 𝑇2 ?
31
Dois Blocos e uma Polia
• Exercício 2) Resposta:
Após a largada, 𝑚1 vai acelerar para baixo, 𝑚2 vai acelerar para
cima e a polia vai acelerar angularmente no sentido anti-horário.
Como 𝑚1 acelera para baixo, a força resultante sobre esse bloco
deve ser para baixo:
𝑚1 𝑔 < 𝑇1
Como 𝑚2 acelera para cima, a força resultante sobre este bloco
deve ser para cima:
𝑇2 > 𝑚2 𝑔
Como a aceleração angular da polia é anti-horária , o torque
resultante sobre ela deve ser anti-horário. Como os dois braços de
alavanca são iguais, torque maior significa tensão maior:
𝜏1 > 𝜏2 𝑙𝑜𝑔𝑜 𝑇1 > 𝑇2
Combinando os três resultados:
𝑚1 𝑔 > 𝑇1 > 𝑇2 > 𝑚2 𝑔
32
Exemplo 10.10 - Uma Máquina de
Atwood com uma Polia com Massa
(SERWAY, 2007)
Analisamos uma máquina de Atwood na qual dois corpos com
massas desiguais estão dependuradas por um fio que passa por
uma polia leve sem atrito. Imagine que a polia, que é modelada
como um disco, tenha massa M e raio R, e que a superfície da
polia tenha atrito, de forma que o fio não deslize sobre a polia.
Vamos supor que o torque de atrito atuando na rolimã da polia
seja desprezível. Calcule o módulo da aceleração dos dois
corpos.
Resposta:
𝑎=
𝑚1 −𝑚2
1
𝑚1 +𝑚2 +2𝑀
𝑔
33
Exercícios
Exercício 3) Para exercitar-se sem
sair do lugar, você montou sua
bicicleta sobre um suporte, de
forma que a roda traseira fico livre
para girar. Enquanto você pedala, a
corrente exerce uma força de 18 𝑁
sobre a catraca traseira, a uma
distância 𝑟 = 7,0 𝑐𝑚 do eixo de
rotação da roda. Considere a roda
como um aro 𝐼 = 𝑀𝑅2 de raio
𝑅 = 35 𝑐𝑚 e massa 𝑀 = 2,4 𝑘𝑔.
Qual é a velocidade angular da
roda 5,0 𝑠 depois?
Resposta: 𝜔 = 21,4 𝑟𝑎𝑑/𝑠
34
Uma Barra Homogênea Pivotada
Exercício 4) Uma barra fina homogênea de comprimento 𝐿
e massa 𝑀 é articulada em uma de suas extremidades. Ela
é largada da posição horizontal. Despreze o atrito e a
resistência do ar. Determine
(a) A aceleração angular da barra, imediatamente após ser
largada;
(b) A magnitude da força 𝐹𝐴 exercida sobre a barra pelo
pivô neste instante
Resposta:
3𝑔
a) 𝛼 =
1
2𝐿
b) 𝐹𝐴 = 4 𝑀𝑔
35
Dois Blocos e uma Polia II
Exercício 5) Dois blocos estão ligados por um fio que
passa por uma polia de raio R e momento de inércia I. O
bloco de massa 𝑚1 desliza sobre uma superfície
horizontal sem atrito; o bloco de massa 𝑚2 está
suspenso pelo fio. Determine a aceleração 𝑎 dos blocos
e as tensões 𝑇1 e 𝑇2 . O fio não desliza na polia.
Resposta:
• 𝑎=
• 𝑇1 =
• 𝑇2 =
𝑚2
𝑚1 +𝑚2 +
𝑚2
𝐼 2
𝑅
𝐼 2
𝑚1 +𝑚2 +
𝑅
𝐼 2
𝑚1 + 𝑅
𝐼 2
𝑚1 +𝑚2 + 𝑅
𝑔
𝑚1 𝑔
𝑚2 𝑔
36
Torque e o Produto Vetorial
• O vetor torque é
definido como igual
ao produto vetorial
de 𝑟 e 𝐹 :
𝜏 =𝑟×𝐹
37
O Produto Vetorial
• O produto vetorial 𝐴 × 𝐵 é um terceiro vetor 𝐶 tendo
um módulo 𝐴𝐵 sin 𝜃.
• O vetor 𝐶 é perpendicular ao plano formado por 𝐴 e 𝐵.
• Sua direção é determinada pela regra da mão direita.
38
Torque e o Produto Vetorial
• Na figura, o vetor
torque tem
magnitude Fr e a
direção do eixo de
rotação como o
sentido mostrado.
39
Produto Vetorial – Vetores
Unitários
Sistema coordenado direito. O produto vetorial feito na ordem das setas
da figura (sentido horário) é positivo (𝑖 × 𝑗 = 𝑘). Na ordem inversa, o
sinal é negativo.
40
Enigma Rápido 10.6
• Tanto o torque quanto o trabalho são produtos de força e
distância. De que forma eles são diferentes?
Torque e trabalho apresentam duas diferenças
importantes. A diferença principal é que o vetor
deslocamento na expressão trabalho é direcionado de
forma paralela à força, mas o vetor posição na
expressão do torque é perpendicular à força. A segunda
diferença depende se há ou não movimento – no caso do
trabalho, é realizado trabalho apenas se a força
consegue causar um deslocamento do ponto de
aplicação da força. Por outro lado, uma força aplicada
em uma distância perpendicular ao eixo de rotação
resulta em um torque, havendo ou não movimento.
41
Exercício
Exercício 6) Uma partícula está localizada no vetor posição
𝑟 = 𝑖 + 3j 𝑚, e a força agindo sobre ela é 𝐹 = 3𝑖 + 2𝑗 𝑁.
Qual é o torque sobre a partícula ao redor de um eixo passando:
(a) Pela origem?
(b) Por um ponto tendo coordenadas (0, 6)m?
(SERWAY, p. 330, vol.1, 2007).
42
Torque e Momento Angular
Momento Angular de um Corpo com Momento de Inércia I
Segunda Lei de Newton para o Movimento de Rotação
Lei da Conservação da Quantidade de Movimento Angular
TORQUE E MOMENTO ANGULAR
43
Torque e Momento Angular
Uma partícula de massa m
se movendo com velocidade
𝑣 na posição 𝑟 em relação a
origem.
Tem quantidade de
movimento linear:
𝑝 = 𝑚𝑣
A quantidade de movimento
angular 𝐿 da partícula em
relação a origem O é definida
como:
𝐿 =𝑟×𝑝
44
Torque e Momento Angular
A figura mostra uma
partícula de massa m, presa a
um disco circular de massa
desprezível, movendo-se em
um círculo no plano xy que
tem o centro na origem, o
disco gira em torno do eixo z,
com rapidez angular 𝜔, deste
modo:
𝐿 × 𝑝 = 𝑟 × 𝑚𝑣
= 𝑟𝑚𝑣 sin 90°𝑘
𝐿 × 𝑝 = 𝑟𝑚𝑣𝑘 = 𝑚𝑟 2 𝜔𝑘
= 𝑚𝑟 2 𝜔
45
Torque e Momento Angular
• Como 𝑚𝑟 2 é o
momento de inércia de
uma única partícula
em relação ao eixo z,
temos
• 𝐿 = 𝑚𝑟 2 𝜔 = 𝐼𝜔
• Neste exemplo, o vetor
quantidade de
movimento angular
tem a mesma
orientação do vetor
velocidade angular.
46
Torque e Momento Angular
• A figura mostra o vetor
quantidade de
movimento angular 𝐿′
da mesma partícula,
mas com 𝐿′ calculado
em relação a um ponto
do eixo 𝑧 que não está
no centro do círculo.
Neste caso, a
quantidade de
movimento angular
não é paralelo ao vetor
velocidade angular 𝜔.
47
Momento Angular de um Corpo
com momento de Inércia I
• Um corpo rígido quando ao redor de um eixo, cada partícula de massa
𝑚𝑖 no corpo rígido descreve uma trajetória circular de raio 𝑟𝑖 , com
velocidade tangencial 𝑣𝑖 . Assim o momento angular total:
𝐿=
𝑚𝑖 𝑣𝑖 𝑟𝑖
𝑖
• Temos que: 𝑣𝑖 = 𝜔𝑟𝑖 .Num corpo rígido todas as partículas se movem
com mesmo 𝜔:
𝑚𝑖 𝑟𝑖2 𝜔
𝐿=
• Reconhecemos que 𝐼 =
𝑖
2
𝑖 𝑚𝑖 𝑟𝑖 ,
assim:
𝐿 = 𝐼𝜔
• É o análogo rotacional de 𝑝 = 𝑚𝑣.
48
Momento Angular
𝐿 = 𝑟 × 𝑝 = 𝑚𝑣𝑟 sin 𝜃
• Se 𝑟 e 𝑝 são paralelos, 𝜃 = 0 𝑜𝑢 180°, sin 𝜃 = 0, então:
𝐿=0
Significa que a partícula está em movimento ao longo de uma
linha que passa pela origem.
• Se 𝑟 e 𝑝 são perpendiculares, sin 𝜃 = 1, então:
𝐿 = 𝑚𝑣𝑟
Significa que 𝐿 é máximo.
• Unidade SI:
𝑚2
𝑘𝑔
𝑠
49
Segunda Lei de Newton para o
Movimento de Rotação
• O torque externo resultante sobre um sistema em relação a
um ponto fixo é igual a taxa de variação da quantidade de
movimento angular do sistema em relação ao mesmo ponto.
𝑑𝐿𝑠𝑖𝑠
𝜏𝑟𝑒𝑠 =
𝑑𝑡
• O momento angular só pode variar no tempo se o um torque
externo resultante age no sistema.
• Este resultado é o análogo rotacional da Segunda Lei de
Newton:
𝑑𝑃
𝐹=
𝑑𝑡
50
Segunda Lei de Newton para o
Movimento de Rotação
• TORQUE É IGUAL À TAXA TEMPORAL DE VARIAÇÃO DO
MOMENTO ANGULAR
𝑑
𝜏= 𝐿
𝑑𝑡
51
Lei da Conservação da Quantidade
de Movimento Angular
• Se o torque externo resultante sobre um sistema em relação a
um ponto é zero, então a quantidade de movimento angular
total do sistema em relação ao mesmo ponto permanece
constante:
𝑑
𝜏𝑒𝑥𝑡 𝑟𝑒𝑠 = 𝐿𝑠𝑖𝑠 = 0;
𝑑𝑡
𝐸𝑛𝑡ã𝑜 𝐿𝑠𝑖𝑠 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒.
52
Lei da Conservação da Quantidade
de Movimento Angular
• Uma patinadora
rodopiando. Como o
torque exercido pelo
gelo é pequeno, a
quantidade de
movimento angular da
patinadora é
aproximadamente
constante. Quando ela
diminui seu momento
de inércia recolhendo
os braços, sua
velocidade angular
aumenta.
53
Exercício 7) Determine a quantidade de movimento
angular, em relação à origem, para as seguintes
situações:
(a) Um carro de 1200 𝑘𝑔 de massa que se move em um círculo
de 20 𝑚 de raio com uma rapidez de 15 𝑚/𝑠. O círculo está
no plano 𝑥𝑦, centrado na origem. Visto de um ponto do eixo
𝑧 positivo, o carro se move no sentido anti-horário (trate o
carro como uma partícula pontual).
(b) O mesmo carro, movendo-se no plano 𝑥𝑦 com velocidade
𝑣 = − 15 𝑚 𝑠 𝑖, ao longo da linha 𝑦 = 𝑦0 = 20 𝑚,
paralela ao eixo x.
(c) Um disco homogêneo no plano 𝑥𝑦, de raio 20 𝑚 e massa
1200 𝑘𝑔, girando a 0,75 𝑟𝑎𝑑/𝑠 em torno de seu eixo, que
também é o eixo 𝑧. Visto de um ponto do eixo 𝑧 positivo, o
disco se move no sentido anti-horário.
54
Figuras para o exercício 7
A)
B)
55
Figuras para o exercício 7
C)
56
Referências
• Allen, TIPLER, P., MOSCA, Gene. Física para Cientistas e
Engenheiros - Vol. 1 – Mecânica ,Oscilações e Ondas,
Termodinâmica, 6ª edição. LTC, 07/2012.
• HALLIDAY, David; RESNICK, Robert; WALKER, Jearl.
Fundamentos de física: mecânica. 9.ed. Rio de Janeiro: LTC,
2012. v.1. 395
• SERWAY, Raymond A; JEWETT JR.,John W. Princípios de
física. São Paulo: Thomson Learning, 2007. v.1. 403 p.
• SERWAY, R. A., & JEWEET, W. J. Physics for Scientists and
Engineers (6ª ed.). Brooks Cole, 2003.
57