PROPOSTA DIDÁTICA 1. Dados de Identificação 1.1 Nome do

MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
PIBID – Programa Institucional de Bolsas de Iniciação à Docência
PROPOSTA DIDÁTICA
1. Dados de Identificação
1.1 Nome do bolsista: Jéssica Marilda Gomes Mendes
1.2 Público alvo: 6º e 7º ano
1.3 Duração:3 períodos de 40 min
1.4 Conteúdo desenvolvido: Números ímpares, números pares, multiplicação e divisão
2. Objetivo(s) da proposta didática
- Mostrar aos alunos que a matemática é interessante e atrativa;
- Desenvolver o conhecimento da matemática dentro de um contexto lúdico.
3. Desenvolvimento da proposta didática
(10 min) - Acomodação dos alunos, apresentação dos bolsistas e realização da chamada.
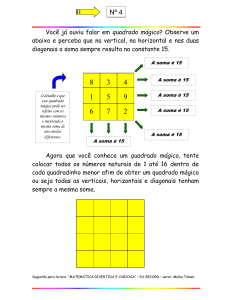
(10 min) – Apresentação dos quadrados mágicos.
Um quadrado mágico é uma tabela quadrada de lado n, onde a soma dos números das
linhas, das colunas e das diagonais é constante, sendo que nenhum destes números se
repete.
Exemplo:
(20 min) - Origem dos quadrados mágicos.
Há diversas versões sobre a origem dos quadrados mágicos, no entanto, pensa-se que
a sua origem tenha vindo da China e da Índia. Os historiadores dizem que os quadrados
mágicos terão surgido há cerca de 3000 anos (na China e da Índia). O nome quadrado
mágico foi dado, pois na época achava-se que este tipo de quadrado tivesse poderes
especiais.
MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
PIBID – Programa Institucional de Bolsas de Iniciação à Docência
Cerca de 2200 a.c., o imperador-engenheiro Yu, o Grande, estaria a observar o rio
Amarelo quando viu uma tartaruga divina, que naquela época era considerado um animal
sagrado, onde em seu casco estava o símbolo que hoje em dia é conhecido pelo nome de lo
shu. Assim, Yu percebeu que as marcas nas costas da tartaruga (que forma o símbolo com
nós) podiam ser transformadas em números de um a nove e que todos eles somavam quinze
em todas as direções, como se fossem algarismos mágicos.
Por esse motivo, os chineses acreditaram durante vários anos que quem possuísse um
quadrado mágico teria sorte e felicidade para toda a vida. Acreditava-se que ele era o símbolo
que reunia os princípios básicos que formavam o universo, onde os números pares
simbolizavam o princípio feminino, Yin, os números ímpares simbolizavam o princípio
masculino, o Yang, e o número 5 representava a Terra e ao seu redor estão distribuídos os
quatro elementos principais, a água 1 e 6, o fogo 2 e 7, a madeira 3 e 8 e os metais 4 e 9.
MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
PIBID – Programa Institucional de Bolsas de Iniciação à Docência
A primeira impressão de um quadrado mágico surgiu em uma gravura intitulada
Melancolia do pintor e gravador alemão do Renascimento Albrecht Dürer, onde neste
quadrado mágico tem quatro numerais horizontais e quatro outros dispostos verticalmente,
sendo as somas iguais a 34.
(20 min) – Como funcionam os quadrados mágicos.
Para montar um quadrado mágico o que devemos calcular em primeiro momento a
constante, número que indica o resultado da soma das linhas e colunas. Este número é
calculado por uma fórmula:
(1º
)
+ ú
=
2
x
nº da ordem
Existem certos modelos de quadrados mágicos que recebem classificação especial
devido a suas singularidades:
Imperfeito é aquele que a soma das linhas e colunas são iguais, mas a das diagonais
não.
12
14
4
6
13
3
5
11
2
8
10
16
7
9
15
1
MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
PIBID – Programa Institucional de Bolsas de Iniciação à Docência
Hipermágico é um quadrado mágico onde trocando duas colunas de lugar, forma-se
um outro quadrado mágico.
2
7
6
9
5
1
4
3
8
(20min ) - Vejamos agora como montar um quadrado mágico 3x3.
Para montar um quadrado mágico 3X3, temos duas maneiras de resolução.
PRIMEIRA RESOLUÇÃO
O quadrado mágico 3x3 é uma tabela quadrada de lado 3, onde a soma dos números
das linhas, a soma dos números das colunas e a soma dos números das diagonais é sempre
um mesmo valor, e os nove números dentro do quadrado não se repetem.
 Calculando a constante de um quadrado mágico 3x3 com os números (1,2,3,4,5,6,7,8,9)
temos que:
(1 + 9) 9 45
=
= 15
2
3
 O número a ser colocado no centro do quadrado deve ser o resultado da divisão da
constante pelo número da ordem.
÷ ú
=
Exemplo:
5
Pois 15 ÷ 3 = 5.
 Se no centro foi colocado um número ímpar, nos cantos deverão ser colocados números
pares.
8
6
5
4
2
MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
PIBID – Programa Institucional de Bolsas de Iniciação à Docência
 E então preenchemos os outros espaços com os números restantes.
8
1
6
3
5
7
4
9
2
SEGUNDA RESOLUÇÃO
Para calcular um quadrado mágico 3x3 temos que colocar sempre o primeiro número
no meio da primeira linha ou última. Distribuir os outros seguindo a sequência colocando
sempre o próximo número na diagonal á direita
8
1
6
3
5
7
4
9
2
(20 min) - Neste momento será pedido para que os alunos se dividam em grupos e, seguindo
os passos dados anteriormente, montem um quadrado mágico 3x3, cada grupo resolverá de
uma forma para que no final se perceba que chegamos em um quadrado mágico.
 Sequência 2,3,4,5,6,7,8,9,10;
 Sequência 3,4,5,6,7,8,9,10,11 e
 Sequência 1,2,3,4,5,6,7,8,9
(20 min) - Para calcular um quadrado mágico 4x4.
 Distribuir os números consecutivos.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 Inverta os números das diagonais e os que tiverem no centro com suas diagonais.
MINISTÉRIO DA EDUCAÇÃO
SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
PIBID – Programa Institucional de Bolsas de Iniciação à Docência
16
2
3
13
5
11
10
8
9
7
6
12
4
14
15
1
Para finalizar os quadrados mágicos 4x4 será distribuído uma tabela 4x4 para
construam
o
quadrado
mágico
da
sequência
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,
distribuindo de forma como foi explicado.
4. Referências Bibliográficas
BARBOSA,R.M.-Aprendendo com padrões mágicos;Coleção Caderno Ensino- Aprendizagem
de Matemática n.1, SBEM, 2000.
CARVALHO,
Jaime.
A
história
dos
quadrados
mágicos.
Disponível
em
<http://www.mat.uc.pt/~mat0717/public_html/Cadeiras/1Semestre/O%20que%20%C3%A9%2
0um%20quadrado%20m%C3%A1gico.pdf>. Acesso em: 12 jun. 2015.
JANUARIO, G. Quadrados mágicos: uma proposta de aprendizado com enfoque
etnomatemático.
Disponível
em:<http://www.diaadiaeducacao.pr.gov.br/diaadia/diaadia/arquivos/File/conteudo/artigos_tes
es/METAMATICA/Artigo_Gilberto_02.pdf >.Acesso em: 10 jun. 2015.
OLEANDRO, Alex.Quadrados mágicos 3X3: um Novo Olhar. Disponível
<file:///D:/RPM%201%20a%2065/pesquisa_mn.htm>.Acesso em: 15 jun. 2015.
em
: