Quadrado mágico

Quadrado mágico
https://wiki.dcc.ufba.br/TecCiencia/QuadradoMagico
Quadrado Mágico é uma tabela quadrada de lado , onde a soma dos números das linhas, das
colunas e das diagonais é constante, sendo que nenhum destes números se repete. Veja os
exemplos:
Fonte:
http://nautilus.fis.uc.pt/mn/quadrado/index.html
Fonte:
http://www.profcardy.com/matematica/magico/3x3.htm
Estas são 2 soluções para os quadrados mágicos 3X3 com as seqüências 28,29,30,31,32,33,34,35 e
36 e 0,1,2,3,4,5,6,7 e 8.
Para estas 2 seqüências de números existem outras soluções? Ou melhor, pergunte aos alunos se
existem outros arranjos possíveis em que todas as colunas, linhas e diagonais apresentem a mesma
soma.
Podemos trabalhar na sala de aula com o quadrado mágico como sugestão para verificar as relações
existentes entre os números e se elas permanecem quando procuramos novas soluções.
Material utilizado: tabuleiro e 9 fichas de cartolina numeradas sequencialmente, sugerimos iniciar
com os números de 1 a 9.
Participantes: é indicado que a sala seja dividida em 5 grupos, para o manuseio.
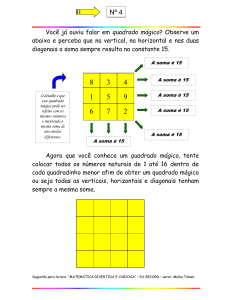
Objetivo: colocar as fichas no tabuleiro de tal forma que a soma das 3 linhas, das 3 colunas e das 2
diagonais seja igual a 15.
Veja algumas dicas para solucionar o quadrado mágico 3x3:
•
•
•
•
O total que se quer obter em todos os sentidos deverá ser dividido por 3. O que resultará no
número a ser colocado no centro do quadrado.
Os números a serem colocados nos cantos deverão ser pares se o centro for ímpar, ou vice e
versa.
O último número a ser colocado deverá ser o centro mais 4.
Essas regras só valem se os números forem múltiplos de 3. Ex: 15, 18, 21, 24, 27, 30 etc.
A base matemática para a resolução do problema, do quadrado mágico 3X3 com a série de
números 1 a 9, é:
A soma S n = 45 para 1 ≤ n ≤ 9 . Isto é, S n = 1+2+3+4+5+6+7+8+9 = 45.
A soma de três parcelas no tabuleiro em qualquer linha, coluna ou diagonal deve ser igual a 45/3 =
15.
Obs: Só é possível montar o quadrado mágico proposto se o número 5 ocupar a casa central do
tabuleiro.
Consideramos as casas do tabuleiro numeradas da seguinte forma :
a1
a2
a3
a4
a5
a6
a7
a8
a9
Temos:
+
a 1+ a5 + a9 = 15
a2 + a5 + a8 = 15
a3 + a5 + a7 = 15
a4 + a5 + a6 = 15
a 1+ a2 + a3+...+a9 + 3a5= 60
45
45+3a5= 60
3a5= 15
a5 =
15
=5
3
Depois que os alunos treinem bastante com o quadrado mágico 3X3, com os números de 1 a 9, tente
estabelecer com eles a relações que sempre permanecem, mesmo que se mude a organização dos
números. Depois peça-lhes que mudem a sequencia e verifiquem o que permanece verdadeiro, isto
pode ser feito aqui http://www.profcardy.com/matematica/magico/3x3.htm (neste site só se pode
usar a seqüência de 0 a 8), podemos pedir-lhes para tentarem com outras seqüências de números e
que eles estabeleçam as regras para encontrar a solução para qualquer seqüência de números.
Os alunos podem comprovar que podemos usar quaisquer seqüências de números para arrumar um
quadrado mágico, eles podem treinar em http://nautilus.fis.uc.pt/mn/quadrado/index.html
E
como
desafio
vc
pode
tentar
resolver
o
que
está
proposto
em
http://nautilus.fis.uc.pt/mn/quadrado10000/quadrado10000.php (aqui cada vez que se atualiza a
página web aparece um novo desafio).
Agora sugira que eles tentem trabalhar com um quadrado mágico 4X4 e verifiquem quais são as
relações que permanecem.
Será que podemos agora encontrar uma regra geral para resolver qualquer quadrado mágico?
Aqui http://www.ziggi.com.br/downloadnow/23460/ se pode fazer o download de um jogo
quadrado mágico (precisa baixar e conferir se vale a pena).
Outra sugestão para trabalhar com o quadrado mágico está em
http://blogs.esecs.ipleiria.pt/eb1mat/files/2007/03/quadrados_magicos.pdf
Esta atividade foi desenvolvida pela
Profa Frieda para o Projeto Educandow e
contou com a colaboração da aluna de
Matemática da UFBA, Jamille Vilas Boas.
Maio/2009