Entropia Energia de Gibbs e Equilíbrio

Entropia
Energia de Gibbs e Equilíbrio
Mestrado integrado em Engenharia Biológica
Disciplina Química II, 2º semestre 2009/10
Professsora Ana Margarida Martins
TRANSFORMAÇÕES ESPONTÂNEAS
Uma reacção diz-se espontânea se ocorre quando se juntam os reagentes em
determinadas condições de pressão, temperatura, pressão, concentração, etc.
Por exemplo,
À temperatura ambiente, o sódio reage
espontanea e irreversivelmente com água,
com libertação de calor
Na + H2O
NaOH + ½ H2
Mas há reacções espontâneas que requerem energia do exterior. Por exemplo,
O NH4NO3 dissolve-se espontaneamente em água, à temperatura ambiente,
absorvendo energia,
NH4NO3(s)
H2O
NH4+(aq) + NO3─(aq)
A adição do sólido ao copo
provoca uma diminuição da
temperatura da solução
Outras reacções podem não ser espontâneas à temperatura ambiente, mas sê-lo
a temparaturas mais elevadas, como, por exemplo, a decomposição de HgO
2HgO(s)
2Hg(l) + O2(g)
DH0 = 90,7 kJ
Outras reacções ainda, embora favoráveis do ponto de vista entálpico, não
ocorrem espontaneamente sem uma fonte de ignição, como a combustão do
metano
CH4(g) + 2O2(g)
CO2(g) + 2H2O(l)
DH0 = ─890,4 kJ
A entalpia não é, por si só, capaz de dar indicação sobre a espontaneidade ou
não espontaneidade de uma reacção. Para isso é necessário introduzir uma outra
grandeza termodinâmica denominada Entropia
ENTROPIA
Consideremos um gás contidas no recipiente. Se abrirmos a torneira que liga
os dois reservatórios, as partículas do gás distribuem-se pelos dois recipientes.
Este processo espontâneo ocorre quando eliminamos o constrangimento que
impede a passagem de gás de um para o outro lado.
Porque ocupam um volume maior, os
movimentos das partículas são mais
desordenados e distribuem-se por um
número maior de posições
∆H = 0
NOS PROCESSOS ESPONTÂNEOS HÁ DISPERSÃO DE ENERGIA
A energia flui de um estado inicial em que estava mais
concentrada para um estado final em que está mais dispersa.
A Propriedade Termodinâmica que traduz a dispersão de energia é a
Entropia, S
2ª LEI DA TERMODINÂMICA
UM PROCESSO ESPONTÂNEO CONDUZ A UM
AUMENTO DE ENTROPIA DO UNIVERSO
2ª Lei da Termodinâmica
uma reacção é espontânea se ∆S para o
universo é positivo.
∆Suniverso = ∆Ssistema + ∆Svizinhança
∆Suniverso > 0 para processos espontâneos
DISPERSÃO DE MATÉRIA E DE ENERGIA
A entropia (S) é uma medida do número de microestados disponíveis para as
partículas de um sistema, que aumenta com a desordem do sistema
isto é, num sistema ordenado o número de posições que cada partícula pode
ocupar é menor que num sistema desordenado
Quando o volume do recipiente aumenta,
aumenta o número de microestados:
A ENTROPIA AUMENTA
microestado: especifica um arranjo particular possível das partículas
Para uma mesma substância, a entropia depende do seu estado físico:
S (sólido) < S (líquido) << S (gás)
S˚(Br2 liq) < S˚(Br2 gas)
S˚(H2O sol) < S˚(H2O liq)
Entropia, S
O aumento da complexidade
molecular conduz, em geral, a
um aumento de entropia.
O número de microestados
possíveis aumenta
Entropia, S
Substância
S0 (J/K.mol)
S0[H2O(l)] é pequena devido às forças
intermoleculares fortes que existem entre
H2O(l)
69,9
H2O(g)
188,7
I2(s)
116,7
I2(g)
260,6
He(g)
126,1
Ne(g)
146,2
as moléculas.
S0[He(g)] é menor que a S0[Ne(g)] porque
as forças intermoleculares entre átomos de
Ne são mais fortes, uma vez que tem um
maior número de electrões que o He.
Entropia, S
Os líquidos ou sólidos dissolvem-se
espontaneamente num solvente devido
a um aumento de entropia.
No processo há dispersão de matéria (e
energia) em relação ao estado inicial
A ENTROPIA DE UM SISTEMA AUMENTA COM A TEMPERATURA
Um aumento de temperatura
causa
um
aumento
dos
movimentos moleculares que
resulta
num
aumento
entropia do sistema
de
3ª LEI DA TERMODINÂMICA
A ENTROPIA DE UM CRISTAL PERFEITO TENDE PARA ZERO À
MEDIDA QUE A TEMPERATURA TENDE PARA O ZERO ABSOLUTO
A entropia de uma substância a uma dada temperatura pode obter-se medindo
o calor necessário para aumentar a temperatura desde 0 K até essa
temperatura desde que o processo ocorra de forma reversível.
∆S = qrev/T
∆So
Para uma Reacção
=  So (productos) -  So (reagentes)
2 H2(g) + O2(g)
2 H2O(liq)
∆So = 2 So (H2O) - [2 So (H2) + So (O2)]
∆So = 2 mol (69.9 J/K·mol) [2 mol (130.7 J/K·mol) +
1 mol (205.3 J/K·mol)]
∆So = -326.9 J/K
Nesta reacção a variação de entropia é negativa porque 3 mol de gas dão 2
mol de líquido
2 H2(g) + O2(g)
∆So = -326.9 J/K
2 H2O(liq)
A variação de entropia do sistema é
negativa mas a reacção é espontânea
A variação de entropia do universo é positiva
∆Souniverso
?
Cálculo de ∆Souniverso
2 H2(g) + O2(g)
∆Souniverso = ∆Sosistema + ∆Sovizinhança
2 H2O(liq
∆Sovizinhança = qrev vizinhança / T
= -qrev sistema / T = - ∆Hosistema / T
∆Hosistema = 2 Hfo (H2O, l) - [2 Hfo (H2) + Hfo (O2)]
∆Hosistema = 2(-285.83) kJ/mol = -571.66 KJ/mol
∆Sovizinhança = 571.66x103 / (273.15+25) = 1917 J/K
∆Souniverso = 1917 - 327 = 1590 J/K
A ENTROPIA DO UNIVERSO AUMENTA
A REACÇÃO ESTÁ DESLOCADA
NO SENTIDO DA FORMAÇÃO
DOS PRODUTOS
Critérios de Espontaneidade
Lembre-se que
–∆H˚sis é proporcional a ∆S˚viz
Um processo exotérmico tem ∆S˚viz > 0.
RESUMO
processos espontâneos e sua relação com a entropia:
processos espontâneos tendem para o equilíbrio. São acompanhados por
um aumento de entropia
2ª Lei da Termodinâmica: a entropia do universo aumenta num
processo espontâneo
3ª Lei da Termodinâmica: a entropia de um cristal perfeito é zero a 0 k
entropia molar padrão: a entropia ganha quando se converte uma mole de uma
substância da sua forma de cristal perfeito a 0 K para as condições padrão (P = 1
atm; Concentração = 1M) à temperatura de 25 °C
A entropia é uma função de estado: DS = Sf ─ Si
Para uma reacção,
aA + bB
cC + dD
DSr0 = [cS0(C) + dS0(D)] ─ [aS0(A) + bS0(B)]
Se considerarmos o sistema e o meio exterior,
DSuniverso = DSsistema + DSmeio
De acordo com a 2ª lei da termodinâmica,
Num processo espontâneo, DSuniverso > 0
No equilíbrío, DSuniverso = 0
DSsistema = ─ DSmeio
A variação de entropia é directamente proporcional ao calor
fornecido ao sistema quando a temperatura sobe acima de 0 K
DS proporcional q
Por outro lado, a variação de entropia do meio depende da sua temperatura, isto é,
se
Tmeio elevada
DS é pequeno
A variação de entropia é inversamente
Tmeio baixa
DS é grande
proporcional à temperatura
DSmeio =
─ DHsistema
T
qmeio = ─ DHsist
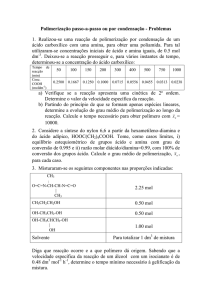
PROBLEMAS
1. Quando aquecido, o (NH4)2Cr2O7(s) decompõe-se para dar origem a N2(g), H2O(g)
e Cr2O3(s).
a) Escreva e acerte a equação química que traduz a reacção.
b) Preveja se a variação de entropia da reacção é positiva ou negativa. Justifique.
2. Calcule, à temperatiura de 25 °C e à pressão de 1atm, a variação de entropia da
reacção
N2(g) + 2O2(g)
2NO2(g)
b) calcule a variação de entropia correspondente à conversão de 40,00 g de N 2(g)
e 91,38 g de O2(g) em 131,38 g de NO2(g).
S0(N2) = 191,50 Jmol─1K─1; S0(O2) = 205,03 Jmol─1K─1; S0(NO2) = 239,95 Jmol─1K─1
PROBLEMAS
3. Calcule a variação de entropia da reacção
CH4(g)
C(s, gr) + 2H2(g)
quando 26,71 g de CH4(g) reagem para dar 20,00 g de grafite e 6,71 g de H 2(g) à
temperatiura de 25 °C e à pressão de 1atm.
S0(CH4) = 186,15 Jmol─1K─1; S0(C,gr) = 5,74 Jmol─1K─1; S0(H2) = 130,57 Jmol─1K─1
PROBLEMAS
4. Considere a reacção de síntese do amoníaco,
N2(g) + 3H2(g)
2NH3(g)
DH0 = ─92,6 kJ
a) calcule DSr0
b) diga se a reacção é espontânea, a 25 °C.
S0(N2) = 191,50 Jmol─1K─1; S0(H2) = 130,57 Jmol─1K─1; S0(NH3) = 192,34 Jmol─1K─1
NOTA: Embora a 2ª Lei da Termodinâmica nos diga que a reacção é espontânea
porque DSuniverso é positivo, a 25 °C não se forma NH3 porque a cinética da reacção
é lenta, isto é, a velocidade da reacção nessas condições é muito pequena.
Energia Livre de Gibbs, G
∆Suniv = ∆Sviz + ∆Ssis
DSuniv =
DHsys
T
+ DSsys
J. Willard Gibbs
Se multiplicarmos por -T
1839-1903
-T∆Suniv = ∆Hsis - T∆Ssis
-T∆Suniv = variação da energia de Gibbs do
sistema = ∆Gsistema
Em condições padrão —
∆Gosis = ∆Hosis - T∆Sosis
Num processo espontâneo,
∆Suniv = ∆Sviz + ∆Ssis >0
∆Gosis = ∆Hosis - T∆Sosis <0
Um processo que ocorre à temperatura T é espontâneo
quando as variações de entalpia e de entropia são tais
que DH ─ TDS < 0
o
∆G
=
o
∆H
-
o
T∆S
Variação da energia de Gibbs =
variação de energia total do sistema - energia perdida
na dispersão de energia
Se a reacção é
• exotérmica (∆Ho negativo) e a entropia aumenta (∆So
positivo )
• logo, ∆Go é NEGATIVO
• A reacção é espontânea (product-favored).
o
∆G
=
o
∆H
-
o
T∆S
Se a reacção é
• endotérmica (∆Ho positive)
• e a entropia diminui (∆So negative)
• Então ∆Go é POSITIVO
• A reacção é não-espontânea (isto é, reactant-favored).
Energia de Gibbs, G
∆Go = ∆Ho - T∆So
∆Ho
∆So
∆Go
Reacção
exo(–)
aumento(+)
–
Prod-favored
endo(+)
diminuição(-)
+
React-favored
exo(–)
diminuição(-)?
Dependente T
endo(+)
aumento (+)?
Dependente T
Energia de Gibbs, G
∆Go = ∆Ho - T∆So
2 métodos para calcular ∆Go
a)Determinar ∆rHo e ∆rSo e usar a equação
de Gibbs.
b)Usar valores tabulados de energias livres
de formação, ∆fGo.
∆rGo =  ∆fGo (produtos) -  ∆fGo (reagentes)
Define-se DG0 , variação de energia de Gibbs padrão, como a variação de energia de
energia de Gibbs de uma reacção efectuada em condições padrão.
Define-se DGf0 , energia de Gibbs de formação padrão, como a variação de energia
de energia de Gibbs que corresponde à síntese de uma mole de um composto a
partir dos seus elementos no estado padrão.
Para uma reacção,
aA + bB
cC + dD
DGr0 = Σ nDGf0(produtos) ─ mDGf0(reagentes)
onde n e m são os coeficientes estequiométricos
Cálculo de ∆Gorxn
∆rGo =  ∆Gfo (produtos) -  ∆Gfo (reagentes)
C(grafite) + O2(g)
CO2(g)
∆rGo = ∆fGo(CO2) - [∆fGo(graf) + ∆fGo(O2)]
∆rGo = -394.4 kJ - [ 0 + 0]
∆rGo = -394.4 kJ
A reacção é product-favored
Para um elemento ou para um composto elementar no estado padrão ∆fG˚ = 0
Energia de Gibbs e Temperatura
2 Fe2O3(s) + 3 C(s)
4 Fe(s) + 3 CO2(g)
∆rHo = +467.9 kJ
∆rSo = +560.3 J/K
∆rGo = +300.8 kJ
A reacção não ocorre a 298 K
A que temperatura é que a reacção é possível? Isto é, a que
temperatura o valor de ∆rGo passa de (+) para (-)?
∆rGo = 0 = ∆rHo - T∆rSo
T=
Dr H
Dr S
=
467.9 kJ
= 835.1 K
0.5603 kJ/K
ENERGIA DE GIBBS E EQUILÍBRIO QUÍMICO
Quando não estamos em condições padrão, por exemplo durante uma reacção
(mesmo que no início os reagentes e produtos estejam nas condições padrão elas
variam ao longo do tempo),
DG = DG0 + RT lnQ
onde Q representa o quociente reaccional
Em qualquer instante define-se quociente reaccional, Q, como a razão entre as
concentrações de produtos e reagentes no instante considerado.
No equilíbrio,
Q = Keq e DG = 0
A expressão
DG = DG0 + RT lnQ
transforma-se em
DG0 = ─RT lnK
Substituindo DG0 na expressão anterior obtém-se
DG = ─RT lnK + RT lnQ
DG = RT ln
Q
K
Calcular Keq
∆rGo = - RT lnK
Para a reacção N2O4
2 NO2
∆rGo = +4.8 kJ
∆rGo = +4800 J = - (8.31 J/K)(298 K) ln K
4800 J
ln K = = -1.94
(8.31 J/K)(298K)
K = 0.14
∆rGo > 0
K<1
∆G, ∆G˚ e Keq
• ∆G é a variação de energia livre em condições
não-padrão
• ∆G está relacionado com ∆G˚
• ∆G = ∆G˚ + RT ln Q
onde Q = quociente reaccional
• Quando Q < K or Q > K, a reacção é espontânea
• Quando Q = K a reacção está no equilíbrio
• Quando ∆G = 0 a reacção está no equilíbrio
• Logo, ∆G˚ = - RT ln K
Product Favored, ∆G˚ negative, K > 1
Reactant Favored, ∆G˚ positive, K < 1
Q<K
DG = RT ln
Q
K
<0
a reacção evolui no sentido directo
Q=K
DG = RT ln
Q
K
=0
a reacção atingiu o equilíbrio
Q>K
DG = RT ln
Q
K
>0
a reacção evolui no sentido inverso
K >> 1
DG0 < 0
em condições padrão a é espontânea
(product favored)
K >> 1
DG0 = 0
em condições padrão a reacção
está no equilíbrio
K >> 1
DG0 > 0
em condições padrão a reacção
não é espontânea (reactant favored)
PROBLEMAS
1. A variação da energia de Gibbs padrão para a reacção
3NO(g)
N2O(g) + NO2(g)
é ─104,18 kJ. Calcule a constante de equilíbrio da reacção a 25 °C.
2. Calcule as constantes de equilíbrio para a reacção inversa à do problema 1 e
para a reacção inversa à do problema 1 multiplicada por ½.
Compare os resultados obtidos.
3. Calcule a variação de energia de Gibbs para a reacção do problema 1, a 25 °C,
quando as pressões parciais dos três gases são 0,0010 atm.
4. Calcule a constante de equilíbrio a 25 °C para a seguinte reacção
2H2O(l)
Comente o resultado obtido.
Dados: DHf0[H2O(l)] = ─237,2 kJ/mol
2H2(g) + O2(g)