CENTRO DE ENSINO SUPERIOR DO AMAPÁ Coordenação de

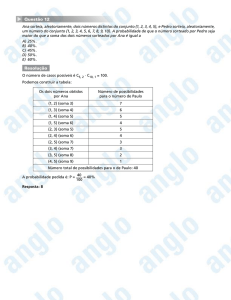
CENTRO DE ENSINO SUPERIOR DO AMAPÁ
Coordenação de Ciências Contábeis
Probabilidades
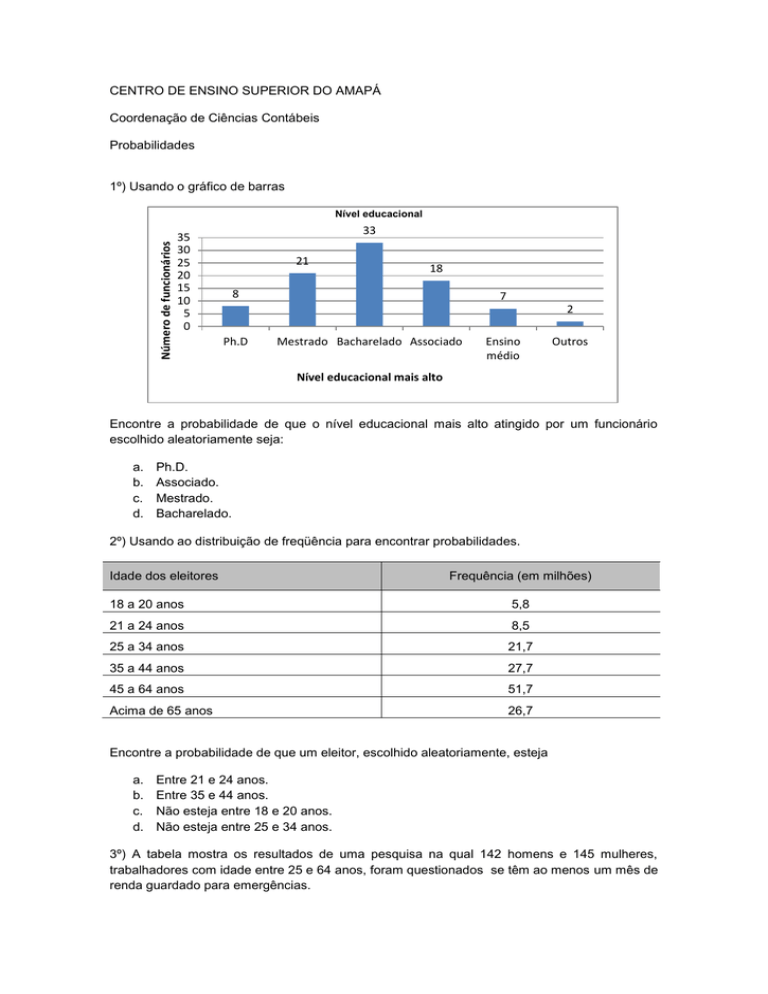
1º) Usando o gráfico de barras
Número de funcionários
Nível educacional
33
35
30
25
20
15
10
5
0
21
18
8
7
2
Ph.D
Mestrado Bacharelado Associado
Ensino
médio
Outros
Nível educacional mais alto
Encontre a probabilidade de que o nível educacional mais alto atingido por um funcionário
escolhido aleatoriamente seja:
a.
b.
c.
d.
Ph.D.
Associado.
Mestrado.
Bacharelado.
2º) Usando ao distribuição de freqüência para encontrar probabilidades.
Idade dos eleitores
Frequência (em milhões)
18 a 20 anos
5,8
21 a 24 anos
8,5
25 a 34 anos
21,7
35 a 44 anos
27,7
45 a 64 anos
51,7
Acima de 65 anos
26,7
Encontre a probabilidade de que um eleitor, escolhido aleatoriamente, esteja
a.
b.
c.
d.
Entre 21 e 24 anos.
Entre 35 e 44 anos.
Não esteja entre 18 e 20 anos.
Não esteja entre 25 e 34 anos.
3º) A tabela mostra os resultados de uma pesquisa na qual 142 homens e 145 mulheres,
trabalhadores com idade entre 25 e 64 anos, foram questionados se têm ao menos um mês de
renda guardado para emergências.
Homens
Mulheres
Total
Menos de um mês de renda
66
83
149
Um mês de renda ou mais
76
62
138
Total
142
145
287
a. Encontre a probabilidade de que um trabalhador selecionado aleatoriamente tenha um
mês de renda ou mais guardada para emergências.
b. Dado que um trabalhador selecionado aleatoriamente é homem, encontre a
probabilidade de que o trabalhador tenha menos de um mês de renda guardada.
c. Dado que um trabalhador selecionado aleatoriamente tenha um mês ou mais de renda
guardada, encontre a probabilidade de que o trabalhador seja mulher.
d. Os eventos “ter menos de um mês de renda guardada” e “ser homem” são
dependentes ou independentes? Explique.
4º) A tabela mostra o número de estudantes, homens e mulheres, matriculados no curso de
enfermagem da Universidade de Oklahoma em um semestre recente;
Curso de
Outros
Total
Enfermagem
cursos
Homens
95
1.015
1.110
Mulheres
700
1.727
2.427
Total
795
2.742
3.537
a. Encontre a probabilidade de que um estudante selecionado aleatoriamente seja
estudante de enfermagem.
b. Encontre a probabilidade de que um estudante selecionado aleatoriamente seja
homem.
c. Encontre a probabilidade de que um estudante selecionado aleatoriamente seja
estudante de enfermagem, dado que o estudante seja homem.
d. Encontre a probabilidade de que um estudante selecionado aleatoriamente seja
estudante de enfermagem e homem.
e. Os eventos de ser um estudante homem e ser estudante de enfermagem são
dependentes ou independentes? Explique.
5º) Na amostra de 1.000 pessoas (525 homens e 475 mulheres), 113 são canhotas (63 homens
e 50 mulheres). Os resultados da amostra são mostrados na tabela. Uma pessoa é
selecionada aleatoriamente. Encontre a probabilidade de cada evento.
Sexo
a.
b.
c.
d.
e.
Homem
Mulher
Total
Mão
Esquerda
63
50
113
Dominante
Direita
462
425
887
Total
525
475
1.000
A pessoa é canhota ou mulher.
A pessoa é destra ou homem.
A pessoa não é destra ou homem.
A pessoa é uma mulher destra.
Os eventos “ser destro” e “ser mulher” são mutuamente exclusivos? Explique.
Use a tabela para determinar a probabilidade do evento
Número de funcionários
0a4
5a9
10 a 19
20 a 99
100 ou mais
Porcentagem de firmas
60,8%
17,7%
10,8%
8,9%
1,8%
6º) Qual a probabilidade de que uma empresa selecionada aleatoriamente tenha pelo menos
10 funcionários.
7º) Qual a probabilidade de que uma empresa selecionada aleatoriamente no mínimo 5 e
menos de 99 funcionários?
8º) Qual a probabilidade de que uma empresa selecionada aleatoriamente tenha menos que 20
funcionários?
9º) Um carregamento de 150 televisores tem 3 unidades, defeituosas. Determine de quantas
maneiras a empresa de vendas pode comprar três dessas unidades e receber (a) nenhum item
defeituoso, (a) todos os itens defeituosos e (c) pelos menos uma unidade sem defeito.
10º) Um lote com 350 bilhetes de rifa tem 4 bilhetes ganhadores. Você compra 4 bilhetes; qual
a probabilidade de que você tenha:
a.
b.
c.
d.
Nenhum bilhete vencedor.
Todos vencedores
Pelo menos um vencedor.
Pelo menos um que não seja vencedor.
11º) Uma loja dispõe de 12 geladeiras do mesmo tipo, das quais 4 apresentam defeitos.
a. Se um freguês vai comprar uma geladeira, qual a probabilidade de levar uma
defeituosa?
b. Se um freguês vai comprar duas geladeiras, qual a probabilidade de levar duas
defeituosas?
c. Se um freguês vai comprar duas geladeiras, qual a probabilidade de levar pelo menos
uma defeituosa?
12º) Um lote é formado por 10 peças boas, 4 com defeitos e 2 com defeitos graves. Uma peça
é escolhida ao acaso. Calcule a probabilidade de que:
a. Ela não tenha defeitos graves;
b. Ela não tenha defeitos;
c. Ela seja boa ou tenha defeitos graves.
13º) Considere o mesmo lote do problema anterior. Retiram-se 2 peças ao acaso. Calcule a
probabilidade de que:
a.
b.
c.
d.
Ambas sejam perfeitas;
Pelos menos uma seja perfeita;
Nenhuma tenha defeitos graves;
Nenhuma seja perfeita.
Esta lista de exercício juntamente com os exemplos trabalhados na sala servirão de
base para a avaliação que ocorrerá dia 26/09/2011