7ª Queda Livre, Lançamento Vertical, Velocidade

(Queda Livre, Lançamentos Verticais, velocidade media, mru, mruv, derivada e integrais)
Movimento vertical
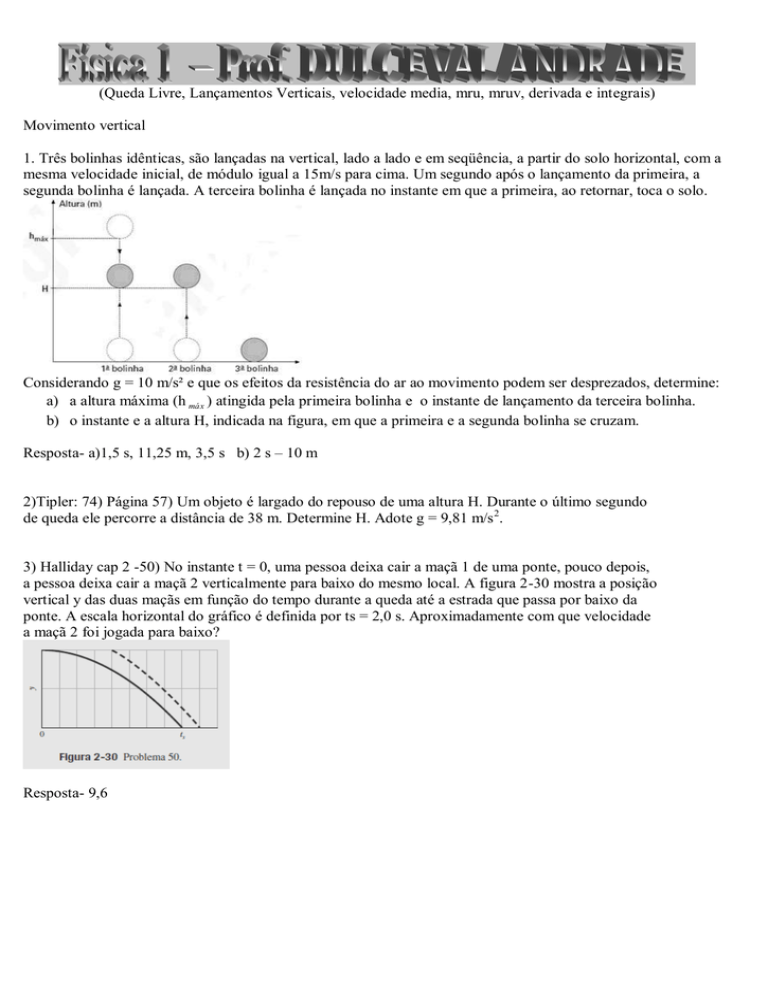
1. Três bolinhas idênticas, são lançadas na vertical, lado a lado e em seqüência, a partir do solo horizontal, com a
mesma velocidade inicial, de módulo igual a 15m/s para cima. Um segundo após o lançamento da primeira, a
segunda bolinha é lançada. A terceira bolinha é lançada no instante em que a primeira, ao retornar, toca o solo.
Considerando g = 10 m/s² e que os efeitos da resistência do ar ao movimento podem ser desprezados, determine:
a) a altura máxima (h máx ) atingida pela primeira bolinha e o instante de lançamento da terceira bolinha.
b) o instante e a altura H, indicada na figura, em que a primeira e a segunda bolinha se cruzam.
Resposta- a)1,5 s, 11,25 m, 3,5 s b) 2 s – 10 m
2)Tipler: 74) Página 57) Um objeto é largado do repouso de uma altura H. Durante o último segundo
de queda ele percorre a distância de 38 m. Determine H. Adote g = 9,81 m/s 2.
3) Halliday cap 2 -50) No instante t = 0, uma pessoa deixa cair a maçã 1 de uma ponte, pouco depois,
a pessoa deixa cair a maçã 2 verticalmente para baixo do mesmo local. A figura 2-30 mostra a posição
vertical y das duas maçãs em função do tempo durante a queda até a estrada que passa por baixo da
ponte. A escala horizontal do gráfico é definida por ts = 2,0 s. Aproximadamente com que velocidade
a maçã 2 foi jogada para baixo?
Resposta- 9,6
4) Halliday cap 2-56) A figura 2-32 mostra a velocidade v em função da altura y para uma bola
lançada verticalmente para cima ao longo de um eixo Y. A distância d é 0,40 m. A velocidade na
altura yA é VA. A velocidade na altura yB é VA/3. Determine a velocidade VA.
Sugestão – coloque o eixo para cima e use Torricelli – Resposta-3,0
Página 36:
60) Uma pedra é lançada verticalmente para cima a partir do solo no instante t = 0. Em t = 1,5 s, a
pedra ultrapassa o alto de uma torre; 1,0 s depois atinge a altura máxima. Qual é a altura da torre?
Resposta- 20,4 m.
VELOCIDADE MEDIA.
1) Um motorista pretende percorrer, em 4,5 horas, a distância de 360 km. Todavia, dificuldades
imprevistas obrigam-no a manter a velocidade de 60 km/h durante os primeiros 150 minutos. No
percurso restante, para chegar no tempo previsto, ele deverá manter a seguinte velocidade média:
a) 90 km/h. b) 95 km/h.
c) 100 km/h.
d) 105 km/h.
e) 110 km/h.
Resposta da questão 1: [D]
2) Dois trens, ambos se movendo com velocidade de 30 km/h, trafegam em sentidos opostos na mesma linha
férrea retilínea. Um pássaro parte da extremidade dianteira de um dos trens, quando estão separados por 60 km,
voando a 60 km/h, e se dirige em linha reta para outro trem. Ao chegar ao outro trem, o pássaro faz meia volta e
se dirige para o primeiro trem, e assim por diante. Qual a distância que o pássaro até os dois trens colidirem?
Resposta- 60 km
3) Tipler questão 53- pag56 ( valores modificados): O Guepardo pode correr até 100 km/h, o Falcão
pode voar até até 150 km/h e o Marlim pode nadar até 100 km/h. Os três participam, como equipe, de
uma corrida de revezamento, cada um cobrindo uma distância L com sua rapidez máxima. Qual é a
rapidez média desse time para todo o percurso?
Lembre-se dos problemas de trechos iguais. Neste caso três trechos.
4) A velocidade média de um automóvel que durante os primeiros 150 km de viagem deslocou-se a
50 km/h e nos 700 km seguintes a 100 km/h, é:
a) 55 km/h
b) 60 km/h
c) 65 km/h
d) 85 km/h e) 70 km/h
5) Um carro se desloca entre duas cidades em duas etapas. Na primeira etapa desloca-se com
velocidade média de 80 km/h durante 3,5 h. Após permanecer parado por 2,0 horas, o carro percorre
os 180 km restantes com velocidade média de 40 km/h. A velocidade média do carro no percurso
entre as duas cidades foi, em km/h,
a) 40
b) 46
c) 64
d) 70
e) 86
MRU
1) Duas estações A e B estão separadas por 200 km, medidos ao longo da trajetória. Pela estação A
passa um trem P, no sentido de A para B, e simultaneamente passa por B um trem Q, no sentido de B
para A. Os trens P e Q têm movimentos uniformes com velocidades de valores absolutos 70 km/h e
30 km/h, respectivamente. Determine o instante do encontro.
Resposta- 2 h - Sugestão – escreva a função horária e iguale as funções. Não esqueça que uma das velocidades
será negativa.
2) Dois carros viajam ao longo de uma estrada reta. O carro A mantém uma rapidez constante de 80
km/h e o carro B mantém uma rapidez constante de 110 km/h. Em t=0, o carro B está 45 km atrás do
carro A.
A) Quanto mais viajará o carro A até ser ultrapassado pelo carro B?
B) Quanto à frente do carro A estará o carro B 30 s após tê-lo ultrapassado?
Resp. A) 1.2 105 m
B) 0.25 km
3) (a) Se a posição de uma partícula é dada por x = 4 - 12t + 3t2 (onde t está em segundos e x
está em metros), qual é a sua velocidade em t =1 s?
(b) Ela está se deslocando no sentido positivo ou negativo de x neste exato momento?
(c) Qual é o módulo da sua velocidade neste mesmo instante?
(d) O módulo da velocidade é maior ou menor em instantes posteriores?
(e) Determine sua velocidade media no intervalo de de t0=0 a t= 2s.
4) Um trem parte do repouso e se move com aceleração constante. Em um determinado instante,
ele viaja a 30 m/s e, 160 m adiante, trafega a 50 m/s. Calcule (a) a aceleração, (b) o tempo
necessário para percorrer os 160 m mencionados, (e) o tempo necessário para atingir a
velocidade de 30 m/s e (d) a distância percorrida desde o repouso até o instante em que sua
velocidade era de 30 m/s.
5) Uma partícula tinha uma velocidade de v = 18 m/s na direção do eixo x, em um certo tempo, e
2,4 s depois sua velocidade era de 30 m/s no sentido contrário. Quais eram o modulo e o sentido da
aceleração média da partícula durante este intervalo de 2,4 s ?
6) Um múon (uma partícula elementar) entra em uma região com uma velocidade de 5,00.10 6
m/s e depois é desacelerado a uma taxa de 1,25.1014 m/s2. Qual a distância que o múon percorre
até parar?
7) Um elétron possui uma aceleração constante de +3,2 m/s2. Em um certo instante sua
velocidade é de + 9,6 m/s. Qual é a sua velocidade (a) 2,5 s antes e (b) 2,5 s depois?
8) Halliday-37) A figura mostra o movimento de uma partícula que se move ao longo do eixo x com
aceleração constante.
A escala vertical do gráfico é definida por xs = 6,0 m. Quais são:
a) O módulo da velocidade? B) O módulo da aceleração da partícula.
Sugestão- escreva duas equações espaço do MRUV e monte um sistema. Observe que a posição
inicial e - 2 m
Resposta-a) 0 e b) 4 positivo
9) Tipler 84: Página 58) Dois trens viajam em sentidos opostos, em trilhos paralelos. Eles estão
inicialmente em repouso e suas frentes estão distantes 40 m. O trem a esquerda acelera para a direita a
1,0 m/s2. O trem a direita acelera para a esquerda a 1,3 m/s2. A) Determine o instante de encontro.
B)Qual a distância percorrida pelo trem da esquerda ate que as frentes dos trens se cruzem?
Respostas-3) Resp. (a) v (1s) = - 6 m/s i; (b) negativo; (c) v = 6 m/ s; (d) diminui; (e)
sim, t =2 s 4) Resp. (a) a = 5 m/s2; (b) t = 4 s; (c) t = 6 s e (d) x = 90 m. 5) Resp. a = 20 ms-2 i 6) Resp. x = 0,1 m 7) Resp. (a) v = 1,6 m/s e (b) v = 17,6 m/s.
DERIVADAS.
1) A posição de um móvel em movimento retilíneo é dada por x(t) = t3 – 9t2 + 1,5t onde, t está em
segundo e x em metros.
a) Determine a posição do móvel em t = 6 s.
b) Determine a velocidade media durante o intervalo de 0 a 6 s.
Determine a velocidade instantânea em t = 2 s.
c) O movimento e MRU- MRUV ou MV – Justifique.
2) Dado que x(t) = 10 + 1,5t - 1,5 t2 + t3/3 determine
A) a função velocidade
B) a função aceleração.
3) Um ponto material move-se alo longo de uma trajetória horizontal com a posição dada por:
x(t) = t3 - 3 t2 determine a distância percorrida pelo móvel em 3,5 segundos de movimento.
4) Um movimento é dado pela expressão x(t) = 10 – 2t + ½ t2 onde a posição é medida em metros e
t em segundos. Determine: a) A equação da velocidade instantânea em função do tempo;
b) Verifique se o móvel muda de sentido, se mudar, determine a posição em que isto ocorre;
c) Em que instante o móvel passa pela origem, se isso acontecer;
d) Qual o aspecto do gráfico da posição em função do tempo, e da velocidade em função do tempo.
Resp. a) v (t) = -2 + t ; b) sim, t = 2 s e x = 8 m e c) nunca.
5) A posição de um móvel ao longo de uma linha reta é dada pela função: x(t) = 3,0t3 –10,0t2 + 9,0 t ;
Onde t é dado em segundos e x em metros (SI). Sabendo que a velocidade instantânea é dada pela
derivada da posição em relação ao tempo e que geometricamente, esta derivada é representada pela
inclinação da reta tangente ao gráfico da posição em função do tempo. Determine para o intervalo de
tempo entre 0 ⋜ t ⋜ 10,0 s:
a) Qual a equação da velocidade instantânea em função do tempo?
c) Em que instantes, se ocorrer, a velocidade do móvel é zero?
e) Qual a velocidade média no intervalo de tempo de t = 3 s a t = 6 s?
INTEGRAL
1) Considere que um estudante está dirigindo um carro em um trecho retilíneo de uma. No tempo t =
0, quando ele está se movendo a 10 m/s no sentido positivo do eixo “x”, ele passa por um poste de
sinalização que indica uma distância de 50 m. Sabendo que a aceleração em função do tempo é dada
por: a(t) = 2,0 m/s2 – 0,10 m/s2 t .
a) Deduza uma expressão para V(t) e X(t).
b) Determine a velocidade para t = 2 s. c) Onde está o carro quando a t = 3 s
2) A aceleração de um ônibus é dada por a(t) = αt, onde α = 1,2 m/s3.
a) Se a velocidade do ônibus para t = 1,0 s é igual a 5,0 m/s, qual é sua velocidade para t = 2,0 s?
b) Se a posição do ônibus para t= 1,0 s é igual a 6,0 m, qual sua posição para t = 2,0 s?
3) A aceleração de uma motocicleta é dada por a(t) = At – Bt2, onde A = 1,5 m/s3 e B = 0,12 m/s4. A
motocicleta está em repouso na origem no instante t = 0s. Calcule sua velocidade e posição em função
do tempo.