UFES Centro Universitário Norte do Espírito Santo

Universidade Federal do Espírito Santo - UFES
Centro Universitário Norte do Espírito Santo - CEUNES
APOSTILA
Disciplina: Expressão Gráfica
Curso: Agronomia
Professor: Sidney Sára Zanetti
São Mateus - ES
2010
Expressão Gráfica
UFES / CEUNES
APOSTILA DA DISCIPLINA DE EXPRESSÃO GRÁFICA
1) INTRODUÇÃO
A computação revolucionou a utilização da expressão gráfica no exercício da
engenharia, viabilizando a execução de trabalhos tridimensionais, que antes só eram
possíveis através da construção de modelos.
Os softwares existentes no mercado possibilitam a construção de modelos virtuais,
cujas imagens são muito próximas do real, onde se podem ver, em três dimensões, todos os
detalhes de uma máquina, de um equipamento ou até mesmo de um processo inteiro. Estes
modelos virtuais possuem recursos de cores, textura e animação onde as imagens podem
ser giradas, cortadas, alteradas e ao mesmo tempo compartilhadas por meio de redes, ou
da internet, por todas as partes envolvidas no desenvolvimento de estudos e projetos.
A computação gráfica, com certeza facilitou e ampliou o desenvolvimento de projetos
na área da engenharia e da arquitetura porque, além de poder ser utilizada integrada com
softwares de cálculos ou com banco de dados, os modelos virtuais são fáceis de serem
compreendidos e enchem os olhos de quem está comprando o projeto.
No entanto, a execução dos projetos das áreas da engenharia e da arquitetura ainda
dependente dos desenhos bidimensionais que são utilizados para fazer o detalhamento dos
detalhes construtivos que envolvem o objeto projetado. Assim, apesar de todos os recursos
propiciados pela computação gráfica, o exercício da engenharia ainda está diretamente
vinculado à leitura e interpretação de desenhos bidimensionais, utilizando-se os recursos
de desenhos técnicos.
Pode ser que no futuro todos os problemas gráficos da engenharia sejam elaborados em
três dimensões, mas ainda não é hora para se abandonar a linguagem bidimensional.
Diferentemente das imagens tridimensionais, que podem ser entendidas por qualquer
pessoa, os desenhos bidimensionais se constituem em uma linguagem gráfica que só pode
ser entendida por quem a estuda.
Para os cursos que visam a preparação para atividades de desenvolvimento de projetos,
é importante o treinamento utilizando softwares CAD (Computer Aided Design), que
viabilizam a elaboração de desenhos/projetos auxiliados pelo computador.
2) NORMALIZAÇÃO E PADRONIZAÇÃO DO DESENHO TÉCNICO
A padronização dos procedimentos de representação gráfica permite transformar o
Desenho Técnico em uma linguagem gráfica. Essa padronização é feita através de normas
técnicas que são seguidas e respeitadas internacionalmente.
No Brasil as normas são aprovadas e editadas pela Associação Brasileira de Normas
Técnicas – ABNT, fundada em 1940. No âmbito internacional foi criada, em 1947, a
Organização Internacional de Normalização (International Organization for
Standardization – ISO). Quando uma norma técnica proposta por qualquer país membro é
aprovada por todos os países que compõem a ISO, essa norma é organizada e editada como
norma internacional.
No Brasil as normas técnicas que regulam o Desenho Técnico são editadas pela ABNT,
registradas pelo INMETRO (Instituto Nacional de Metrologia, Normalização e Qualidade
Industrial), como Normas Brasileiras Revisadas (NBR), em consonância com as normas
internacionais aprovadas pela ISO.
Para o desenho técnico existem várias normas publicadas em diferentes épocas, onde os
principais aspectos abordados são tamanhos e formatos de papéis, escalas, letras e
algarismos, linhas, legendas, etc. A norma NBR 5984 – Norma geral de desenho técnico
(antiga NB 8) foi aprovada em 1950 e revisada várias vezes tendo como objetivos fixar as
condições gerais que devem ser observadas na execução dos desenhos técnicos. Entretanto,
esta norma foi substituída por diversas outras, estando algumas listadas abaixo:
1
Expressão Gráfica
UFES / CEUNES
NBR 10647 - Desenho técnico - Terminologia
NBR 10067 - Princípios gerais de representação em desenho técnico
NBR 10068 - Folha de desenho - Leiaute e Dimensões
NBR 10582 - Apresentação da folha para desenho técnico
NBR 8402 - Execução de caracter para escrita em desenho técnico
NBR 8403 - Aplicação de linhas em desenhos
NBR 8196 - Desenho técnico - Emprego de escalas
NBR 10126 - Cotagem em desenho técnico
NBR 13142 - Desenho técnico - Dobramento de cópia
NBR 12298 - Representação de área de corte por meio de hachuras em desenho técnico
3) INSTRUMENTALIZAÇÃO – TIPO, MANUSEIO E MANUTENÇÃO
Para a disciplina de Expressão Gráfica aconselha-se o uso de instrumentos de precisão e
qualidade, o que existe com grande variedade no mercado. Para cada tipo de desenho
existem também instrumentos mais específicos.
Atualmente com os sistemas de CAD o uso de certos instrumentos deixa quase de ser
necessário, por sua vez para condução da disciplina de Expressão Gráfica recomenda-se
adquirir e trazer em todas as aulas papel no formato A3, lapiseira 0,5 ou 0,7 mm, régua T,
borracha branca, fita adesiva, flanela de algodão, transferidor, compasso, régua
milimetrada e transparente.
A seguir tem-s e a descrição detalhada de cada equipamento:
Prancheta (mesa para desenho) - Equipamento importante para o desenho técnico. Pode
ser de madeira com alavancas de acionamento da inclinação e da altura. Facilita a execução
do desenho.
Papel - Existem diversos tipos de papel para desenho. Para desenho a mão com uso de
lápis é aconselhável utilizar papel opaco (sulfite) ou transparente (manteiga). Para
desenhos definitivos recomenda-se o papel-vegetal empregando caneta nanquim. Com o
uso de computador para a elaboração do projeto é comum o uso do papel sulfite para
impressão.
Régua T - São empregadas no traçado de linhas horizontais e apoio aos esquadros para o
traçado de linhas inclinadas ou verticais. São fabricadas de madeira com bordas de plástico
inquebrável ou acrílico (Figura 1).
Obs: No traço com a régua T deve-se começar a traçar da esquerda para a direita, de modo
que a mão não fique em cima do que já foi desenhado (Figura 2).
Figura 1 – Exemplo de uma régua T.
2
Expressão Gráfica
UFES / CEUNES
Figura 2 – Esquema de traçado com régua T.
Régua paralela – Utilizada em substituição à régua T (Figura 3).
Figura 3 – Esquema ilustrativo de régua T e régua paralela.
Esquadros - Utilizados no traçado de linhas inclinadas ou perpendiculares a régua T.
Existem dois tipos de esquadros: na forma de triângulo isósceles (2 ângulos de 45º e um de
90º) e na forma de triângulo escaleno (ângulos de 30º, 60º, e 90º). A combinação ideal para
uso seria aquela em que o cateto do esquadro de 30/60º seja igual a hipotenusa do
esquadro de 45º. A combinação de esquadros permite que sejam traçadas linhas formando
múltiplos de 15º.
Compasso - Traçar circunferências ou arcos de circunferências.
Transferidores - Instrumentos para a medição de ângulos. Comercialmente existem
modelos de 0 a 180º e de 0 a 360º.
3
Expressão Gráfica
UFES / CEUNES
Réguas flexíveis ou curvas francesas - Curvas não traçadas pelo compasso (raio
indefinido).
Normógrafos e gabaritos - Empregados no auxílio à escrita e desenhos.
Canetas - nanquim (para desenhos definitivos)
Lápis (lapiseira) e Grafite:
H a 6H: consistência de dura a extremamente dura.
B a 6B: consistência de macia a extremamente macia.
Obs.: uso mais comum: B, HB e H.
4) FORMATOS E TAMANHOS DE PAPEL
O formato básico do papel, designado por A0 (A zero), é o retângulo cujos lados medem
841 mm e 1.189 mm, tendo a área de 1m2. Do formato básico, derivam os demais formatos
da série A (Figura 4), pela bipartição ou duplicações sucessivas, segundo uma linha
perpendicular ao maior lado do retângulo.
Figura 4 – Formatos de papel da série A.
Os formatos da série A, de A0 a A4, têm as dimensões indicadas no quadro a seguir. As
folhas não recortadas devem ter as dimensões mínimas indicadas na última coluna do
quadro. Na Tabela 1 têm-se as especificações técnicas de cada formato.
4
Expressão Gráfica
UFES / CEUNES
Tabela 1 – Formatos da série A
Formato
(mm)
A0
A1
A2
A3
A4
Linha de corte
(mm)
841 x 1189
594 x 841
420 x 594
297 x 420
210 x 297
Margem (mm)
Esquerda
Direita
25
10
25
10
25
7
25
7
25
7
5) CALIGRAFIA TÉCNICA
Os textos e algarismos representados em desenho técnico (Figura 5) seguem normas
que garantem a legibilidade e uniformidade. Podem ser escritos utilizando-se o normógrafo
ou à mão livre. A norma NBR 6492/1994 recomenda letras maiúsculas não inclinadas,
assim como os números, medindo de 3 a 5 mm. O espaçamento entre as linhas não deve ser
inferior a 2 mm.
Figura 5 - Textos e algarismos representados em desenho técnico.
6) CARIMBO – CONTEÚDO E TRAÇADO
O carimbo ou rótulo deve acompanhar todo desenho e serve tanto para a identificação
como para conter informações sobre o conteúdo do desenho. O carimbo deve ser inserido
no canto inferior direito da folha de desenho. Em geral o carimbo deve conter as seguintes
informações: nome; título do projeto; nome do projetista; nome do desenhista; data;
escalas; nome do cliente; e local para assinaturas.
Exemplo 1 (Uso para trabalhos acadêmicos)
Disciplina: Desenho Técnico
Título: Projeções Ortogonais
Aluno: Fulano de Tal
Escala: 1:50
Data: 15/08/07
Turma: A
Matrícula: 123456
Exemplo 2 (Projetos rurais)
Projeto: Construção Rural
Denominação: Sala de ordenha
Localização: Faz. Bela Vista,
BR 101 km 74
São Mateus, ES
Proprietário: Marco Rosa
Responsável: Escala: 1:100
Eng° Agr° Paulo Sousa
CREA 01234586
Obra no 013/03
Arquivo no PROJ/01
Data: 15/08/07
Áreas (m2)
Construída ..... 89,2
Livre .............. 65,1
Total ............. 154,3
Escala: 1:100
Registros
5
Expressão Gráfica
UFES / CEUNES
7) NOMENCLATURA DE LINHAS – CLASSIFICAÇÃO E HIERARQUIA
O desenhista deve empregar diferentes tipos de linhas objetivando a diferenciação na
apresentação do desenho. As linhas podem ser diferenciadas quanto ao tipo e a espessura,
conforme apresentado a seguir:
I) LINHA – Espessura
Linha grossa
Linha média (metade da anterior)
Linha fina (metade da anterior)
II) LINHA – Tipos
A- Linhas gerais
B- Linhas principais
C- Linhas auxiliares ( cota , ladrilhos , etc. )
D- Partes invisíveis
_______________________________
E- Eixos de simetria
F- Seções
G- Interrupções
Exercícios
a) Sejam L1, L2 e L3 os lados dados, construir um triângulo sabendo-se que
L1 = 3,5 cm, L2 = 3,8 cm e L3 = 5,5 cm. Considere L3 como sendo a base do triângulo.
b) Sejam L1 e L2 os lados dados, construir um triângulo sabendo-se que
L1 = 4,5 cm, L2 = 5,3 cm e o ângulo central (α) = 30°. Considere L2 como sendo a base do
triângulo.
c) a) Sejam L1 e L2 os lados dados, construir um triângulo sabendo-se que L1 = 5,3 cm,
L2 = 4,4 cm e a altura (H) = 2,5 cm. Considere L1 como sendo a base do triângulo.
d) Sejam a e b os lados dados, construir um retângulo sabendo-se que a = 4,1 cm e b = 2,0
cm. Considere a como sendo a base do retângulo.
e) Seja L1 o lado dado, construir um losango sabendo-se que L1 = 5,0 cm e o ângulo central
é igual a 60°.
f) Sejam A, B, C e D os vértices de um trapézio. Construí–lo sabendo-se que as distâncias
AB = 5,0 cm, BC = 2,5 cm, CD = 3,0 cm e H (altura) = 2,0 cm. Considere AB como sendo a
base do retângulo.
8) ESCALAS E COTAS
8.1) Escalas
O desenho de um objeto, em geral, não pode ser executado em tamanho natural; em
muitos casos o objeto é grande ou pequeno demais. A escala permite aumentar, diminuir ou
manter o tamanho do objeto no desenho de acordo com a situação.
A escala é uma forma de representação que mantém as proporções das medidas
lineares do objeto representado. Ou seja, a escala nada mais é do que uma razão de
proporção entre as medidas no desenho e as medidas reais do objeto.
6
Expressão Gráfica
UFES / CEUNES
Normalmente é empregada a seguinte notação para a representação de escala (E):
E=
1 d
=
M D
em que:
M = denominador da escala;
d = distância no desenho; e
D = distância no terreno.
Por exemplo, se uma feição é representada no desenho com 1 cm de comprimento e
sabe-se que seu comprimento no terreno é de 100 metros, então a escala de representação
utilizada é de 1:10.000. Ao utilizar a equação anterior para o cálculo da escala deve-se ter o
cuidado de transformar as distâncias para a mesma unidade. Por exemplo:
E=
d = 5 cm
5 cm
5 cm
1
=
=
0,5 km 50.000 cm 10.000
D = 0,5 km
As escalas podem ser de redução (1:x), ampliação (x:1) ou naturais (1:1).
Uma escala é dita grande quando apresenta o denominador pequeno (por exemplo,
1:100, 1:200, 1:50, etc.). Já uma escala pequena possui o denominador grande (1:10.000,
1:500.000, etc.).
O valor da escala é adimensional, ou seja, não tem dimensão (unidade). Escrever 1:200
significa que uma unidade no desenho equivale a 200 unidades no terreno. Assim, 1 cm no
desenho corresponde a 200 cm no terreno ou 1 milímetro do desenho corresponde a 200
milímetros no terreno. Como as medidas no desenho são realizadas com uma régua, é
comum estabelecer esta relação em centímetros. Ex.: 1 cm no desenho = 200 cm no terreno.
É comum medir-se uma área em um desenho e calcular-se sua correspondente no
terreno. Isto pode ser feito da seguinte forma: imagina-se um desenho na escala 1:50.
Utilizando esta escala faz-se um desenho de um quadrado de 2 x 2 unidades (u), não
interessa qual é esta unidade. A figura seguinte apresenta este desenho.
A área do quarado no desenho (Ad) será:
2u
Ad = 2u . 2u
2u
Ad = 4u2
7
Expressão Gráfica
UFES / CEUNES
A área do quadrado no terreno (At) será então:
At = (50 . 2u) . (50 . 2u)
At = (2 . 2) . (50 . 50) . (u . u)
At = 4u2 . 502
Substituindo a equação Ad na equação At, e lembrando que M = 50 é o denominador da
escala, a área do terreno, em função da área medida no desenho e da escala é dada pela
equação:
At = Ad . M2
Principais escalas e suas aplicações:
Recomendação da ABNT (1999): NBR 8196 - Desenho técnico - Emprego de escalas
Redução
Natural
1:2
1:5
1:10
Ampliação
2:1
1:1
5:1
10:1
As escalas desta tabela podem ser reduzidas ou ampliadas à razão de 10.
A seguir encontra-se uma tabela com as principais escalas utilizadas e as suas
respectivas aplicações.
Aplicação
Detalhes de terrenos urbanos
Escala
1:50
1:100
Plantas de pequenos lotes e edifícios
1:200
1:500
Plantas de arruamentos e loteamentos urbanos
1:1.000
1:1.000
Plantas de propriedade rurais
1:2.000
1:5.000
1:5.000
Plantas cadastrais de cidades e grandes
1:10.000
propriedades rurais ou industriais
1:20.000
1:50.000
Cartas de municípios
1:100.000
1:200.000 a
Mapas de estados, países, continentes, etc.
1:10.000.000
A escala a ser escolhida para um desenho depende da complexidade do objeto a ser
representado e da finalidade da representação. Em todos os casos, a escala selecionada
deve ser suficiente para permitir uma interpretação fácil e clara da informação
8
Expressão Gráfica
UFES / CEUNES
representada. A escala e o tamanho do objeto em questão são parâmetros para a escolha do
formato da folha de desenho.
Para se decidir sobre a escala ideal, deve-se considerar:
• O tamanho do objeto a ser representado;
• As dimensões do papel; e
• A clareza do desenho a ser realizado.
Ao se executar um desenho, a escala utilizada deverá ser sempre indicada na legenda,
no espaço destinado para tal.
Os ângulos não sofrem redução ou ampliação em sua abertura, independentemente da
escala utilizada no desenho.
Exercícios
1) Qual das escalas é maior 1:1.000.000 ou 1:1.000?
2) Qual das escalas é menor 1:10 ou 1:1.000?
3) Determinar o comprimento de um rio (em km), sendo a escala do desenho de 1:18.000 e
o rio representado no desenho por uma linha com 17,5 cm de comprimento.
4) Determinar qual a escala de uma carta, sabendo-se que distâncias homólogas na carta e
no terreno são, respectivamente, 225 mm e 4,5 km.
5) Com qual comprimento uma estrada de 2500 m será representada na escala 1:10.000?
6) Calcular o comprimento no desenho de uma rua com 30 metros de comprimento nas
escalas abaixo:
Escala Comprimento?
1:100
1:200
1:250
1:500
1:1.000
7) Um lote urbano tem a forma de um retângulo, sendo que o seu comprimento é duas
vezes maior que a sua altura e sua área é de 16.722,54 m2. Calcular os comprimentos dos
lados no desenho se esta área fosse representada na escala 1:10.560.
8) As dimensões de um terreno foram medidas em uma carta e os valores obtidos foram:
250 mm de comprimento por 175 mm de largura. Sabendo-se que a escala do desenho é de
1:2.000, qual é a área do terreno em m2 ?
9) Se a avaliação de uma área resultou em 2.575 cm2 para uma escala de 1:500, a quantos
metros quadrados corresponderá a área no terreno?
9
Expressão Gráfica
UFES / CEUNES
10) Para desenhar um objeto que tem 105 cm em uma folha A4 que tem 210 mm de
largura, qual é a maior escala que pode ser utilizada? Obs.: considerar margem esquerda de
25 mm e direita de 7 mm; caso a escala calculada não seja um valor inteiro, deve-se
arredondar o número obtendo-se uma escala menor inteira.
11) É necessário desenhar um galpão com dimensões de 60 x 15 m em uma folha A3 (420 x
297mm) na escala 1:150. Para que a planta fique centralizada no papel, qual deve ser a
distância (em centímetros) a partir das bordas do papel?
12) Para elaborar a planta de um lote que possui dimensões de 12 x 30 m, qual o menor
formato de papel (série “A”) deverá ser utilizado, na escala 1:50?
Precisão gráfica
Denomina-se de precisão gráfica de uma escala como sendo a menor grandeza passível de
ser representada num desenho, através desta escala.
Erro de grafismo: é erro máximo admissível na elaboração de desenho topográfico para
lançamento de pontos e traçados de linhas, com o valor de 0,2 mm, que equivale a duas
vezes a acuidade visual humana (ABNT NBR 13.133 - Execução de levantamentos
topográficos). E uma função da acuidade visual, habilidade manual e qualidade do
equipamento de desenho.
Exemplo: escala 1:1.000
1
0,2 mm
=
1000
D
D = 20 cm (precisão gráfica)
Assim, pode-se concluir que as dimensões reais do objeto a ser representado que tiverem
valores menores que o erro de grafismo, não terão representação gráfica; portanto, não
aparecerão no desenho. Logo, nas escalas 1:500, 1:2000 e 1:5.000 não se representam os
detalhes de dimensões inferiores a 10 cm, 40 cm e 100 cm, respectivamente.
Em casos onde é necessário representar elementos com dimensões menores que as
estabelecidas pela precisão da gráfica, podem ser utilizados símbolos.
Escala gráfica
A escala gráfica é a representação gráfica de uma escala nominal ou numérica.
Esta forma de representação da escala é utilizada, principalmente, para fins de
acompanhamento de ampliações ou reduções de plantas ou cartas topográficas, em
processos reprodução comuns, cujos produtos finais não correspondem à escala nominal
neles registrada.
A escala gráfica é também utilizada no acompanhamento da dilatação ou retração do papel
no qual o desenho da planta ou carta foi realizado. Esta dilatação ou retração se deve,
normalmente, a alterações ambientais ou climáticas do tipo: variações de temperatura,
variações de umidade, manuseio, armazenamento, etc.
A escala gráfica fornece, rapidamente e sem cálculos, o valor real das medidas executadas
sobre o desenho, mesmo após uma redução ou ampliação do mesmo.
10
Expressão Gráfica
UFES / CEUNES
Exemplo: supondo que a escala de uma planta seja 1:100 e que o intervalo de
representação seja de 1m, a escala gráfica correspondente terá o seguinte aspecto:
A figura a seguir mostra outros tipos de representação da escala gráfica.
Quando utilizada, é obrigatória a indicação da unidade na escala gráfica.
8.2) Cotagem ou Dimensionamento
A norma técnica NBR 10126 (1987) fixa os princípios gerais de cotagem a serem
aplicados em desenhos técnicos.
O desenho técnico, além de representar a forma tridimensional, dentro de uma escala,
deve conter informações sobre as dimensões do objeto representado. As dimensões irão
definir as características geométricas do objeto, dando valores de tamanho e posição aos
diâmetros, aos comprimentos, aos ângulos e a todos os outros detalhes que compõem sua
forma espacial.
Trata-se de indicar no desenho as dimensões do objeto representado. Para isso são
utilizadas as cotas, ou seja, números que correspondem às medidas dos objetos. As cotas
são constituídas pela linha de cota ou de medida, linha de chamada, setas e pelo valor
numérico expresso em uma determinada unidade de medida. As setas indicam o limite da
linha de cota e o valor da cota indica o tamanho real do objeto.
As cotas devem ser distribuídas pelas vistas e dar todas as dimensões necessárias para
viabilizar a construção do objeto desenhado, com o cuidado de não colocar cotas
desnecessárias. No caso das vistas, uma determinada dimensão que é representada, por
exemplo, na vista frontal e superior só precisa ser indicada em uma delas.
Uma demonstração da utilização de cotas está representada na figura seguinte:
11
Expressão Gráfica
UFES / CEUNES
Figura 6 – Representação de um desenho por meio de cotas.
Regras para o emprego de cotas
As cotas devem ser escritas acompanhando a direção das linhas de cota e devem
representar a medida real do objeto, independente da escala utilizada. Deve-se evitar o
cruzamento das linhas de cota. As linhas de cota podem ser contínuas ou interrompidas.
Quando se utilizam as linhas de cota contínuas, o valor da cota deve ser escrito acima das
linhas de cota horizontais e à esquerda das linhas de cota verticais. Quando se utilizam
linhas de cotas interrompidas o valor deve ser escrito no intervalo da interrupção, sem
rotação. A Figura 7 (a) mostra que tanto as linhas auxiliares (linhas de chamada), como as
linhas de cota, são linhas contínuas e finas. As linhas de chamadas devem ultrapassar
levemente as linhas de cota e também deve haver um pequeno espaço entre a linha do
elemento dimensionado e a linha de chamada.
Figura 7 – Forma para apresentação das cotas.
As linhas de centro ou as linhas de contorno podem ser usadas como linhas de
chamada, conforme mostra a Figura 7 (b). No entanto, é preciso destacar que as linhas de
centro ou as linhas de contorno não devem ser usadas como linhas de cota.
As linhas de chamada devem ser preferencialmente perpendiculares ao ponto cotado.
Em alguns casos, para melhorar a clareza da cotagem, as linhas de chamada podem ser
12
Expressão Gráfica
UFES / CEUNES
oblíquas em relação ao elemento dimensionado, porém mantendo o paralelismo entre si,
conforme mostra a Figura 7 (c).
O limite da linha de cota pode ser indicado por setas, que podem ser preenchidas ou
não, ou por traços inclinados, conforme mostra a Figura 8 (a). A maioria dos tipos de
desenho técnico utiliza as setas preenchidas. Os traços inclinados são mais utilizados nos
desenhos arquitetônicos. Em um mesmo desenho a indicação dos limites da cota deve ser
de um único tipo e também deve ser de um único tamanho. Só é permitido utilizar outro
tipo de indicação de limites da cota em espaços muito pequenos, conforme mostra a Figura
8 (b).
(a)
(b)
Figura 8 – Limite (a) e indicação (b) da linha de cota.
No dimensionamento deve-se observar ainda:
• as linhas de cota devem ser colocadas preferencialmente fora da figura;
• deve-se evitar a repetição de cotas;
• deve-se deixar um pequeno espaço entre a figura e a linha de chamada;
• as cotas de um desenho ou projeto devem ser expressas em uma única unidade;
• uma cota não deve ser cruzada por uma linha do desenho;
• as linhas de cota são desenhadas paralelas à direção da medida;
• a altura dos algarismos deve ser uniforme dentro de um mesmo desenho.
9) VISTAS E PROJEÇÕES
9.1) Sistemas de projeções
Projeção é a operação pela qual um ponto, uma linha ou um objeto tridimensional é
projetado em um plano através de linhas denominadas de projetantes. Este plano é
denominado de plano de projeção.
Plano de projeção é a superfície onde se projeta o modelo. A tela de cinema é um bom
exemplo de plano de projeção.
As projeções poderão ser do tipo (Figura 9):
1 - Centrais ou Cônicas: quando as linhas projetantes convergem para um ponto;
2 – Cilíndricas ou Paralelas: quando as linhas projetantes são paralelas entre si. Estas ainda
poderão ser ortogonais, quando as projetantes são perpendiculares ao plano de projeção
ou oblíquas, quando as projetantes são oblíquas ao referido plano.
13
Expressão Gráfica
UFES / CEUNES
Figura 9 – Tipos de projeções: (A) centrais e (B) paralelas.
Projeções cônicas
O centro das projeções é a origem das linhas projetantes, localizado a uma distância
finita do plano de projeção.
Figura 10 - Sistema de projeções cônicas
Projeções cilíndricas oblíquas
O centro de projeção se localiza a uma distância infinita do plano de projeção. Dessa
forma, as linhas projetantes têm uma única direção e, nesse caso específico, a direção é
oblíqua ao plano de projeção e o ângulo de incidência é variável, sendo diferente de 0, 90 e
180 graus.
14
Expressão Gráfica
UFES / CEUNES
Figura 11 - Sistema de projeções cilíndricas oblíquas
Projeções cilíndricas ortogonais
O centro de projeções se localiza a uma distância infinita do plano de projeções e a
direção das projetantes é ortogonal ao plano de projeção. O ângulo de incidência é igual a
90 graus. É o sistema utilizado na geometria descritiva – base para representação no
desenho técnico.
Figura 12 - Sistema de projeções cilíndricas ortogonais
Os planos de projeção podem ocupar várias posições no espaço. Em desenho técnico
usam-se dois planos básicos para representar as projeções de modelos: um plano
horizontal e um plano vertical, que se cortam perpendicularmente.
Esses dois planos, perpendiculares entre si, dividem o espaço em quatro regiões
chamadas diedros.
15
Expressão Gráfica
UFES / CEUNES
O plano horizontal pode ser dividido em:
SPHA: semiplano horizontal anterior
SPHP: semiplano horizontal posterior
O plano vertical pode ser dividido em:
SPVS: semiplano vertical superior
SPVI: semiplano vertical inferior
O método de representação de objetos em dois semiplanos perpendiculares entre si,
criado por Gaspar Monge, é também conhecido como método mongeano. Atualmente, a
maioria dos países que utiliza o método mongeano adota a projeção ortográfica no 1º
diedro. No Brasil, a ABNT recomenda a representação no 1º diedro.
Entretanto, alguns países, como os Estados Unidos e o Canadá, representam seus desenhos
técnicos no 3º diedro.
Ao ler e interpretar desenhos técnicos, o primeiro cuidado que se deve ter é identificar
em qual diedro está representado o modelo. Essa verificação é importante para se evitar o
risco de interpretar erradamente as características do objeto.
No Brasil, onde se adota a representação no 1º diedro, além do plano vertical e do plano
horizontal, utiliza-se um terceiro plano de projeção: o plano lateral. Este plano é
perpendicular ao plano vertical e ao plano horizontal.
Plano vertical
Plano lateral
Plano horizontal
A vista representa a peça sendo observada de uma determinada posição. Ou seja, nas
projeções ortogonais, apesar de estarmos vendo desenhos planos (bidimensionais), em
cada vista há uma profundidade, não visível, que determina a forma tridimensional da peça
representada.
A projeção do modelo no plano vertical dá origem à vista frontal;
A projeção do modelo no plano horizontal dá origem à vista superior;
A projeção do modelo no plano lateral dá origem à vista lateral esquerda.
16
Expressão Gráfica
UFES / CEUNES
Imagine agora que o modelo tenha sido retirado e veja como ficam apenas as suas
projeções nos três planos:
Mas, em desenho técnico, as vistas devem ser mostradas em um único plano. Para tanto,
usa-se um recurso que consiste no rebatimento dos planos de projeção horizontal e lateral.
Veja como isso é feito no 1º diedro:
17
Expressão Gráfica
UFES / CEUNES
Além destas três vistas, ainda existem a vista lateral direita, a vista inferior e a vista
posterior. Vide norma ABNT NBR 10067.
Dificilmente será necessário fazer seis vistas para representar qualquer objeto. Porém,
quaisquer que sejam as vistas utilizadas, as suas posições relativas obedecerão às
disposições definidas pelas vistas principais. Na maioria dos casos, o conjunto formado
pelas vistas de frente, vista superior e uma das vistas laterais é suficiente para representar,
com perfeição, o objeto desenhado.
As posições relativas das vistas, no 1º diedro, não mudam: a vista frontal, que é a vista
principal da peça, determina as posições das demais vistas; a vista superior aparece
sempre representada abaixo da vista frontal; a vista lateral esquerda aparece sempre
representada à direita da vista frontal.
O ponto de partida para determinar as vistas necessárias é escolher o lado do desenho
que será considerado como frente. Normalmente, considerando a peça em sua posição de
trabalho ou de equilíbrio, toma-se como frente o lado que melhor define a forma do
desenho. Quando dois lados definem bem a forma do desenho, escolhe-se o de maior
comprimento. Feita a vista de frente faz-se tantos rebatimentos quantos forem necessários
para definir a forma do desenho.
10)
PERSPECTIVAS
É uma forma de representação gráfica que demonstra as três dimensões de um objeto
em um único plano, gerando idéia de profundidade e relevo.
Existem diferentes tipos de perspectiva, sendo que as mais comuns são:
- Perspectiva Isométrica;
- Perspectiva Cavaleira; e
- Perspectiva Bimétrica.
Perspectiva é a representação de objetos como são vistos na realidade, de acordo com
sua posição, forma e tamanho. A perspectiva permite também a visualização do
comprimento, da altura e da largura do objeto.
18
Expressão Gráfica
UFES / CEUNES
Em perspectiva, o objeto é representado sobre uma superfície plana, entretanto, os
procedimentos utilizados permitem que a representação aproxime-se da imagem real.
A perspectiva denominada axonométrica é uma projeção cilíndrica ortogonal sobre um
plano oblíquo em relação às três dimensões do corpo a representar (eixos X, Y e Z).
Existem diversas inclinações possíveis do objeto, podendo-se concluir que existem
infinitas perspectivas que podem ser obtidas por este processo. Dessa forma, a perspectiva
axonométrica pode ser classificada de acordo com os ângulos formados pelos eixos
principais, podendo ser isométrica ou bimétrica. A perspectiva isométrica é a mais utilizada
em desenhos técnicos.
Exemplos:
a) Perspectivas Cavaleiras a 30°, a 45° e a 60°
b) Perspectivas Isométrica e Bimétrica
Perspectiva
Largura
Altura
Profundidade
Relação das medidas reais com as do desenho
Cavaleira
Isométrica
o
30
45o
60o
1:1
1:1
1:1
1:4/5
1:1
1:1
1:1
1:4/5
1:2/3
1:1/2
1:1/3
1:4/5
Bimétrica
1:1
1:1
1:1/2
19
Expressão Gráfica
UFES / CEUNES
Exercícios
1) Desenhar um cubo com 6 cm de aresta, escala 1:1, nas perspectivas listadas no quadro
anterior.
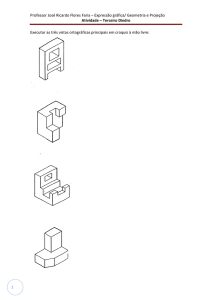
2) Representar a perspectiva do objeto na escala de 1:50 representado nas vistas abaixo. As
dimensões são representadas em milímetros.
Repostas dos exercícios sobre escala:
01) a escala 1:1.000 é maior;
02) a escala 1:1.000 é menor;
03) 3,15 km; 4) 1:20.000;
05) 25 cm;
06) 30 cm, 15 cm, 12 cm, 6 cm, 3 cm;
07) 0,866 x 1,732 cm;
08) 175.000 m2;
09) 64.375 m2;
10) 1:6;
11) 1 cm na dimensão de 420 mm e 9,85 na dimensão de 297 mm;
12) formato A1.
20