Exercícios – Leis de Kirchhoff

Eletricidade Aplicada
Exercícios - Leis de Kirchhoff.odt
Resolução de circuitos usando lei de Kirchhoff
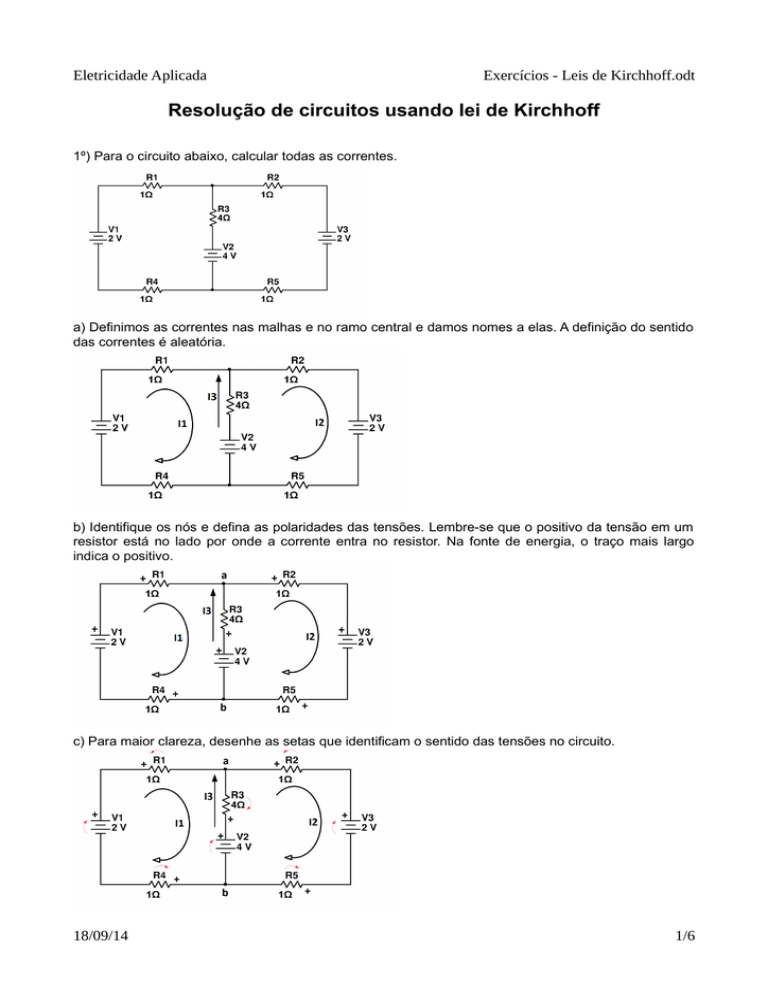
1º) Para o circuito abaixo, calcular todas as correntes.
a) Definimos as correntes nas malhas e no ramo central e damos nomes a elas. A definição do sentido
das correntes é aleatória.
b) Identifique os nós e defina as polaridades das tensões. Lembre-se que o positivo da tensão em um
resistor está no lado por onde a corrente entra no resistor. Na fonte de energia, o traço mais largo
indica o positivo.
c) Para maior clareza, desenhe as setas que identificam o sentido das tensões no circuito.
18/09/14
1/6
Eletricidade Aplicada
Exercícios - Leis de Kirchhoff.odt
d) O circuito está pronto para análise. Vamos analisar primeiramente o nó (a). Aplicando a 1ª lei de
Kirchhoff, ΣI = 0, temos:
I1 + I3 = I2 (1) (I1 e I3 chegam ao nó, I2 sai do nó)
e) Analisemos agora a malha 1, definida pela corrente I1, aplicando a 2ª lei de Kirchhoff, ΣV = 0. As
tensões sobre os resistores serão indicadas pela letra V seguido pelo nome do resistor, por exemplo, a
tensão sobre o resistor R1 é VR1, sobre R2 é VR2 e assim suscetivamente. Tensões com o mesmo
sentido da corrente da malha são positivas e tensões com sentido diferente são negativas.
V1 – VR1 + VR3 – V2 – VR4 = 0
Substituindo as tensões das fontes pelos seus valores e as tensões dos resistores pelo produto R*I,
temos então:
2 – 1•I1 + 4•I3 – 4 – 1•I1 = 0 (2)
f) Analisando a malha 2, pela segunda lei de Kirchhoff, temos:
V2 – VR3 – VR2 – V3 – VR5 = 0
Substituindo as tensões das fontes pelos seus valores e as tensões dos resistores pelo produto R*I,
temos então:
4 – 4•I3 – 1•I2 – 2 – 1•I2 = 0 (3)
g) Temos então as seguintes equações para o circuito:
I1 + I3 = I2
2 – 1•I1 + 4•I3 – 4 – 1•I1 = 0
4 – 4•I3 – 1•I2 – 2 – 1•I2 = 0
(1)
(2)
(3)
h) Agrupando os termos comuns nas equações (2) e (3):
– 2 – 2•I1 + 4•I3 = 0
2 – 4•I3 – 2•I2 = 0
(2)
(3)
i) Substituindo I2 de (1) em (3):
2 – 4•I3 – 2•(I1 + I3) = 0 ==> 2 – 4•I3 – 2•I1 – 2•I3 = 0 ==> 2 – 6•I3 – 2•I1 = 0 (4)
j) Isolando I1 de (2) e (4) e igualando os resultados:
– 2 – 2⋅I1+ 4⋅I3=0 ⇒−2⋅I1=2−4⋅I3⇒ 2⋅I1=4⋅I 3−2⇒I1=
2 – 6⋅I 3 – 2⋅I 1=0⇒ – 2⋅I 1=6⋅I 3 – 2⇒ 2⋅I 1=2 – 6⋅I 3 ⇒I1=
4⋅I 3−2
⇒I1=2⋅I3−1 (5)
2
2−6⋅I 3
⇒I 1=1−3⋅I 3
2
2
2⋅I3−1=1−3⋅I3 ⇒ 2⋅I3+3⋅I3=1+1 ⇒5⋅I 3=2 ⇒I3= ⇒ I3=0,4 A
5
k) Substituindo I3 em (5):
18/09/14
2/6
Eletricidade Aplicada
Exercícios - Leis de Kirchhoff.odt
I1=2⋅I 3−1⇒ I1=2⋅0,4−1⇒ I1=0,8−1⇒ I1=−0,2 A
l) Calculando I2:
I2=I1+I3 ⇒I 2=−0,2+0,4 ⇒I2=0,2 A
m) Resposta: I1 = -0,2A, I2 = 0,2A e I3 = 0,4A.
2º) Determine a tensão em R6 no circuito abaixo.
a) Analisando o circuito ao lado, temos
que determinar a corrente que circula
por R6 para determinarmos sua tensão.
Percebemos
também
que
para
determinarmos IR6, teremos que
analisar o circuito por Kirchhoff, pois não
há
associações
possíveis
para
reduzirmos o circuito.
b) Definimos as correntes nas malhas e no ramo central e damos nomes a elas. A definição do sentido
das correntes é aleatória.
c) Identifique os nós e defina as polaridades das tensões. Lembre-se que o positivo da tensão em um
resistor está no lado por onde a corrente entra no resistor. Na fonte de energia, o traço mais largo
indica o positivo. Para maior clareza, desenhe as setas que identificam o sentido das tensões no
circuito.
18/09/14
3/6
Eletricidade Aplicada
Exercícios - Leis de Kirchhoff.odt
d) Analisemos agora o nó (a) e as malhas 1 e 2.
Do nó (a):
I3 + I1 = I2
(Equação 1)
Da malha 1:
V1 – VR1 – V2 + VR3 – VR6 – VR4 = 0
(Equação 2)
Da malha 2:
V2 – VR2 – V3 – VR5 – VR3 = 0
(Equação 3)
e) Substituindo as tensões das fontes pelos seus valores e as tensões dos resistores pelo produto R•I
na equação 2, temos:
50−30⋅I1−150+5⋅I 3−2⋅I1−3⋅I1=0 ⇒−100−35⋅I1+5⋅I3=0
(4)
Fazendo o mesmo para a equação 2:
150−10⋅I2−40−10⋅I 2−5⋅I3=0⇒ 110−20⋅I2−5⋅I 3=0
(5)
f) Portanto ficamos com as seguintes equações para solução do problema:
I3 + I1 = I2
– 100 – 35•I1 + 5•I3 = 0
110 – 20•I2 – 5•I3 = 0
(1)
(4)
(5)
g) Para calcular VR6 temos que determinar I1. Para tanto, substituiremos (1) em (5) e isolaremos I3
em (4) e (5).
110−20⋅I2−5⋅I3=0⇒110−20⋅(I1+I 3)−5⋅I3=0 ⇒110−20⋅I1−20⋅I3−5⋅I3=0 ⇒
– 25⋅I 3=– 110+ 20⋅I1⇒ I3=
110 – 20⋅I1
25
– 100 – 35⋅I1+5⋅I3=0⇒ 5⋅I3=35⋅I1+100⇒ I3=
(6) ==> de (5)
35⋅I1+100
5
(7) ==> de (4)
h) Igualando (6) e (7):
110 – 20⋅I1 35⋅I1+ 100 110 – 20⋅I1
=
⇒
=35⋅I1+100⇒ 110 – 20⋅I1=175⋅I1+ 500⇒
25
5
5
195⋅I1=– 390⇒ I1=
– 390
⇒I1=– 2 A
195
i) VR6 = R6•I1. Portanto, VR6 = -4 Volts
j) Resposta: A tensão sobre VR6 é de -4 Volts. Isso indica que a polaridade de VR6 é inversa a
definida no circuito.
18/09/14
4/6
Eletricidade Aplicada
Exercícios - Leis de Kirchhoff.odt
3º) No circuito abaixo, as correntes têm os sentidos indicados. Se a intensidade da corrente I3 é 5A,
então o valor da resistência do resistor R é:
Para determinarmos o valor de R,
precisamos achar a tensão sobre R (VR)
e a corrente I1. Como o circuito não
permite associações de resistores para
simplificação, temos que aplicar as leis
de Kirchhoff para solução do problema.
Como o sentido das correntes já está
definido, vamos polarizar as tensões e
definir os nós.
a) Aplicando a 1ª lei de Kirchhoff no nó
(a), temos:
I1 = I2 + I3
(1)
b) Aplicando a 2ª lei de Kirchhoff na
malha 1, temos (o sentido da corrente é
horário, definido na descrição do
problema):
V1 – VR1 – VR = 0
(2)
c) Idem para malha 2, temos:
VR1 – V3 – VR2 = 0
(3)
d) Substituindo os valores fornecidos pelo problema, teremos:
(1)
(2)
(3)
I1 = I2 + 5
V1 – R1•I3 – R•I1 = 0 ==> 60 – 4•5 – R•I1 = 0
VR1 – V3 – VR2 = 0 ==> 4•5 – 14 – 2•I2 = 0
e) De (1) temos:
I1 = I2 + 5 ==> I2 = I1 – 5
(4)
f) Substituindo (4) em (3) e isolando I1:
4•5 – 14 – 2(I1 – 5) = 0 ==> 20 – 14 – 2•I1 + 10 = 0 ==> 16 – 2•I1 = 0 ==>
2•I1 = 16 ==> I1 = 16/2 ==>
I1 = 8 A
g) Substituindo I1 em (2) temos:
60 – 4•5 – R•8 = 0 ==> 60 – 20 – 8•R = 0 ==> 8•R = 40 ==> R = 40/8 ==>
R=5Ω
h) Resposta: O valor de R é 5 Ω.
18/09/14
5/6
Eletricidade Aplicada
Exercícios - Leis de Kirchhoff.odt
Exercícios Propostos:
1º) Para o circuito abaixo, calcular todas as correntes.
As correntes devem resultar 17,5A /
11,25A / 6,25A)
2º) Para o circuito abaixo, calcular a tensão sobre R7.
(VR7 = 3 Volts / positivo para cima)
3º) Para o circuito abaixo, determinar V e R, sendo que os sentidos das correntes fornecidas estão
corretos.
(R = 10Ω / V = 52V)
18/09/14
6/6