Eletrotécnica

Eletrotécnica
Energia
Capacidade de realizar trabalho
E=τ ...
τ= F.∆x
Formas de Energia
1-Potencial ou de posição -
Ep=m.g.h
2- Cinética de movimento -
Ec= ½ m.v2
g é a força.
F = m.a
Força Elétrica
Lei de Coulomb
.q
q
F = 4π
εr
1
2
12
2
o
Campo Elétrico
F= q.E
Potencial Elétrico
V= E.dx
Ep= V.q
V.. Volt
Potência Elétrica
E
W =d
dt
p
W = V .d
q
= V .i
dt
q
C=
V
Capacitância
A carga esta contida em um dispositivo.
( Farad)
Energia em um capacitor
E=1/2C.V2
Capacitor de placas paralelas
ε
C=
0
d
A
Capacitor Esférico
ε
C = 4π
0
a.b
b−a
Associação de Capacitores
a) Paralelo
n
C =∑C
eq
i=1
i
b) serie
1= 1
∑
c C
n
eq
i=1
i
Eletroquímica Corrente Resistência e Resistividade
A pilha de Volta (Alessandro ) permitiu utilização de correntes
maiores e contínuas
Condutores – metais – soluções iônicas
Isolantes - não metais
Lei de Ohm
V = R.i
Para condutores cilíndricos ou
prismas
l
R=ρ
A
Circuitos Elétricos
Associação de Resistores
a) Série
n
r = ∑r
eq
i=1
i
b) Paralelo
1= 1
∑
r
r
n
eq
i=1
i
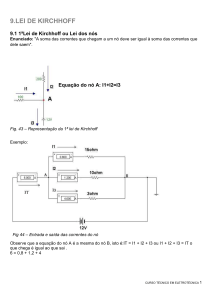
Leis de Kirchhoff
As leis de Kirchhoff (definidas pelo físico alemão Gustav Kirchhoff) servem para ditar o
comportamento das grandezas em um circuito elétrico composto por diferentes laços e nós.
Laço: caminho fechado em um circuito elétrico Nó: ponto de conexão de dois ou mais
componentes em um circuito.
Não e um nó
1a. Lei de Kirchhoff
A soma algébrica das correntes presentes em cada nó é igual a zero.
n
i =∑i =0
j
k=1
k
onde ik representa a corrente em cada um dos n ramos de um dado nó j
2a. Lei de Kirchhoff
A soma algébrica das tensões ao longo de qualquer laço é igual a zero
n
∑v =0
k=1
k
onde vk representa a tensão registrada em cada componente do laço.
Associação de Resistores
c) Série
n
r = ∑r
eq
i=1
i
d) Paralelo
1= 1
∑
r
r
n
eq
i=1
i
Solução dos circuitos
a) Redução a equivalentes
B) Métodos dos Nós
Dado um nó “j” ligado a “n” nós.
Separando do somatória as correntes “Injetadas” das corrente de ramo,
I =∑ i
(1)
Onde Ii corrente injetada pelas fontes e ijk é a corrente no ramo jk,
j
jk
1
ijk = (Vj −Vk ) rjk
(2)
Substituindo 2 em 1 e re-arrumando
I = G *V
Onde:
G
i
=
e uma matriz elementos gii ∑rik
1
=−
e gij rik
Método das malhas
n
∑v =0 v = R .I
k=1
k
1
1 1,
v2 = R2.I2
v3 = R3.(I1-I2)
substituindo e re-arrumando
e = R *I
Onde
R
é uma matriz de elementos
r = ∑R e r = −R
ii
I
ij
IJ