Pré-Cálculo

Pré-Cálculo
Humberto José Bortolossi
Departamento de Matemática Aplicada
Universidade Federal Fluminense
Aula 16
23 de junho de 2011
Aula 16
Pré-Cálculo
1
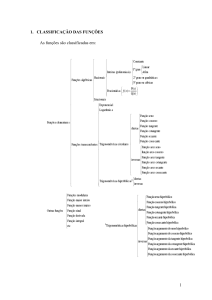
Função polinomial
Aula 16
Pré-Cálculo
2
Função polinomial
Definição
Diz-se que p : R → R é uma função polinomial se existe inteiro n ≥ 0
e existem números reais a0 , a1 , . . . , an tais que, para todo x ∈ R,
tem-se
p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 .
Se an 6= 0, dizemos que p tem grau n.
Uma função polinomial chama-se identicamente nula quando se tem
p(x) = 0 para todo x ∈ R (não se define grau para uma função
polinomial identicamente nula).
Dizemos que α é uma raiz de p se p(α) = 0 (note que todo número
real é raiz de uma função polinomial identicamente nula).
Aula 16
Pré-Cálculo
3
Função polinomial
Definição
Diz-se que p : R → R é uma função polinomial se existe inteiro n ≥ 0
e existem números reais a0 , a1 , . . . , an tais que, para todo x ∈ R,
tem-se
p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 .
Se an 6= 0, dizemos que p tem grau n.
Uma função polinomial chama-se identicamente nula quando se tem
p(x) = 0 para todo x ∈ R (não se define grau para uma função
polinomial identicamente nula).
Dizemos que α é uma raiz de p se p(α) = 0 (note que todo número
real é raiz de uma função polinomial identicamente nula).
Aula 16
Pré-Cálculo
4
Função polinomial
Definição
Diz-se que p : R → R é uma função polinomial se existe inteiro n ≥ 0
e existem números reais a0 , a1 , . . . , an tais que, para todo x ∈ R,
tem-se
p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 .
Se an 6= 0, dizemos que p tem grau n.
Uma função polinomial chama-se identicamente nula quando se tem
p(x) = 0 para todo x ∈ R (não se define grau para uma função
polinomial identicamente nula).
Dizemos que α é uma raiz de p se p(α) = 0 (note que todo número
real é raiz de uma função polinomial identicamente nula).
Aula 16
Pré-Cálculo
5
Função polinomial
Definição
Diz-se que p : R → R é uma função polinomial se existe inteiro n ≥ 0
e existem números reais a0 , a1 , . . . , an tais que, para todo x ∈ R,
tem-se
p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 .
Se an 6= 0, dizemos que p tem grau n.
Uma função polinomial chama-se identicamente nula quando se tem
p(x) = 0 para todo x ∈ R (não se define grau para uma função
polinomial identicamente nula).
Dizemos que α é uma raiz de p se p(α) = 0 (note que todo número
real é raiz de uma função polinomial identicamente nula).
Aula 16
Pré-Cálculo
6
Função polinomial
Definição
Diz-se que p : R → R é uma função polinomial se existe inteiro n ≥ 0
e existem números reais a0 , a1 , . . . , an tais que, para todo x ∈ R,
tem-se
p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 .
Se an 6= 0, dizemos que p tem grau n.
Uma função polinomial chama-se identicamente nula quando se tem
p(x) = 0 para todo x ∈ R (não se define grau para uma função
polinomial identicamente nula).
Dizemos que α é uma raiz de p se p(α) = 0 (note que todo número
real é raiz de uma função polinomial identicamente nula).
Aula 16
Pré-Cálculo
7
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
8
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
9
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
10
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
11
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
12
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
13
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
14
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
15
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
16
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
17
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
18
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
19
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
20
Função polinomial: exemplos
São exemplos de funções polinomiais:
p(x) = x 3 − 2 x + 1 (de grau 3),
p(x) = x 7 −
√
2 x − 9 (de grau 7),
as funções afins e quadráticas,
q
p(x) = (x 2 + 1)2 = x 2 + 1, p(x) = sec2 (arctg(x)) = x 2 + 1.
Não são funções polinomiais:
f (x) =
Aula 16
1
= x −1 ,
x
f (x) =
√
x = x 1/2 ,
f (x) = 2x .
Pré-Cálculo
21
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
22
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
23
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
24
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
25
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
26
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
27
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
28
Função polinomial versus polinômio
Um polinômio é uma expressão formal do tipo
p(X ) = an X n + an−1 X n−1 + · · · + a1 X + a0 ,
onde a0 , a1 , . . . , an são números (os coeficientes do polinômio) e X é um
símbolo (chamado indeterminada), sendo X i uma abreviatura para X · X · · · · · X
(i fatores). Em essência, o polinômio p(X ) é o mesmo que a lista ordenada de seus
coeficientes:
p(X ) = (a0 , a1 , . . . , an ).
Se os coeficientes são números reais, então cada polinômio determina uma função
polinomial e vice-versa. Por esse motivo, para o caso dos números reais, não há
necessidade de fazer distinção entre polinômios e funções polinomiais. Existem
certos conjuntos numéricos, contudo, onde a diferença existe.
Aula 16
Pré-Cálculo
29
O algoritmo da divisão de Euclides
Aula 16
Pré-Cálculo
30
O algoritmo da divisão de Euclides
O algoritmo da divisão de Euclides
Dadas duas funções polinomiais p e d (com d não identicamente
nula), existem únicas funções polinomiais q e r tais que
p(x) = q(x)d(x) + r (x), ∀x ∈ R,
onde r é identicamente nula ou o grau de r é menor do que o grau
de d. Neste caso, p é chamado de dividendo, d de divisor, q de
quociente e r de resto da divisão de p por d. Quando o resto r é uma
função identicamente nula, dizemos que p é divisível por d.
É possível demonstrar este teorema formalizando o processo
que descreveremos a seguir.
Aula 16
Pré-Cálculo
31
O algoritmo da divisão de Euclides
O algoritmo da divisão de Euclides
Dadas duas funções polinomiais p e d (com d não identicamente
nula), existem únicas funções polinomiais q e r tais que
p(x) = q(x)d(x) + r (x), ∀x ∈ R,
onde r é identicamente nula ou o grau de r é menor do que o grau
de d. Neste caso, p é chamado de dividendo, d de divisor, q de
quociente e r de resto da divisão de p por d. Quando o resto r é uma
função identicamente nula, dizemos que p é divisível por d.
É possível demonstrar este teorema formalizando o processo
que descreveremos a seguir.
Aula 16
Pré-Cálculo
32
O algoritmo da divisão de Euclides
O algoritmo da divisão de Euclides
Dadas duas funções polinomiais p e d (com d não identicamente
nula), existem únicas funções polinomiais q e r tais que
p(x) = q(x)d(x) + r (x), ∀x ∈ R,
onde r é identicamente nula ou o grau de r é menor do que o grau
de d. Neste caso, p é chamado de dividendo, d de divisor, q de
quociente e r de resto da divisão de p por d. Quando o resto r é uma
função identicamente nula, dizemos que p é divisível por d.
É possível demonstrar este teorema formalizando o processo
que descreveremos a seguir.
Aula 16
Pré-Cálculo
33
O algoritmo da divisão de Euclides
O algoritmo da divisão de Euclides
Dadas duas funções polinomiais p e d (com d não identicamente
nula), existem únicas funções polinomiais q e r tais que
p(x) = q(x)d(x) + r (x), ∀x ∈ R,
onde r é identicamente nula ou o grau de r é menor do que o grau
de d. Neste caso, p é chamado de dividendo, d de divisor, q de
quociente e r de resto da divisão de p por d. Quando o resto r é uma
função identicamente nula, dizemos que p é divisível por d.
É possível demonstrar este teorema formalizando o processo
que descreveremos a seguir.
Aula 16
Pré-Cálculo
34
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
35
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
36
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
37
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
38
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
39
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
40
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
41
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
42
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
43
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
44
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
45
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
46
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
47
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
48
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
49
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
50
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
51
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
52
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
53
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
54
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
55
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
56
O algoritmo da divisão de Euclides: exemplo
3
x| 4 − 3x{z
+ x − 1} = (x 2 + x − 3) (x 2 − x + 1) + (−3x + 2)
{z
}|
{z
} | {z }
|
p(x)
Aula 16
q(x)
d(x)
r (x)
Pré-Cálculo
57
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
58
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
59
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
60
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
61
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
62
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
63
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
64
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
65
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
66
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
67
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
68
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
69
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
70
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
71
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
72
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
73
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
74
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
75
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
76
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
77
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
78
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
79
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
80
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + |{z}
4
|
{z
} | {z }
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
81
O algoritmo da divisão de Euclides: exemplo
x| 4 − 3x 3{z
+ 2x 2 − 2} = (x 3 − 4x 2 + 6x − 6) (x + 1) + 4
|
{z
} | {z } |{z}
p(x)
Aula 16
q(x)
d(x)
Pré-Cálculo
r (x)
82
O dispositivo de Horner
(dispositivo de Briot-Ruffini)
Aula 16
Pré-Cálculo
83
O dispositivo de Horner (dispositivo de Briot-Ruffini)
O dispositivo de Horner (dispositivo de Briot-Ruffini) é uma
maneira rápida de efetuarmos a divisão de uma função
polinomial p por uma função polinomial de grau 1 da forma
d(x) = x − α.
Aula 16
Pré-Cálculo
84
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−3 2
d(x) = x + 1 = x − (−1).
0
−2
−1
Aula 16
Pré-Cálculo
85
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−3 2
d(x) = x + 1 = x − (−1).
0
−2
−1
1
?
Aula 16
Pré-Cálculo
86
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
−3 2
d(x) = x + 1 = x − (−1).
0
−2
−1
*
·(−1)
1
Aula 16
Pré-Cálculo
87
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
0
−2
− 1+
1
Aula 16
−3 2
d(x) = x + 1 = x − (−1).
−4
?
Pré-Cálculo
88
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
0
−2
−1 4
1
Aula 16
−3 2
d(x) = x + 1 = x − (−1).
*
·(−1)
−4
Pré-Cálculo
89
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
−3 2
0
−2
− 1 4+
1
Aula 16
d(x) = x + 1 = x − (−1).
−4 6
?
Pré-Cálculo
90
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
Aula 16
−3 2
−1 4
1
d(x) = x + 1 = x − (−1).
−4 6
0
−2
−6
*
·(−1)
Pré-Cálculo
91
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
1
Aula 16
d(x) = x + 1 = x − (−1).
−3 2
0
−1 4
− 6+
−4 6
−6
−2
?
Pré-Cálculo
92
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
1
Aula 16
d(x) = x + 1 = x − (−1).
−3 2
0
−2
−1 4
−6
6
−4 6
−6
*
·(−1)
Pré-Cálculo
93
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
1
Aula 16
d(x) = x + 1 = x − (−1).
−3 2
0
−2
−1 4
−6
6+
−4 6
−6
4
?
Pré-Cálculo
94
O dispositivo de Horner (dispositivo de Briot-Ruffini)
p(x) = x 4 − 3x 3 + 2x 2 + 0x − 2,
1
−1
1
Aula 16
d(x) = x + 1 = x − (−1).
−3 2
0
−2
−1 4
−6
6
−4 6
−6
4
Pré-Cálculo
95
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
96
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
97
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
98
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
99
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
100
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
101
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
102
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
103
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
104
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
105
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
106
Teorema de D’Lambert
Teorema (de D’Lambert). Se p é uma uma função polinomial e d(x) = x − α, com
α ∈ R, então o resto da divisão de p por d é p(α).
Demonstração. Pelo algoritmo da divisão de Euclides, p(x) = q(x)(x − α) + r (x), onde
r é uma função polinomial identicamente nula ou de grau zero (isto é, r é uma função
constante: r (x) = c, para todo x ∈ R). Logo,
p(α) = q(α)(α − α) + c
⇒
p(α) = c.
⇒
r (x) = c = p(α).
No exemplo anterior, p(x) = x 4 − 3x 3 + 2x 2 − 2, d(x) = x + 1 e r (x) = 4 = p(−1).
Corolário. Uma função polinomial p é divisível por d(x) = x − α, com α ∈ R, se, e
somente se, α é uma raiz de p, isto é, se, e somente se,
p(x) = q(x)(x − α),
para todo x ∈ R, onde q é uma função polinomial de grau n − 1 se p tem grau n.
Aula 16
Pré-Cálculo
107
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
108
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
109
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
110
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
111
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
112
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
113
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
114
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
115
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
116
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
117
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
118
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
119
Teorema de D’Lambert
Corolário. Mais geralmente, α1 , α2 , . . . , αk são raízes distintas de uma função
polinomial p se, e somente se,
p(x) = q(x) (x − α1 )(x − α2 ) · · · (x − αk ),
(∗)
para todo x ∈ R, onde q é uma função polinomial de grau n − k se p tem grau n.
Demonstração. Se α1 é uma raiz de p, então pelo corolário anterior, podemos escrever
que p(x) = q1 (x)(x −α1 ), para todo x ∈ R, onde o grau de q1 é igual a n−1. Substituindo
x = α2 nesta igualdade, obtemos que 0 = p(α2 ) = q1 (α2 )(α2 − α1 ). Como α1 6= α2 ,
concluímos que q1 (α2 ) = 0, isto é, α2 é uma raiz de q1 . Usando agora o corolário
anterior para q1 , concluímos que q1 (x) = q2 (x)(x − α2 ), para todo x ∈ R, onde o grau
de q2 é igual a n − 2. Logo,
p(x) = q2 (x)(x − α2 )(x − α1 ),
para todo x ∈ R, onde o grau de q2 é igual a n − 2. Substituindo x = α3 nesta
igualdade, obtemos que 0 = p(α3 ) = q2 (α3 )(α3 − α2 )(α3 − α1 ). Como α1 6= α3
e α2 6= α3 , concluímos que q2 (α3 ) = 0. Prosseguindo recursivamente com este
argumento, obtemos que a função polinomial p pode ser escrita na forma (∗).
Aula 16
Pré-Cálculo
120
Teorema de D’Lambert
Corolário. Uma função polinomial de grau n não pode ter mais do que n raízes reais
distintas.
Aula 16
Pré-Cálculo
121
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
122
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
123
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
124
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
125
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
126
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
127
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
128
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
129
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
130
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
131
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
132
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
133
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
134
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
135
Exemplo
Considere a função polinomial p(x) = x 4 −3 x 3 +3 x 2 −3 x +2. Como p(1) = 0, segue-se
que α1 = 1 é raiz de p. Logo p é divisível por x − 1. Usando o dispositivo de Horner:
1
−3
3
−3
2
1
−2
1
−2
−2
1
−2
0
1
1
concluímos então que p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = q1 (x)(x − 1), onde q1 (x) =
x 3 − 2 x 2 + x − 2. Como q1 (2) = 0, segue-se que α2 = 2 é raiz de q1 . Logo q1 é divisível
por x − 2. Usando o dispositivo de Horner mais uma vez:
1
2
1
−2 1
−2
2 0
2
0 1
0
concluímos então que q1 (x) = q2 (x)(x − 2), onde q2 (x) = x 2 + 1. Portanto,
p(x) = x 4 − 3 x 3 + 3 x 2 − 3 x + 2 = (x 2 + 1)(x − 2)(x − 1).
Aula 16
Pré-Cálculo
136
O teorema fundamental da álgebra
Aula 16
Pré-Cálculo
137
O teorema fundamental da álgebra
Teorema. Toda função polinomial de grau ≥ 1 possui pelo menos uma raiz complexa.
A demonstração deste teorema requer recursos de análise.
posteriormente no curso de variáveis complexas.
Ela será feita
Definição. Dizemos que uma raiz α de uma função polinomial p tem multiplicidade m
(m ≥ 1) se p for divisível por (x − α)m e não for divisível por (x − α)m+1 . Observe que
uma raiz α tem multiplicidade m se, e só se,
p(x) = q(x)(x − α)m ,
onde q(α) 6= 0.
Corolário. Se p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 é uma função polinomial
com raízes distintas α1 , α2 , . . . , αk de multiplicidades m1 , m2 , . . . , mk , respectivamente,
então
p(x) = an (x − α1 )m1 (x − α2 )m2 · · · (x − αk )mk ,
com m1 + m2 + · · · + mk = n.
Aula 16
Pré-Cálculo
138
O teorema fundamental da álgebra
Teorema. Toda função polinomial de grau ≥ 1 possui pelo menos uma raiz complexa.
A demonstração deste teorema requer recursos de análise.
posteriormente no curso de variáveis complexas.
Ela será feita
Definição. Dizemos que uma raiz α de uma função polinomial p tem multiplicidade m
(m ≥ 1) se p for divisível por (x − α)m e não for divisível por (x − α)m+1 . Observe que
uma raiz α tem multiplicidade m se, e só se,
p(x) = q(x)(x − α)m ,
onde q(α) 6= 0.
Corolário. Se p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 é uma função polinomial
com raízes distintas α1 , α2 , . . . , αk de multiplicidades m1 , m2 , . . . , mk , respectivamente,
então
p(x) = an (x − α1 )m1 (x − α2 )m2 · · · (x − αk )mk ,
com m1 + m2 + · · · + mk = n.
Aula 16
Pré-Cálculo
139
O teorema fundamental da álgebra
Teorema. Toda função polinomial de grau ≥ 1 possui pelo menos uma raiz complexa.
A demonstração deste teorema requer recursos de análise.
posteriormente no curso de variáveis complexas.
Ela será feita
Definição. Dizemos que uma raiz α de uma função polinomial p tem multiplicidade m
(m ≥ 1) se p for divisível por (x − α)m e não for divisível por (x − α)m+1 . Observe que
uma raiz α tem multiplicidade m se, e só se,
p(x) = q(x)(x − α)m ,
onde q(α) 6= 0.
Corolário. Se p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 é uma função polinomial
com raízes distintas α1 , α2 , . . . , αk de multiplicidades m1 , m2 , . . . , mk , respectivamente,
então
p(x) = an (x − α1 )m1 (x − α2 )m2 · · · (x − αk )mk ,
com m1 + m2 + · · · + mk = n.
Aula 16
Pré-Cálculo
140
O teorema fundamental da álgebra
Teorema. Toda função polinomial de grau ≥ 1 possui pelo menos uma raiz complexa.
A demonstração deste teorema requer recursos de análise.
posteriormente no curso de variáveis complexas.
Ela será feita
Definição. Dizemos que uma raiz α de uma função polinomial p tem multiplicidade m
(m ≥ 1) se p for divisível por (x − α)m e não for divisível por (x − α)m+1 . Observe que
uma raiz α tem multiplicidade m se, e só se,
p(x) = q(x)(x − α)m ,
onde q(α) 6= 0.
Corolário. Se p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 é uma função polinomial
com raízes distintas α1 , α2 , . . . , αk de multiplicidades m1 , m2 , . . . , mk , respectivamente,
então
p(x) = an (x − α1 )m1 (x − α2 )m2 · · · (x − αk )mk ,
com m1 + m2 + · · · + mk = n.
Aula 16
Pré-Cálculo
141
O teorema fundamental da álgebra
Teorema. Toda função polinomial de grau ≥ 1 possui pelo menos uma raiz complexa.
A demonstração deste teorema requer recursos de análise.
posteriormente no curso de variáveis complexas.
Ela será feita
Definição. Dizemos que uma raiz α de uma função polinomial p tem multiplicidade m
(m ≥ 1) se p for divisível por (x − α)m e não for divisível por (x − α)m+1 . Observe que
uma raiz α tem multiplicidade m se, e só se,
p(x) = q(x)(x − α)m ,
onde q(α) 6= 0.
Corolário. Se p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 é uma função polinomial
com raízes distintas α1 , α2 , . . . , αk de multiplicidades m1 , m2 , . . . , mk , respectivamente,
então
p(x) = an (x − α1 )m1 (x − α2 )m2 · · · (x − αk )mk ,
com m1 + m2 + · · · + mk = n.
Aula 16
Pré-Cálculo
142
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
143
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
144
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
145
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
146
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
147
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
148
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
149
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
150
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
151
O teorema da decomposição em fatores irredutíveis
Lema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial cujos
coeficientes a0 , a1 , . . . , an são números reais. Se α ∈ C é uma raiz de p, então o seu
complexo conjugado α também é uma raiz de p.
Demonstração. Temos que
p(α) = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇔
p(α) = 0.
Teorema (da decomposição em fatores irredutíveis). Se p é uma função polinomial
cujos coeficientes são números reais, então p pode ser decomposta como um produto
de potências inteiras não negativas de fatores lineares (do tipo (ax + b)k , associados
às raízes reais) e/ou fatores quadráticos irredutíveis em R (do tipo (ax 2 + bx + c)k ,
associados às pares de raízes conjugadas).
Aula 16
Pré-Cálculo
152
Como calcular as raízes de uma função
polinomial?
Aula 16
Pré-Cálculo
153
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
154
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
155
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
156
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
157
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
158
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
159
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
160
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
161
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
162
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
163
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
164
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
165
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
166
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
167
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
168
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
169
Como calcular as raízes de uma função polinomial?
Se a função polinomial é de grau 1, existe uma fórmula para calcular sua
raiz.
Se a função polinomial é de grau 2, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Bhaskara”.
Se a função polinomial é de grau 3, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Tartaglia/Cardano” (ver a fórmula no
Maxima). A fórmula, contudo, não é prática.
Se a função polinomial é de grau 4, existe uma fórmula (com radicais) para
calcular sua raiz: a “fórmula de Ferrari” (ver a fórmula no Maxima).
A fórmula, contudo, não é prática.
Se a função polinomial é de grau 5, Niels Henrik Abel (1802-1829) mostrou
que não existe uma fórmula (com radicais).
Remédios: casos particulares (raízes inteiras, raízes racionais) e métodos
numéricos.
Aula 16
Pré-Cálculo
170
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
171
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
172
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
173
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
174
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
175
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
176
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
177
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
178
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
179
Pesquisa de raízes inteiras
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α ∈ Z − {0} for raiz de p, α é divisor
de a0 .
Demonstração. Se α ∈ Z − {0} é uma raiz de p, então
p(α) = 0
⇒
an αn + an−1 αn−1 + · · · + a1 α + a0 = 0
⇒
a0 = −an αn − an−1 αn−1 − · · · − a1 α
a0
= −an αn−1 − an−1 αn−2 − · · · − a1 ∈ Z.
α
⇒
Logo, se a0 /α ∈ Z, então α é um divisor de a0 .
Aula 16
Pré-Cálculo
180
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
181
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
182
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
183
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
184
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
185
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
186
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
187
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
188
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
189
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
190
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
191
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
192
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
193
Pesquisa de raízes inteiras
Exemplo. Fatore p(x) = 3x 3 −x 2 −12x +4 e resolva a inequação 3x 3 −x 2 −12x +4 ≥ 0.
Solução. Os candidatos a raiz inteira de p são os divisores inteiros de 4:
{−4, −2, −1, +1, +2, +4}
(note que 0 não é raiz de p, pois p(0) = 4 6= 0). Como
p(−4) = −156, p(−2) = 0, p(−1) = 12, p(+1) = −6, p(+2) = 0 e p(+4) = 132,
concluímos que as únicas raízes inteiras de p são −4 e +4. Logo p é divisível por
(x − 2)(x + 2) = x 2 − 4. Usando o dispositivo de Horner (ou o algoritmo da divisão de
Euclides), concluímos que
p(x) = (x − 2)(x + 2)(3 x − 1).
Para resolver a inequação p(x) = 3x 3 − x 2 − 12x + 4 ≥ 0 basta fazer o estudo de sinal
de p em sua forma fatorada: p(x) ≥ 0 ⇔ x ∈ S = [−2, 1/3] ∪ [2, +∞).
Aula 16
Pré-Cálculo
194
Pesquisa de raízes racionais
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α = m/k ∈ Q − {0} for raiz de p, com
m/k fração irredutível, então m é divisor de a0 e k é divisor de an .
Demonstração. Exercício!
Aula 16
Pré-Cálculo
195
Pesquisa de raízes racionais
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α = m/k ∈ Q − {0} for raiz de p, com
m/k fração irredutível, então m é divisor de a0 e k é divisor de an .
Demonstração. Exercício!
Aula 16
Pré-Cálculo
196
Pesquisa de raízes racionais
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α = m/k ∈ Q − {0} for raiz de p, com
m/k fração irredutível, então m é divisor de a0 e k é divisor de an .
Demonstração. Exercício!
Aula 16
Pré-Cálculo
197
Pesquisa de raízes racionais
Teorema. Seja p(x) = an x n + an−1 x n−1 + · · · + a1 x + a0 uma função polinomial com
coeficientes inteiros, isto é, a0 , a1 , . . . , an ∈ Z. Se α = m/k ∈ Q − {0} for raiz de p, com
m/k fração irredutível, então m é divisor de a0 e k é divisor de an .
Demonstração. Exercício!
Aula 16
Pré-Cálculo
198
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
1 1
3
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
199
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
1 1
3
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
200
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
1 1
3
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
201
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
1 1
3
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
202
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
1 1
3
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
203
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
1 1
3
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
204
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
205
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
206
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
207
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
208
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
209
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
210
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
211
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
212
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
213
Pesquisa de raízes racionais
Exemplo. Determine as raízes racionais de p(x) = 2x 3 − x 2 − 5x + 3.
Solução. Os divisores de a0 = 3 são {−3, −1, +1, +3} e os divisores de a3 = 2 são
{−2, −1, +1, +2}. Assim, os candidatos a raiz racional de p são
3
1 1
3
−3, − , −1, − , + , +1, + , +3
2
2 2
2
(note que 0 não é raiz de p, pois p(0) = 3 6= 0). Como
3
3
1
1
1
p (−3) = −45, p −
= , p (−1) = 5, p −
= 5, p +
= ,
2
2
2
2
2
3
p (+1) = −1, p +
= 0 e p (+3) = 33,
2
concluímos que a única raiz racional de p é +3/2. Logo p é divisível por x − 3/2.
Usando o dispositivo de Horner (ou o algoritmo da divisão de Euclides), concluímos que
p(x) = (2x 2 +2x −2)(x −3/2). Usando a “fórmula de Bhaskara” para q(x) = 2x 2 +2x −2,
obtemos que
√
√
p(x) = 2 (x + (1 − 5)/2)(x + (1 + 5)/2)(x − 3/2).
Aula 16
Pré-Cálculo
214