2012-FísicaDiscursiva_comGabarito_Pism1etapa_UFJF

UFJF – MÓDULO I DO PISM – TRIÊNIO 2012-2014 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
2
Na solução da prova, use quando necessário: g = 10 m/s .
Questão 1 – Em outubro de 2012, o austríaco
Felix Baumgartner se tornou o primeiro homem
a romper a barreira do som ao saltar de uma
cápsula, presa a um balão, a mais de 39
quilômetros acima da superfície da Terra.
Durante a queda, Baumgartner atingiu a incrível
velocidade de 1.342,8km/h. Como nessa altitude
o ar é muito rarefeito e as temperaturas são
muito baixas, ele teve que usar um traje
pressurizado.
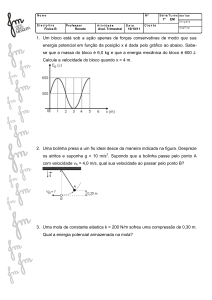
A figura ao lado resume alguns pontos
importantes desse feito. A figura não está em
escala.
Suponha que, no momento do salto, o balão
está parado em relação à superfície da Terra, e
que a velocidade inicial do paraquedista em
relação ao balão seja nula. Após atingir a
velocidade máxima em B, o paraquedista entra
numa região da atmosfera onde a resistência do
ar não pode mais ser desprezada. No trecho BC,
sua velocidade diminui devido à força de atrito com o ar. Suponha que entre os pontos B e C ele percorreu
2.558,6 metros em 15,7 segundos e a partir do ponto C entrou num regime de velocidade limite, ou seja, entre os
pontos C e D a força de atrito passou a ser igual à força da gravidade. De acordo com tais condições, calcule:
a) Quanto tempo ele levou para atingir a velocidade recorde de 1.342,8km/h. (No primeiro trecho a
resistência do ar é desprezível).
V = Vo + g .t
373
1.342,8 km / h
= 373 m / s
3,6
m
m
m
= 0, 0 + 10 2 .t
s
s
s
⇒ t = 37,3 s
b) A distância percorrida pelo paraquedista até atingir a velocidade recorde.
h = ho +
g .t 2
2
h = 0, 0m + 10
m (37, 3)2 s 2
.
s2
2
⇒
h = 6956, 45 m
c) A velocidade média do paraquedista entre os pontos C e D.
∆SCD = ∆S AD − ∆S AB − ∆S BC
∆SCD = 36575m − 6956, 45m − 2558,8m
Vm =
∆SCD = 27060, 95m ≅ 27061m
∆S
∆t
∆TCD = ∆TAD − ∆TAB − ∆TBC
∆TCD = 258s − 37,3s − 15, 7 s
∆TCD = 205s
Vm =
27061m
= 132 m/s ⇒ 475,1 km/h
205s
1
UFJF – MÓDULO I DO PISM – TRIÊNIO 2012-2014 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
Questão 2 – Newton, brincando com seu filho Einstein, constrói um pequeno canhão para lançar bolas. Para isso,
ele utiliza um tubo de plástico com 40cm de comprimento, uma mola com comprimento de 20cm e uma bola de
tênis com massa igual a 235g. A bola de tênis é colocada dentro do canhão e empurrada até que a mola se
comprima à metade do comprimento inicial, conforme figura abaixo. Considere a massa da mola desprezível.
Quando disparado na vertical, a bola atinge a altura de 90cm acima da base do canhão. Considerando que o
sistema não dissipa energia, calcule:
a) O valor da constante elástica da mola.
Considerando a origem como sendo a base, a energia total do sistema é obtida
calculando a energia no ponto mais alto a 0,9m da base:
E=
1 2
1
mv + mgh + kx 2
2
2
E = mgh
m
kg.m 2
.
0
,
9
m
=
2
,
115
s2
s2
E = 2,115 J
E = 0,235kg .10
Onde: m é a massa da bola em kg, v a velocidade no ponto mais alto em m/s, g o
2
módulo da aceleração da gravidade em m/s e h a altura em m.
Com a energia total do sistema se conserva podemos calcular a constante da mola no
ponto de maior compreensão (x = 0,1m).
1 2
1
mv + mgh + kx 2
2
2
1
E − mgh = kx 2
2
2
kg .m
m
1
2,115 2 − 0,235kg .10 2 .0,1m = k (0,1)2 m 2
s
s
2
2
kg .m
1
1,88 2 = k (0,1) 2 m 2
s
2
kg
k = 376 2 = 376 N m
s
E=
b) A velocidade com que a bola deixa o tubo em A.
No ponto A, a altura é igual a 0,4m em relação à base (origem adotada no item a). Assim,
E=
1
1
mv 2 + mgh + kx 2
2
2
1
E = mv 2 + mgh
2
kg .m 2
kg .m 2
2
=
0
,
1175
kg
.
v
+
0
,
94
s2
s2
2,115 J − 0,94 J = 0,1175kg .v 2
2,115
1,175
kg .m 2
= 0,1175kg .v 2
2
s
m2
2
v = 10 2
s
v = 10m / s
2