1 - cloudfront.net

CPV seu pé direito também na Medicina
unifesp – 17/dezembro/2010
matemática
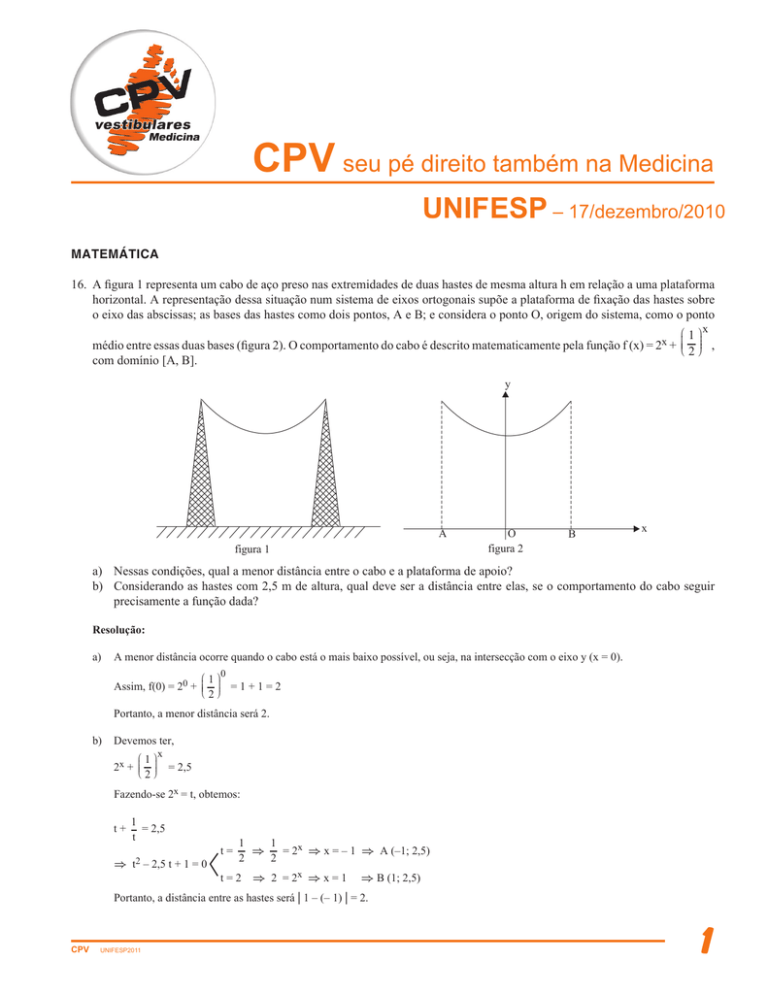
16. A figura 1 representa um cabo de aço preso nas extremidades de duas hastes de mesma altura h em relação a uma plataforma
horizontal. A representação dessa situação num sistema de eixos ortogonais supõe a plataforma de fixação das hastes sobre
o eixo das abscissas; as bases das hastes como dois pontos, A e B; e considera o ponto O, origem do sistema, como o ponto
 1 x
médio entre essas duas bases (figura 2). O comportamento do cabo é descrito matematicamente pela função f (x) = 2x +   ,
2
com domínio [A, B].
a) Nessas condições, qual a menor distância entre o cabo e a plataforma de apoio?
b) Considerando as hastes com 2,5 m de altura, qual deve ser a distância entre elas, se o comportamento do cabo seguir
precisamente a função dada?
Resolução:
a) A menor distância ocorre quando o cabo está o mais baixo possível, ou seja, na intersecção com o eixo y (x = 0).
 1 0
Assim, f(0) = 20 +   = 1 + 1 = 2
2
Portanto, a menor distância será 2.
b) Devemos ter,
 1 x
2x +   = 2,5
2
Fazendo-se 2x = t, obtemos:
1
= 2,5
t
Þ t2 – 2,5 t + 1 = 0
CPV
t+
1
1
t =Þ
= 2x Þ x = – 1 Þ A (–1; 2,5)
2
2
t = 2 Þ 2 = 2x Þ x = 1 Þ B (1; 2,5)
Portanto, a distância entre as hastes será | 1 – (– 1) | = 2. unifesp2011
1
2
unifesp – 17/12/2010
CPV seu pé direito também na Medicina
17. Progressão aritmética é uma sequência de números tal que a diferença entre cada um desses termos (a partir do segundo) e o seu
antecessor é constante. Essa diferença constante é chamada “razão da progressão aritmética” e usualmente indicada por r.
a) Considere uma PA genérica finita (a1, a2, a3, ..., an) de razão r, na qual n é par. Determine a fórmula da soma dos termos
de índice par dessa PA, em função de a1, n e r.
b) Qual a quantidade mínima de termos para que a soma dos termos da PA (–224, –220, –216, ...) seja positiva?
Resolução:
a) Pela definição dada, temos que a2 = a1 + r, a4 = a1 + 3r, a6 = a1 + 5r, ... , an = a1 + (n – 1) r
n
e assim, a sequência dos termos de índice par é uma PA de razão 2r e
termos.
2
n
( a 2 + a n ) 2 ( a1 + r + a1 + (n − 1)r ) n (2a1 + nr )n
Portanto, a soma dessa sequência será S =
=
=
4
4
2
b) Para a soma ser positiva (S > 0), temos S =
Assim,
(a1 + a n )n (−224 + (−224 + (n − 1) . 4))n
(−452 + 4n )n
=
=
2
2
2
(−452 + 4n )n
> 0 Þ n > 113. Portanto, a soma é positiva a partir de 114 termos.
2
18. Considere a1, a2, a3, b1, b2, b3 números reais estritamente positivos, tais que os pontos (a1, b1), (a2, b2) e (a3, b3) pertençam
à reta y = 2x.
a1x 2 + a 2 x + a 3
(com b1x2 + b2x + b3 ≠ 0) independe de x, pede-se determinar seu valor.
a) Sabendo-se que Q(x) =
b1x 2 + b 2 x + b3
b) Na figura, se os pontos A, B e C são vértices de um triângulo isósceles e o segmento AC é um dos diâmetros da circunferência
convenientemente centrada na origem do sistema ortogonal, pede-se determinar a medida do segmento AB em função de a1.
Resolução:
a) Como os pontos (a1, b1), (a2, b2) e (a3, b3) pertencem à reta y = 2x, temos b1 = 2a1, b2 = 2a2 e b3 = 2a3.
Assim, a1x 2 + a 2 x + a 3
a1x 2 + a 2 x + a 3
a x 2 + a 2x + a3
1
= 1
=
Þ Q (x) =
2
2
2
2
b1x + b 2 x + b3
2a1x + 2a 2 x + 2a 3
2(a1x + a 2 x + a 3 )
b) Pela figura, temos C (a1, b1) e A (–a1, –b1). Como ambos os pontos pertencem à reta y = 2x, temos que a medida do segmento AC é
AC =
Como AC é o diâmetro da circunferência, então é a hipotenusa do triângulo retângulo isóceles ABC, retângulo em B.
Assim, AB2 + BC2 = AC2 e sendo AB = BC, temos: 2AB2 = AC2 Þ 2AB2 = 20a12 Þ AB2 = 10a12 Þ AB = a1 10
CPV
unifesp2011
Q (x) =
(a1 − (−a1))2 + (b1 − (−b1))2 Þ AC
=
(2a1)2 + (2b1)2 = (2a1) 2 + (4a1) 2 = 20a12
CPV seu pé direito também na Medicina
Unifesp – 17/12/2010
3
19. No plano de Argand-Gauss (figura), o ponto A é chamado afixo do número complexo z = x + yi, cujo módulo
(indicado por | z |) é a medida do segmento OA e cujo argumento (indicado por θ) é o menor ângulo formado com OA, no
sentido anti-horário, a partir do eixo Re (z). O número complexo z = i é chamado “unidade imaginária”.
a) Determinar os números reais x tais que z = (x + 2i)4 é um número real.
b) Se uma das raízes quartas de um número complexo z é o complexo z0, cujo afixo é o ponto (0, a), a > 0, determine | z |.
Resolução:
a) z = (x + 2i)4
z = x4 + 4x3 (2i) + 6x2 (2i)2 + 4x (2i)3 + (2i)4
z = x4 + 8x3i + 24x2i2 + 32 xi3 + 16i4
z = x4 + 8x3i – 24x2 – 32 xi + 16
z = (x4 – 24x2 + 16) + (8x3 – 32x)i
Para z ser um número real, temos que 8x3 – 32x = 0 Þ 8x (x2 – 4) = 0 Þ x = 0 ou x = 2 ou x = –2
b) Como z = z04 e z0 = 0 + ai, temos:
z = (0 + ai)4 = a4i4 = a4 + 0i
Portanto, como | z | =
CPV
unifesp2011
x 2 + y 2 , temos | z | =
( a 4 ) 2 + ( 0) 2 = a 4
4
CPV seu pé direito também na Medicina
unifesp – 17/12/2010
20. Para testar a durabilidade de uma bateria elétrica foram construídos dois pequenos aparatos móveis, A e B, que desenvolvem,
respectivamente, as velocidades constantes de 30 cm/s e 20 cm/s. Cada um dos aparatos é inicialmente posicionado em uma
das duas extremidades de uma pista retilínea e horizontal de 9 m de comprimento, e correm em sentido contrário, um em
direção ao outro, cada um em sua faixa. Ao chegarem à extremidade oposta, retornam ao início, num fluxo contínuo de idas
e vindas, programado para durar 1 hora e 30 minutos. O tempo gasto pelos aparatos para virarem-se, em cada extremidade da
pista, e iniciarem o retorno rumo à extremidade oposta, é desprezível e, portanto, desconsiderado para o desenvolvimento do
experimento.
a) Depois de quantos segundos os aparatos A e B vão se encontrar, pela primeira vez, na mesma extremidade da pista?
b) Determine quantas vezes, durante toda a experiência, os aparatos A e B se cruzam.
Resolução:
a)
30 cm/s
20 cm/s
900 cm
A
B
900
900
= 30 segundos para ir de uma extremidade a outra e o aparato móvel B demora
= 45 segundos.
30
20
O aparato móvel A demora
Portanto, o primeiro encontro na mesma extremidade ocorre em, mmc (30,45) = 90 segundos.
b)
S (cm)
900
SA
SB
0
30
45
60
90
120
135
150
180
t (s)
O gráfico permite afirmar que, a cada 180s, os aparatos móveis A e B encontram-se 5 vezes e retornam ao ponto do origem.
Logo, concluímos que em 1h30 = 5400 s, os aparatos móveis encontram-se
5400 . 5
= 150 vezes.
180
Comentário da prova de matemática unifesp 2a fase 2011
A segunda fase da UNIFESP 2011 manteve o nível apresentado nos anos anteriores, com questões adequadas e conteúdos
pertinentes ao programa do Ensino Médio, tais como funções, progressões, geometria analítica, números complexos e aritmética,
que certamente contemplará os alunos bem preparados.
20% – Função Exponencial
20% – Progressão Aritmética
20% – Geometria Analítica
20% – Números Complexos
20% – Aritmética
CPV
unifesp2011