PROGRESSÃO ARITMÉTICA
CONTEÚDOS
Progressão aritmética (PA)
Razão de uma PA
Progressão aritmética crescente
Progressão aritmética decrescente
Progressão aritmética constante
Soma dos n termos de uma progressão aritmética
AMPLIANDO SEUS CONHECIMENTOS
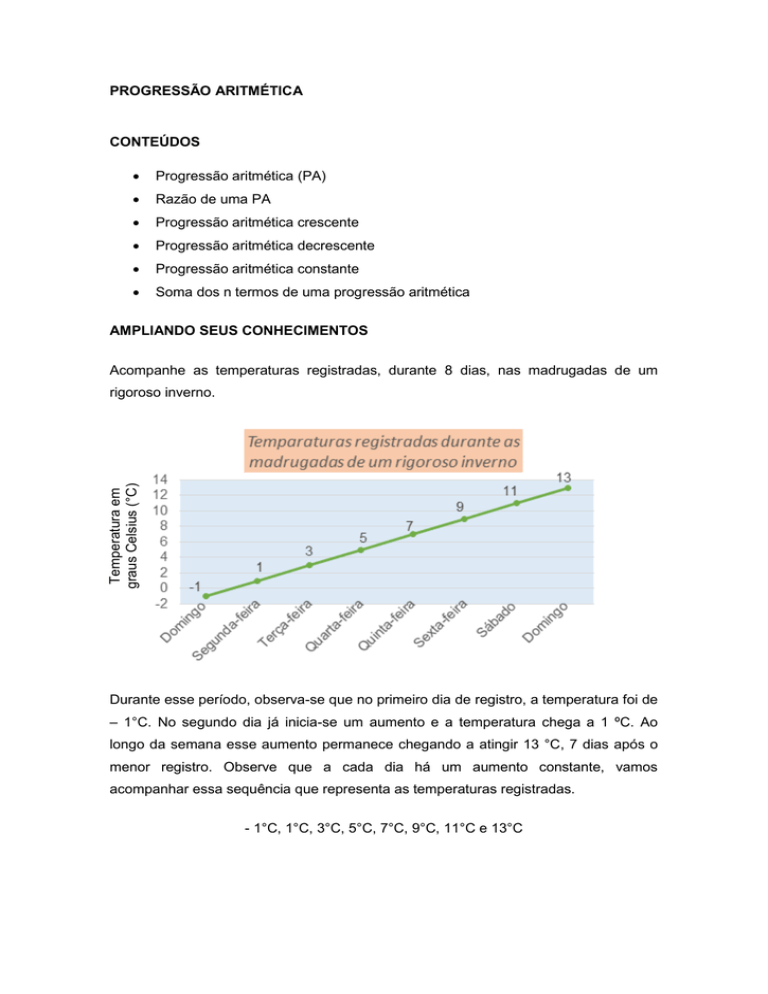
Acompanhe as temperaturas registradas, durante 8 dias, nas madrugadas de um
Temperatura em
graus Celsius (°C)
rigoroso inverno.
Durante esse período, observa-se que no primeiro dia de registro, a temperatura foi de
– 1°C. No segundo dia já inicia-se um aumento e a temperatura chega a 1 ºC. Ao
longo da semana esse aumento permanece chegando a atingir 13 °C, 7 dias após o
menor registro. Observe que a cada dia há um aumento constante, vamos
acompanhar essa sequência que representa as temperaturas registradas.
- 1°C, 1°C, 3°C, 5°C, 7°C, 9°C, 11°C e 13°C
Veja que a cada dia há um aumento de 2 °C e, se esse aumento permanecesse, na
próxima segunda-feira, a temperatura seria de 15°C. Essa sequência de registros das
temperaturas, pode receber o nome de progressão aritmética (PA).
Identifica-se uma PA quando temos uma sequência de termos em que cada termo, a
partir do segundo, é igual ao seu anterior somado uma constante.
No caso das temperaturas, temos como primeiro termo a temperatura de – 1 °C, o
segundo termo representa o primeiro registro (- 1 ºC) somado a 2 °C. E assim,
somando sempre 2 °C ao registro anterior, é dado continuidade a essa sequência de
termos.
Em uma progressão aritmética os termos podem ser identificados da seguinte
maneira:
1º termo
3º termo
5º termo
7º termo
a1 = - 1 °C
a3 = 3 °C
a5 = 7 °C
a7 = 11 °C
2º termo
4º termo
6º termo
8º termo
a2 = 1 °C
a4 = 5 °C
a6 = 9 °C
a8 = 13 °C
Cada termo ocupa uma posição, assim, sua identificação é de acordo com a posição
ocupada.
Veja que, para obter cada termo, a partir do segundo, pode-se fazer a seguinte
relação:
a2 = a1 + 2°C
a3 = a2 + 2°C
a4 = a3 + 2°C
Em uma PA, esse valor constante que é somado a cada termo, é chamado de razão.
Para conhecer a razão de uma PA basta verificar qual é a diferença entre um termo
qualquer e seu anterior. No caso discutido, observa-se:
a2 - a1
1°C - (- 1°C) = 2°C
a6 - a 5
9°C - 7°C = 2°C
a4 - a3
5°C - 3°C = 2°C
a8 - a7
13°C - 11°C = 2°C
Para obter um termo qualquer de uma progressão aritmética, utiliza-se a seguinte
expressão:
an = a1 + ( n -1) .r
Essa expressão é chamada de fórmula do termo geral de uma PA.
Vejamos um exemplo do uso da expressão an = a1 + ( n -1) .r
Vamos supor que houve o acompanhamento das temperaturas registradas na
madrugada, durante 15 dias consecutivos. No gráfico discutido no início desse
capítulo, temos o registro dos 8 primeiros dias, considerando o mesmo aumento para
os próximos dias, qual será o registro no 15º dia?
Vejamos: n = 15° dia
an = temperatura do 15° dia
r = razão, neste caso igual a 2°C.
a1 = - 1°C
a15 = - 1 °C + ( 15 - 1).2
a15 = - 1 °C + 14.2
a15 = - 1 + 28
a15 = 27
Portanto, no décimo quinto dia a temperatura registrada, durante a madrugada, seria
de 27 °C.
Essa progressão aritmética representada pelas temperaturas registradas durante a
madrugada, é identificada como uma progressão aritmética crescente. Isso porque
cada termo, é maior que seu anterior e sua razão é maior que zero.
Ao observar a relação entre os termos de uma PA, pode- se ainda fazer as seguintes
análises:
Dada uma PA de três termos representada por 3, 5, 7. Veja que se identificarmos o
segundo termo como x, temos a seguinte relação:
(x – r, x, x + r)
( 5 – 2, 5, 5 + 2)
( 3, 5, 7 )
Ou ainda, sendo o primeiro termo identificado como x, temos a seguinte relação:
(x, x + r, x + 2r)
( 3, 3 + 2, 3 + 2.2)
( 3, 5, 7)
Vejamos uma situação em que o uso dessas relações torna-se essencial.
Considere que em uma PA de três termos, a razão é um número inteiro positivo. A
soma dos termos é igual a 15 e o produto deles é igual a 80.Determine cada um dos
termos dessa PA.
Com as informações sobre a soma desses termos e o produto deles, podemos
considerar que:
( x – r) + x + ( x + r) = 15
( x – r). x. ( x + r) = 80
Se ( x – r) + x + ( x + r) = 15
temos: 3x = 15
Se ( x – r). x. ( x + r) = 80
temos: ( 5 – r). 5. ( 5 + r) = 80
5r² = 45
x=5
r² = 9 r = 3 ou r = - 3
Sendo a razão, um número inteiro positivo, devemos considerar r = 3.
Portanto, nessa PA os termos são: 2, 5, 8
Aproveitaremos essa progressão aritmética para que você observe a seguinte relação:
28
5
2
Veja que a média entre os termos extremos, resulta no termo médio, essa
situação pode ser observada para qualquer PA que tenha um número ímpar de
termos.
Veja, que essa relação pode ser observada nas seguintes progressões:
3, 10, 17,24, 31
10, 6, 2, -2, - 6
3 31
17
2
10 (6)
2
2
Progressão Aritmética decrescente.
Considere que o primeiro termo de uma PA vale 21, o segundo termo vale 18 e o
terceiro termo vale 15. Qual é a razão dessa progressão aritmética?
Observe que o segundo termo é menor que o primeiro e o terceiro, menor que o
segundo.
21, 18, 15,...
Ao realizar a subtração entre o segundo e o primeiro termo, temos:
18 – 21 = - 3
Ou seja, essa PA apresenta razão negativa.
Na situação trabalhada, temos uma PA decrescente de razão igual – 3. Observe que
cada termo, a partir do segundo, é menor que o anterior.
Em uma PA decrescente a razão será um número menor que zero.
Progressão aritmética constante
Para que seja compreendido quando uma sequência representa uma PA constante,
vamos analisar a seguinte sequência.
10, 10 ,10 ,10 ,10 ,10 ,10...
Observe que a diferença entre um termo qualquer e seu antecedente é nula. Isso
ocorre porque a razão é igual a zero.
Soma dos n termos de uma PA
Para compreender o cálculo da soma dos n termos de uma PA, vamos trabalhar com a
seguinte progressão:
1, 4, 7, 10,...
Já sabemos que essa é uma PA crescente e que sua razão é igual a 3. E, para que
seja possível determinar a soma de uma quantidade n de termos, faremos uso da
seguinte expressão:
Sn
(a 1 a n ).n
2
Suponha que deseja-se saber qual é a soma dos 4 primeiros termos dessa sequência.
Logo, temos: n = 4
a1 = 1
a4 = 10
S4
(1 10).4
2
S4
11.4
22
2
Portanto, a soma dos 4 primeiros termos dessa sequência é igual a 22.
Vamos aplicar a soma dos n termos de uma PA em uma situação relacionada ao
cotidiano de um atleta.
Imagine que uma atleta deseja aumentar diariamente seu desempenho. Em
determinado dia esse atleta correu 30 km, e decidiu que a partir de então, por um
período de 30 dias, em cada dia, ele iria correr 1 km a mais que o dia anterior. Após o
30° dia, somando todos os quilômetros corridos diariamente, quantos quilômetros o
atleta correu?
Para encontrar a resposta para a situação colocada, é preciso lembrar que essa é uma
PA de 31 termos, isso porque o primeiro termo é representado pelos 30 km. Além
disso, é preciso lembrar que não temos o valor do 31° termo, logo, antes de calcular a
soma de todos os termos, é preciso calcular o a31:
an = a1 + ( n -1) .r
a31 = 30 + ( 31 – 1) . 1
a31 = ?
a31 = 30 + 30.1
a1 = 30
a31 = 30 + 30
a31 = 60
n = 31
r=1
Conhecido o valor do último termo, é possível calcular a soma de todos os termos da
PA.
Sn
(a 1 a n ).n
2
S31= ?
a1 = 30
S31 =
(30 60).31
2
S31 =
90.31
2
S31 =
2.790
2
a31 = 60
n = 31
S31= 1.395
Após os 30 dias o atleta terá corrido 1.395 km.
ATIVIDADES
1. Observe a sequência, verifique se ela é uma PA, e caso positivo, identifique sua
razão.
3, 7, 11,15, 19, 23,...
2. Numa PA de razão 2, o 1º termo é 8. Que posição ocupa o termo cujo valor é 56?
3.(ENEM – 2012)Jogar baralho é uma atividade que estimula o raciocínio. Um jogo
tradicional é a Paciência, que utiliza 52 cartas. Inicialmente são formadas sete colunas
com as cartas. A primeira coluna tem uma carta, a segunda tem duas cartas, a terceira
tem três cartas, a quarta tem quatro cartas, e assim sucessivamente até a sétima
coluna, a qual tem sete cartas, e o que sobra forma o monte, que são as cartas não
utilizadas nas colunas.
A quantidade de cartas que forma o monte é
a) 21.
b) 24.
c) 26.
d) 28.
e) 31
4. ( Saresp – 2007) Considere o evento: "Um atleta corre sempre 200 metros a mais
do que no dia anterior". É verdade que, o número de metros percorridos a cada dia,
constituem os termos de uma progressão
a) geométrica de razão 2.
b) aritmética de razão 2.
c) geométrica de razão 200.
d) aritmética de razão 200.
5. O valor da soma de todos os múltiplos positivos de 10, formados por dois
algarismos, está indicado na alternativa
a) S = 150
b) S = 250
c) S = 350
d) S = 450
e) S = 850
6. (ENEM – 2013) O ciclo de atividade magnética do Sol tem um período de 11 anos.
O início do primeiro ciclo registrado se deu no começo de 1755 e se estendeu até o
final de 1765. Desde então, todos os ciclos de atividade magnética do Sol têm sido
registrados.
Disponível em: http://g1.globo.com. Acesso em: 27 fev. 2013.
No ano de 2101, o Sol estará no ciclo de atividade magnética de número
a) 32.
b) 34.
c) 33.
d) 35.
e) 31.
LEITURA COMPLEMENTAR
Gauss, O Príncipe da Matemática
Um professor, para manter seus alunos ocupados,
mandou que somassem todos os números de um a
cem. Esperava que eles passassem bastante tempo
executando a tarefa. Para sua surpresa, em poucos
instantes um aluno de sete ou oito anos chamado
Gauss deu a resposta correta: 5.050. Como ele fez a
conta tão rápido? Gauss observou que se somasse o
primeiro número com o último, 1 + 100, obtinha 101.
Se somasse o segundo com o penúltimo, 2 +
99, também obtinha 101.
Figura 1 - Carl Friedrich Gauss
Fonte: Wikimedia Commons
Somando o terceiro número com o antepenúltimo, 3 + 98, o resultado também era
101. Percebeu então que, na verdade, somar todos os números de 1 a 100
correspondia a somar 50 vezes o número 101, o que resulta em 5.050. E assim, ainda
criança Gauss inventou a fórmula da soma de progressões aritméticas. (...)
Gauss percebeu rapidamente que a soma de todos os números de 1 a 100 resulta em
5.050. Para isso, vamos somar os termos de dois em dois, de uma forma bem
especial. Veja:
1
+ 100 = 101,
2
+ 99 = 101,
3
+ 98 = 101,
4
+ 97 = 101,
.
.
.
47 + 54 = 101,
48 + 53 = 101,
49 + 52 = 101,
50 + 51 = 101.
Nas somas acima, ocupando o lugar da primeira parcela temos todos os números de 1
a 50. No lugar da segunda parcela, temos todos os números de 51 a 100. São 50
somas e cada uma delas resulta sempre no mesmo número: 101. Portanto, para
somar todos os números de 1 a 100 basta somar 50 vezes 101, isto é, calcular 50 x
101 = 5050.
(...) Gauss viveu entre 1777 e 1855 e foi sem dúvida um dos maiores matemáticos que
já existiram. É por muitos considerado o maior gênio matemático de todos os tempos,
razão pela qual também é conhecido como o Príncipe da Matemática.
Disponível em:<http://www.uff.br/sintoniamatematica/curiosidadesmatematicas/curiosidadesmatematicashtml/audio-gauss-br.html>. Acesso em: 28 mar. 2016. 12h.
INDICAÇÕES
Para estudar um pouco mais as progressões aritméticas, consulte os links indicados
a seguir.
Podcast – Progressões aritméticas
Disponível
em:
http://www.eja.educacao.org.br/bibliotecadigital/matematica/podcasts/Lists/Podcast/Dis
pForm.aspx?ID=19&Source=http%3A%2F%2Fwww%2Eeja%2Eeducacao%2Eorg%2E
br%2Fbibliotecadigital%2Fmatematica%2Fpodcasts%2FPaginas%2FPodcastEM%2Ea
spx
Atividade podcast: Progressões aritméticas
Disponível em:
http://www.eja.educacao.org.br/bibliotecadigital/matematica/podcasts/Lists/Podcast/Dis
pForm.aspx?ID=19&Source=http%3A%2F%2Fwww%2Eeja%2Eeducacao%2Eorg%2E
br%2Fbibliotecadigital%2Fmatematica%2Fpodcasts%2FPaginas%2FPodcastEM%2Ea
spx
Progressão aritmética – Para correr a São Silvestre
Disponível em: http://m3.ime.unicamp.br/recursos/1150.
REFERÊNCIAS
BARRETO FILHO, Benigno. BARRETO, Cláudio Xavier. Matemática aula por aula.
São Paulo: FTD, 2000.
CECIERJ, Fundação. Matemática e suas Tecnologias – Módulo III/ Matemática. Rio
de Janeiro, 2013. Disponível em: <http://projetoseeduc.cecierj.edu.br/eja/materialaluno/modulo-03/Miolo_Matematica_Nova_Eja_Aluno_Mod03.pdf>. Acesso em: 29
mar. 2016. 10h.
ENEM 2012 – Exame Nacional do Ensino Médio. INEP – Instituto Nacional de
Estudos e Pesquisas Educacionais Anísio Teixeira. Ministério da Educação. Disponível
em:<http://download.inep.gov.br/educacao_basica/enem/provas/2012/caderno_enem2
012_dom_amarelo.pdf>.Acesso em: 29 mar. 2016. 9h
ENEM 2013 – Exame Nacional do Ensino Médio. INEP – Instituto Nacional de
Estudos e Pesquisas Educacionais Anísio Teixeira. Ministério da Educação. Disponível
em:<http://download.inep.gov.br/educacao_basica/enem/provas/2013/caderno_enem2
013_dom_amarelo.pdf>.Acesso em: 29 mar. 2016. 15h
SARESP 2007 – Sistema de Avaliação do Rendimento Escolar do estado de São
Paulo. SEE/SP. Disponível
em:<http://saresp.fde.sp.gov.br/2007/Arquivos/Provas%202007/Matem%C3%A1tica/E
M%203%C2%AA%20s%C3%A9rie/1_Manh%C3%A3/Prova-MAT-3EMManha.pdf>Acesso em: 28 mar. 2016. 12h.
SMOLE, Kátia Stocco; DINIZ, Maria Ignez. Matemática Ensino Médio, v 2: livro do
professor. 6ª ed. São Paulo: Saraiva, 2010. p. 222 - 260.
UNIVERSIDADE FEDERAL FLUMINENSE. Gauss, O Príncipe da Matemática.
Disponível
em:<http://www.uff.br/sintoniamatematica/curiosidadesmatematicas/curiosidadesmate
maticas-html/audio-gauss-br.html>. Acesso em: 29 mar. 2016. 13h.
WIKIMEDIA COMMONS. Carl Friedrich Gauss. Disponível em:
<https://commons.wikimedia.org/wiki/Johann_Carl_Friedrich_Gau%C3%9F#/media/Fil
e:Carl_Friedrich_Gauss.jpg>. Acesso em: 30 mar. 2016. 9h15.
GABARITO
1. Uma PA é uma sequência de termos em que cada termo, a partir do segundo é a
soma do termo anterior com uma constante. Na sequência apresentada, observa-se
que a partir do primeiro, para obter cada termo, é somado o valor 4. Portanto, essa é
uma PA de razão 4.
2. Neste caso, deseja-se descobrir a posição de um determinado termo, conhecendo o
valor dele, a razão e o primeiro termo da PA, tem-se:
an = a1 + ( n -1) .r
an = 56
a1 = 8
n=?
r=2
56 = 8 + ( n -1) .2
50 = 2n
56 = 8 + 2n – 2
n
50
2
56 = 2n + 6
56 - 6 = 2n
n = 25
Portanto, a posição ocupada pelo termo de valor igual a 56 é a 25°.
3. Alternativa correta é a letra B.
Para saber qual é a quantidade de cartas que tem no monte, pode-se utilizar a soma
dos n termos de uma PA. Neste caso, vamos calcular apenas qual é a soma das
cartas que estão nas 7 colunas.
Sn
(a 1 a n ).n
2
S7
(1 7).7
2
S7
8.7
= 28
2
Nas 7 colunas há um total de 28 cartas. Se o jogo tem 52 cartas, há no monte um
total de 24 cartas.
52 – 28 = 24
4. Alternativa correta é a letra D.
Se a cada dia o atleta corre 200 metros a mais que o dia anterior, o número de metros
percorridos representa uma progressão aritmética de razão 200.
5. A alternativa correta é a D
O menor múltiplo de 10 que tem 2 algarismos é o próprio 10. O maior múltiplo de 10
que tem 2 algarismos é o número 90. Considerando os números de 2 algarismos, são
múltiplos de 10 os números que apresentam o algarismo zero na unidade. Assim, temse:
10, 20, 30, 40, 50, 60 ,70 ,80 e 90. Para calcular a soma desses números
podemos utilizar a soma dos termos de uma PA.
Sn
(a 1 a n ).n
2
S9
(10 90).9
2
S9
100.9
450
2
6. Se o ciclo tem um período de 11 anos, esse valor representa a razão dessa PA.
Considerando que o primeiro termo dessa PA é 1755, e deseja-se saber a posição do
termo de valor igual a 2101, temos:
2101 – 1755 = 346
346
= 31, 45 (aproximadamente)
11
Portanto, em 2101 o Sol estará no 32° ciclo de atividade magnética, pois de acordo
com os cálculos já terá passado o 31º ciclo.










