“Educa teu filho no caminho que deve andar, e quando grande não

“Educa teu filho no caminho que deve andar, e quando grande não se desviará dele” Prov.22.6
Bateria de Exercícios
Data: 22/5/15
Turma: Básico
Área II
Matemática – Básico A
1) Uma fábrica tem a capacidade máxima de produzir por mês 400 unidades de um determinado
produto. O custo desta fábrica é composto por um valor fixo de R$ 600,00 mais um valor variável,
por unidade, de R$ 4,50. ( y = 600 + 4,5x ) Quando a produção supera 200 unidades, o valor fixo
não muda, mas o valor variável por unidade cai para R$ 3,00 ( y = 600 + 3x). Sendo assim,
determine a relação entre o custo mensal C da fábrica e o número x de unidades produzidas no
mês.
2) Considere a função real definida por:
3) Determine a paridade das seguintes funções:
a) f(x) = x² + 4
b) f(x) = x² + 4x
c) f(x) = x³ - 1
4) Se f(x) = 3x – 4 e f(g(x)) = 6x²+ 3x – 1, determine g(x):
5) Se f(x) = 3x² + x – 5, calcule o valor de fof ( 1):
Matemática – Básico B
Para resolver as questões 1 e 2, consulte as páginas 106 e 107 do livro texto.
1) .
Dadas as funções
e
, calcule:
a)
b)
c)
d) Podemos dizer que a função
é uma função par? Justifique.
2)
Dada a função
, calcule:
a)
b)
c)
d) Podemos dizer que
3) Dada a função
é uma função ímpar? Justifique.
, a expressão da função inversa
é:
a)
b)
c)
d)
4) Determine o conjunto imagem da inversa da função bijetora
.
5) Dada as funções
e
, calcule
.
Geometria
1. Sabendo que o triângulo abaixo é isósceles de base AC determine o valor de “x”.
a) 75º
b) 30º
c) 120º
d) 95º
2.
Dado um triângulo equilátero com perímetro igual a 111cm. Qual é o lado deste triângulo?
a) 333cm
b) 36cm
c) 37cm
d) 46cm
3. Na figura abaixo, AD é bissetriz. Calcule a e b:
A
a
50º
30º
B
b
D
C
4. Classifique os triângulos abaixo:
QUANTO AOS LADOS
QUANTO AOS ÂNGULOS
(
) Equilátero
(
) Isósceles
( ) Obtusângulo
(
) Escaleno
(
QUANTO AOS LADOS
( ) Acutângulo
) Retângulo
QUANTO AOS ÂNGULOS
(
) Equilátero
( ) Acutângulo
(
) Isósceles
( ) Obtusângulo
(
) Escaleno
( ) Retângulo
5. Determine o valor de “x”, lembrando que segmentos com “marcas iguais” são congruentes .
sabendo que MN = NO
Biologia
1- gráfico representa a atividade enzimática de uma determinada reação em função da temperatura:
A seta indica o ponto:
a) ótimo de temperatura para a atividade enzimática.
b) de desnaturação da enzima.
c) de desnaturação do produto.
d) mínimo da temperatura para a reação enzimática.
2- Um estudante recebeu um quebra-cabeça que contém peças numeradas de 1 a 6 representando partes de
moléculas.
Para montar a estrutura de uma unidade
fundamental de uma proteína, ele deverá juntar três
peças do jogo na seguinte sequência:
a) 1, 5 e 3
b) 1, 5, e 6
c) 4, 2 e 3
d) 4,2 e 6
3- Um aluno após ter estudado a organização celular de um procarionte e a de um eucarionte, construiu outra
tabela, usando os seguintes sinais: (+) significa presença e (-) ausência da estrutura.
Célula
Estrutura
De procarionte
De eucarionte
Núcleo
(-)
(+)
Ribossomo
(+)
(+)
Membrana celular
(+)
(+)
Cromossomos
(-)
(+)
Mitocôndria
(+)
(+)
Complexo glogiense
(-)
(+)
Indique os erros cometidos por este aluno.
_______________________________________________________________________________________
_______________________________________________________________________________________
4- Considere as características das células A, B e C indicadas na tabela abaixo, relacionadas à presença (+) ou
ausência (-) de alguns componentes, e responda:
COMPONENTES CELULARES
Células
Parede
celular
Envoltório Nucléolo
nuclear
Ribossomos Complexo
golgiense
Mitocôndrias Cloroplastos
A
-
+
+
+
+
+
-
B
+
+
+
+
+
+
+
C
+
-
-
+
-
-
-
Quais das células A, B e C são eucarióticas e quais são procarióticas? Justifique a sua resposta.
_______________________________________________________________________________________
_______________________________________________________________________________________
5- Por que as enzimas são importantes para o nosso organismo?
_______________________________________________________________________________________
_______________________________________________________________________________________
Física
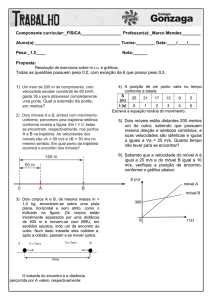
1- Um móvel se desloca, em movimento uniforme, sobre o eixo x durante o intervalo de tempo de t0 = 0
a t = 30 s. O gráfico representa a posição x, em função do tempo t, para o intervalo de t = 0 a t = 5,0 s.
O instante em que a posição do móvel é = 30 m, em segundos, é
a) 10
d) 25
b) 15
e) 30
c) 20
2-Um móvel se desloca em MRU, cujo gráfico v = t está representado no gráfico. Determine o valor do
deslocamento do móvel entre os instantes t = 2,0 s e t = 3,0 s.
a) 0
b) 10 m
c) 20 m
d) 30 m
e) 40 m
3- Os gráficos referem-se a movimentos unidimensionais de um corpo em três situações diversas,
representando a posição como função do tempo. Nas três situações, são iguais
a) as velocidades médias.
b) as velocidades máximas.
c) as velocidades iniciais.
d) as velocidades finais.
e) os valores absolutos das velocidades máximas.
4- O gráfico representa a velocidade escalar de um corpo, em função do tempo
De acordo com o gráfico, o módulo da aceleração desse corpo, em metros por segundo ao quadrado, é
igual a
a) 0,50
b) 4,0
c) 8,0
d) 12,0
e) 16,0
5- As velocidades de crescimento vertical de duas plantas, A e B, de espécies diferentes, variaram, em
função do tempo decorrido após o plantio de suas sementes, como mostra o gráfico.
É possível afirmar que:
a) A atinge uma altura final maior do que B
b) B atinge uma altura final maior do que A
c) A e B atingem a mesma altura final
d) A e B atingem a mesma altura no instante t0
e) A e B mantêm altura constante entre os instantes t1 e t2