Lista1: Cinemática Unidimensional

Problemas propostos
Questões em Aula
Questões Conceituais
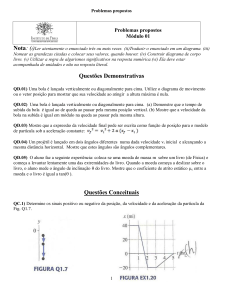
QC.1) Determine os sinais positivo ou negativo da posição, da velocidade e da aceleração da partícula da
Fig. Q1.7.
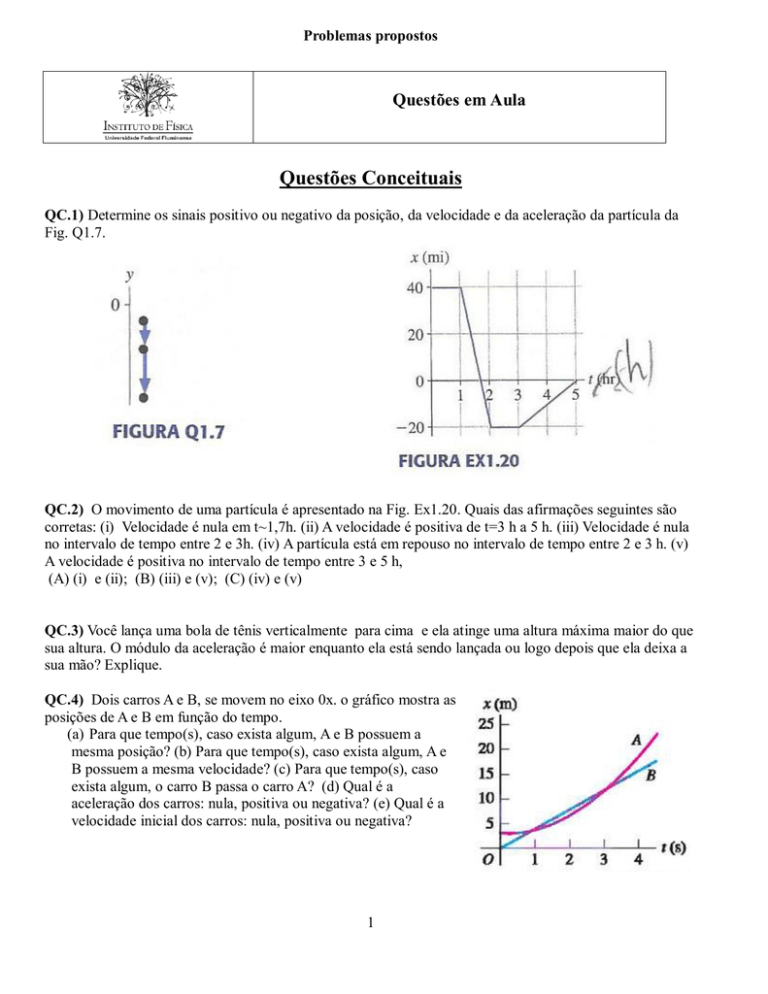
QC.2) O movimento de uma partícula é apresentado na Fig. Ex1.20. Quais das afirmações seguintes são
corretas: (i) Velocidade é nula em t~1,7h. (ii) A velocidade é positiva de t=3 h a 5 h. (iii) Velocidade é nula
no intervalo de tempo entre 2 e 3h. (iv) A partícula está em repouso no intervalo de tempo entre 2 e 3 h. (v)
A velocidade é positiva no intervalo de tempo entre 3 e 5 h,
(A) (i) e (ii); (B) (iii) e (v); (C) (iv) e (v)
QC.3) Você lança uma bola de tênis verticalmente para cima e ela atinge uma altura máxima maior do que
sua altura. O módulo da aceleração é maior enquanto ela está sendo lançada ou logo depois que ela deixa a
sua mão? Explique.
QC.4) Dois carros A e B, se movem no eixo 0x. o gráfico mostra as
posições de A e B em função do tempo.
(a) Para que tempo(s), caso exista algum, A e B possuem a
mesma posição? (b) Para que tempo(s), caso exista algum, A e
B possuem a mesma velocidade? (c) Para que tempo(s), caso
exista algum, o carro B passa o carro A? (d) Qual é a
aceleração dos carros: nula, positiva ou negativa? (e) Qual é a
velocidade inicial dos carros: nula, positiva ou negativa?
1
Problemas propostos
QC. 5) Um pêndulo simples ( um corpo oscilando na extremidade de um fio) descreve um arco do círculo
em cada oscilação. Qual é a direção e o sentido da aceleração nas extremidades da oscilação? E no ponto
médio?
QC.6) Em um movimento circular uniforme, como varia a aceleração quando a velocidade cresce de um
fator igual a 3? Quando o raio decresce de um fator igual a 2?
QC.7) Quando as duas extremidades de uma corda são puxadas com forças de mesmo módulo mas de
sentidos contrários, por que a tensão na corda não é igual a zero?
QC.8) Você amarra um tijolo na extremidade de uma corda e o faz girar em torno de você em um círculo
horizontal. Descreva a trajetória quando você larga repentinamente a corda.
QC.9) Quando um peso grande é suspenso por um fio no limite de sua elasticidade, puxando-se o fio
suavemente o peso pode ser levantado ; porém, se você puxar bruscamente , o fio se rompe. Explique isso
usando as leis de Newton do movimento.
QC.10) Para fazer um carro parar em uma estrada com gelo é melhor pisar forte no pedal do freio para
travar as rodas e fazê-las deslizar ou pisar lentamente no pedal de modo que as rodas continuem a rolar?
Por quê ?
QC.11) Um bloco de massa m é mantido estacionário sobre uma rampa pela força de atrito que a rampa
exerce sobre ele. Uma força F, dirigida para cima ao longo da rampa, é então aplicada ao bloco e sua
intensidade gradualmente aumentada a partir do zero. Durante esse aumento o que acontece com a direção,
o sentido e a intensidade da força de atrito que age sobre o bloco?
Questões Objetivas
QO.1) Um ovo é atirado verticalmente para cima de um ponto próximo da cornija na extremidade superior
de um edifício alto. Ele passa rente da cornija em seu movimento descendente, atingindo um ponto a 50,0 m
abaixo da cornija 5,0 s após ele abandonar a mão do lançador. Despreze a resistência do ar. (a) Calcular a
velocidade inicial do ovo. (b) Qual a altura máxima atingida acima do ponto inicial do lançamento? (c)
Qual o módulo da velocidade nessa altura máxima? (d) Qual o módulo e o sentido da aceleração nessa
altura máxima? (e) Faça gráficos de a versus t, v versus t e y versus t para o movimento do ovo.
Resp. (a) 14,5 m/s; (b) 10,7m; (c) vy=0; (d) 9,80 m/s2; para baixo e em todo o movimento.
2
Problemas propostos
QO.2) Uma pessoa deixa cair uma melancia do alto do telhado de um edifício. Ele escuta o barulho da
melancia ao se espatifar 2,20 s depois do lançamento. Qual a altura do edifício? A velocidade do som no ar
é igual a 340 m/s. Despreze a resistência do ar. (Resp. 28,6 m. )
QO.3) Um rapaz lança um fósforo aceso no topo de uma lixeira cilíndrica (diâmetro D e altura 2D) vazia.
Para tornar esse evento mais esportivo, a aparte inferior da lixeira está no mesmo nível do ponto em que o
fósforo deixa a mão, e a lixeira está uma distância horizontal de 6D do ponto em que o fósforo deixa a mão
do rapaz. Ele lança o fósforo com ângulo de 45,0o acima da horizontal. Ache o valor máximo e o valor
mínimo da velocidade inicial do lançamento para o fósforo entre pela parte superior da lixeira. Despreze a
resistência do ar e dê sua resposta em termos de g e de D.
QO.4) Um projétil é lançado com velocidade vo formando um ângulo o com a horizontal. O ponto de
lançamento está situado a uma altura h acima do solo. Desprezando a resistência do ar, mostre que a
distância horizontal percorrida pelo projétil antes de ele atingir o solo é dada por
x


vo cos  o
vo sen o  vo 2 sen 2 o  2 gh .
g
QO.5) Um motoqueiro salta sobre um rio com sua motocicleta. A rampa de decolagem é inclinada de
53,0o, largura do rio é de 40,0m, e a outra margem está a 15,0m abaixo do nível da rampa. O rio está a
100m abaixo do nível da rampa. Despreze a resistência do ar. .
(a) Qual deve ser sua velocidade para que ele possa alcançar a
outra margem sem cair no rio? (b) Caso sua velocidade for
igual à metade do valor encontrado em (a), onde ele cairá?
Resp (a) 17,8 m/s; (b) cairá no rio, a uma distância 28,4 m da
margem próxima da rampa.
QO.6) Em um filme de aventura, o herói joga uma granada de se carro, que se desloca a 90,0km/h,
atingindo o carro do inimigo, que se desloca a 110,0km/h. O carro do inimigo está a 15,8 m à frente do
carro do herói quando ele joga uma granada. Se o lançamento é tal que sua velocidade inicial em relação a
ele forma um ângulo de 450 acima da horizontal, qual deve ser o módulo da velocidade inicial? Os dois
carros se deslocam no mesmo sentido numa estrada retilínea e plana. Despreze a resistência do ar. Ache o
módulo da velocidade inicial em relação ao herói e em relação à Terra.
Resp: 61,2 km/h em relação ao herói; 140km/h em relação à Terra.
3
Problemas propostos
QO.7) Duas caixas, uma de massa de 4,00 kg e outra de 6,00 kg, estão em repouso sobre uma superfície
áspera, ligadas por uma corda leve. O coeficiente de atrito cinético é de 0,25. Uma mulher usando um tênis
áspero (de modo que ela possa exercer tração sobre o solo) puxa horizontalmente a caixa de 6,00 kg com
uma força que produz uma aceleração de 2,50 m/s2. (a) Qual é o módulo da força F? (b) Qual é a tensão T
que conecta as duas caixa?
QC.8) Um objeto com massa m se move ao longo do eixo Ox. Sua posição em função do tempo é dada por
x(t) = A t – B t3, onde A e B são constantes. Calcule a força sobre o objeto em função do tempo.
QC.9) (Lista 4) Um bloco A, com peso 3P, desliza sobre um plano inclinado S com inclinação de 36,9 0 a
uma velocidade constante, enquanto a prancha B, com peso P, está em
repouso sobre A. A prancha está ligada por uma corda no topo do plano.
Ver a figura. (a) Faça um diagrama de todas as forças que atuam sobre A.
(b) Se o coeficiente de atrito cinético entre A e B for igual ao coeficiente de
atrito cinético entre S e A, calcule o seu valor.
Resp. (b) 0,75
QC.10) Um bloco de massa m1 está sobre um plano inclinado com um ângulo de inclinação  e está ligado
por uma corda que passa sobre uma polia pequena a um segundo bloco suspenso de massa m2. O
coeficiente de atrito cinético é c e o coeficiente de atrito estático é e. (a) Ache a massa m2 para a qual o
bloco de massa m1 sobe o plano com velocidade constante de
pois que ele entra em movimento. (b) Ache a massa m2 para a
qual o bloco de massa m1 desce o plano com velocidade
constante de pois que ele entra em movimento. (c) Para que
valores de m2 os blocos permanecem em repouso depois de
eles serem libertados a partir do repouso?
Resp.(a) m2  m1 (sen  c cos  ) ;
(b) m2  m1 (sen  c cos  ) ;
(c) m2  m1 (sen  e cos  ) , maior;
m2  m1 (sen  e cos  ) , menor.
4
Problemas propostos
QC.11) Um bloco de massa M é amarrado na extremidade inferior de uma corda de massa m e
comprimento L. Uma força F constante é aplicada de baixo para cima na extremidade superior da corda,
fazendo com que o bloco e a corda sejam acelerados para cima. Encontre a tensão na corda a uma distância
x da sua extremidade superior, onde x pode ter qualquer valor entre 0 e L.


mx
Resp. T ( x)  F 1 

 L( m  M ) 
QC.12) Determine a aceleração de cada bloco da figura em função de m1,
de m2 e de g. Não existe nenhum atrito em nenhuma parte do sistema.
Resp.: a1 = 2 a2; a2 = m2g /(4 m1 + m2)
QC.13) Um bloco de massa m1 colocado sobre uma superfície horizontal e áspera está conectado a uma
bola de massa m2 através de uma corda leve que passa pela polia sem
atrito. Uma força de magnitude F inclinada de um ângulo  com a
horizontal é aplicada sobre o bloco de m1. O coeficiente de atrito cinético
é c. Determine o módulo da aceleração dos blocos.
F (cos   c sen )  g (m2  c m1 )
Resp: a 
m1  m2
QC.14) Na figura uma prancha de massa m1=40 kg repousa sobre um piso sem atrito, o bloco de massa
m2=10 kg repousa sobre o topo da prancha. O coeficiente de atrito estático entre o bloco e a prancha é de
0,60, e o coeficiente de atrito cinético é de 0,40. O bloco é puxado por uma força horizontal F de
intensidade 100N. (a) Mostre que o bloco deslizará sobre a prancha. Na notação de vetor unitário, quais são
as acelerações resultantes (b) do bloco e (c) da prancha?
Resp.: (b) a = - 6,1 i m/s2 ,(c) a = - 0,98 i m/s2
QO.15) Um brinquedo de parque de diversão consiste em um carro se movendo em uma circunferência
vertical na extremidade de uma haste rígida de massa desprezível. O peso conjunto do carro com os
passageiros é de 5,0 kN e o raio da circunferência é de 10 m. No topo da circunferência, quais são (a) o
módulo FH e (b) o sentido (para cima ou para baixo) da força exercida pela haste sobre o carro se a
velocidade do carro é v=5,0 m/s. (c) Repetir os itens (a) e (b) se v = 12 m/s.
Resp. (a) e (b): 3,7 kN, para cima; (c) 2,3kN, para baixo.
5