O-Ângulo-e-o-Tempo

1
Matemática Geometria Euclidiana
O Ângulo e o Tempo
Autor: Professor Maurício Ary Jalom
Bacharel e Licenciado em Matemática, Física e Desenho, pela
Faculdade de Filosofia, Ciências e Letras da
Universidade do Estado do Rio de Janeiro.
Ex-Professor da CEFET-RJ
Ex-Professor da Escola Técnica Estadual “Visconde de Mauá”
Ex-Professor do Curso Preparatório Unipré
Ex-Professor do PEJA-2 (CIEP “Samuel Wainer”)
Ex-Professor do Colégio Estadual “F.A. Raja Gabaglia”
Ex-Professor da E.M. “Charles Dickens”
Ex-Professor da E.M. “Carneiro Felipe”
E-Mail: [email protected]
Conteúdo: Ângulos e Tempo – Definições - Formula original
Público-Alvo: Professores de Matemática, estudantes do Ensino
Fundamental, e interessados em geral.
Data: 09/02/2008
O Ângulo e o Tempo
Lecionei muitos anos no Curso Unipré (Preparatório para Concursos para as Fõrças
Armadas) e numa das aulas de Geometria Euclidiana estávamos focalizando exercícios
para obtenção de ângulos formados pelos ponteiros de relógios.
Eu ia resolvendo e explicando pelos procedimentos costumeiros, quando um aluno me
mostrou uma fórmula que "matava"qualquer exercicio deste assunto.
A fórmula era â=30°.H - 5,5.M Sendo H (horas) e M (MINUTOS)
Comecei a aplicar a fórmula oferecida pelo aluno e ví que realmente era infalível, e
tornava rápida a solução.
Fíz ao aluno 2 perguntas:
1) Quem te mostrou esta fórmula?
2) Voce sabe como foi idealizada a fórmula?
A resposta à 1ª pergunta foi a de que aprendera num curso que tinha feito anteriormente.
 2ª resposta foi simplesmente: sei aplicar, mas não sei justificar.
Sinceramente maravilhado pela eficiência da fórmula, decidí decifrá-la, e no dia seguinte
mostrei à turma a justificação da mesma.
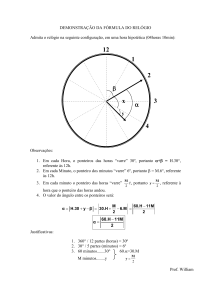
1º) O ângulo formado pelos 2 ponteiros do relógio, é simplesmente a diferença entre os
trajetos (arcos) descritos pelos 2 ponteiros desde o ½ dia (quando os ponteiros estavam
coincidentes), isto é formando um ângulo de 0°, até a hora estabelecida para determinar
o ângulo por eles formado.
2
2º) É preciso saber que a medida do arco percorrido pelo ponteiro maior vale 12 vezes a
medida do arco percorrido pelo menor ponteiro, numa mesma medida do tempo, pois
assim funciona e foi feito o mecanismo do relógio.
3º) O mostrador de um relógio é uma circunferência, na qual uma volta completa feita
por qualquer móvel é de 360°,
Os nºs do mostrador 1,2,3,4, etc. distam de 1/12 desta medida, isto é 30°.
4º) Pelo que foi exposto, em um minuto de tempo, o ponteiro maior percorre um arco
de (30/5)° = 6 °
Neste mesmo intervalo de tempo o menor ponteiro percorrerá (6/12)° = (1/2)°
Percebe-se então que em um minuto de tempo, o maior ponteiro se avantaja em relação
ao menor ponteiro de 5,5°.
Surgimento da Fórmula
É uma corrida pelo tempo e para rápida compreensão, vamos estabelecer que queremos
saber o ângulo formado pelos ponteiros do relógio, quando ele marca 2h15m.
Começa o movimento dos ponteiros partindo de ½ dia.
Imaginemos exatamente o relógio marcando 2h00m,
O que aconteceu?
O ponteiro menor percorreu 60° e o ponteiro maior deu 2 voltas completas e retornou
ao nº 12 ou 0°.
Agora finalmente às 2h15m, o ponteiro maior percorreu 90° e o ponteiro menor
percorreu (90/12)° = 7,5° = 7°30’ (medida de arco ou ângulo) pois o ângulo é central.
O problema já fica práticamente resolvido, mas o que nos interessa é mostrar o papel
que a fórmula faz.
Travemos neste instante o relógio, e vamos recuar os 2 ponteiros de uma mesma
medida que será o arco 7°30’, ora isto só é possível fazer com o relógio paralisado,
senão não poderíamos efetuar este igual recuo entre os ponteiros, pois a marcha dos
dois nunca é a mesma.
Aí o leitor perguntará, e daí?
Daí é que o ponteiro maior com o recuo feito, não fica na marca de 90 ° e sim na marca
dos 82°30’,
O menor ponteiro com o recuo feito, voltou para a marca dos 60°, pois voltou à
marcação 2 do mostrador. e aí vemos claramente o papel exercido pela fórmula ,que
será,
30°.h – 5,5.m = 30°.2 -5,5.15 = 60° - 82,5° = -22°30’
Que representa em módulo justamente o ângulo entre os ponteiros do relógio,
pois é justamente a diferença entre os trajetos dos arcos percorridos pelos 2 ponteiros.
Daí, Resposta: O ângulo formado pelos ponteiros do relógio que marca 2h15m é de
22°30’.
Observação: Se a pergunta fosse que horas seriam quando os ponteiros tornarem-se
coincidentes entre 2h e 3h ?
Nesse caso seria muito fácil pois o ângulo entre os ponteiros coincidentes é de 0°, daí,
0° = 30°.3 – 5,5.m e então, 5,5m = 90°
m = 90/5,5=900/55=180/11=16,363636...
Resposta: 3h 16m 21,(81) s
FIM
3