Solução gráfica de equações e inequações - Imecc

Propaganda

Roteiro da aula
MA091 – Matemática básica
Aula 19 – Solução de equações e inequações no plano.
1
Solução gráfica de equações
Francisco A. M. Gomes
2
Solução gráfica de inequações
3
Exercı́cios
UNICAMP - IMECC
Abril de 2017
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
1 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Solução gráfica de equações
2 / 21
Solução gráfica de equações
Solução gráfica de uma equação linear
Solução gráfica de uma equação linear
Aluguel de um carro
Para alugar um carro por dois dias, paga-se R$ 80,00 de taxa fixa e R$
0,75 por quilômetro rodado. Que distância pode ser percorrida com
exatos R$ 185,00?
1
Abril de 2017
2
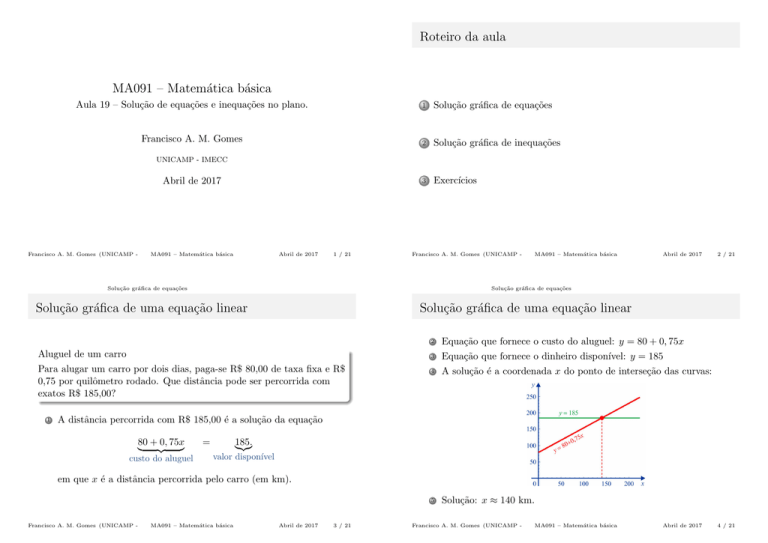
Equação que fornece o custo do aluguel: y = 80 + 0, 75x
3
Equação que fornece o dinheiro disponı́vel: y = 185
4
A solução é a coordenada x do ponto de interseção das curvas:
5
Solução: x ≈ 140 km.
A distância percorrida com R$ 185,00 é a solução da equação
80 + 0, 75x
| {z }
custo do aluguel
=
185.
|{z}
valor disponı́vel
em que x é a distância percorrida pelo carro (em km).
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
3 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
4 / 21
Solução gráfica de equações
Solução gráfica de equações
Solução alternativa
Solução alternativa
2
Equação auxiliar
y = 0, 75x − 105
Aluguel de um carro
Para alugar um carro por dois dias, paga-se R$ 80,00 de taxa fixa e R$
0,75 por quilômetro rodado. Que distância pode ser percorrida com
exatos R$ 185,00?
1
3
A solução do problema é a coordenada x do ponto em que y = 0
(intercepto-x da equação)
4
Solução: x ≈ 140 km.
Equação alternativa
80 + 0, 75x − 185 = 0
⇒
0, 75x − 105 = 0
(A diferença entre o que a locadora cobra e o dinheiro disponı́vel
deve ser zero)
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
5 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Solução gráfica de equações
Abril de 2017
6 / 21
Abril de 2017
8 / 21
Solução gráfica de equações
Roteiro para a solução gráfica de equações
Solução gráfica de uma equação quadrática
Problema
Resolva graficamente a equação x2 = x + 6
Roteiro
1. Mova todos os termos para o lado esquerdo da equação.
Dada a equação A = B, em que A e B são expressões quaisquer,
escreva A − B = 0.
1
Equação equivalente:
x2 − x − 6 = 0
2. Iguale a y o termo do lado esquerdo da equação.
Escreva a equação auxiliar y = A − B.
2
Equação auxiliar:
y = x2 − x − 6
3. Trace o gráfico da equação em duas variáveis.
Trace o gráfico de y = A − B.
4. Determine os interceptos-x.
Determine os pontos em que y = 0.
3
Gráfico da equação auxiliar.
4
Interceptos-x:
x = −2 e x = 3
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
7 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Solução gráfica de inequações
Solução gráfica de inequações
Solução gráfica de uma inequação linear
Solução gráfica de uma inequação linear
Lâmpada mais econômica
O custo de aquisição e uso de uma lâmpada incandescente é dado
por 2, 50 + 4, 8t, em que t é o tempo de uso, em meses.
2
Equação do custo da lâmpada incandescente: y1 = 2, 50+4, 8t
3
Equação do custo da lâmpada fluorescente: y2 = 14, 50 + 1, 2t
4
A lâmpada fluorescente é mais econômica quando y2 ≤ y1
5
Solução: t ≥ 3, 33 meses.
Já o custo associado a uma lâmpada fluorescente é dado por
14, 50 + 1, 2t.
Em que situação a lâmpada fluorescente é mais econômica?
1
A lâmpada fluorescente é mais econômica quando
14, 5 + 1, 2t ≤ 2, 5 + 4, 8t,
|
| {z }
{z
}
custo da
lâmpada
fluorescente
custo da
lâmpada
incandescente
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
9 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Solução gráfica de inequações
Abril de 2017
12 / 21
Solução alternativa
Lâmpada mais econômica
O custo de aquisição e uso de uma lâmpada incandescente é dado
por 2, 50 + 4, 8t, em que t é o tempo de uso, em meses.
Já o custo associado a uma lâmpada fluorescente é dado por
14, 50 + 1, 2t.
2
Equação auxiliar:
y = 12 − 3, 6t
3
A solução é o conjunto
de valores de t para os
quais y ≤ 0 (pontos
abaixo do eixo
horizontal)
4
Solução: t ≥ 3, 33
meses.
Em que situação a lâmpada fluorescente é mais econômica?
Inequação alternativa
14, 5 + 1, 2t ≤ 2, 5 + 4, 8t
10 / 21
Solução gráfica de inequações
Solução alternativa
1
Abril de 2017
⇒
12 − 3, 6t ≤ 0
(A diferença entre o custo da lâmpada fluorescente e o custo da
lâmpada incandescente deve ser menor ou igual a zero)
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
11 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Solução gráfica de inequações
Solução gráfica de inequações
Roteiro para a solução gráfica de inequações
Solução gráfica de uma inequação quadrática
Problema
Roteiro
1. Mova todos os termos para o lado esquerdo da inequação.
Dada a inequação A ≤ B (ou A ≥ B), em que A e B são expressões
quaisquer, escreva A − B ≤ 0 (ou A − B ≥ 0)
2. Iguale a y o termo do lado esquerdo da inequação.
Escreva a equação auxiliar y = A − B.
Resolva graficamente a inequação 4x2 − 8x ≥ 21
1
Inequação equivalente:
4x2 − 8x − 21 ≥ 0
2
Equação auxiliar:
y = 4x2 − 8x − 21
3. Trace o gráfico da equação em duas variáveis.
Trace o gráfico de y = A − B.
4. Determine os pontos que satisfazem a inequação.
Determine os pontos em que y ≤ 0 (ou y ≥ 0)
3
Gráfico da equação auxiliar.
4
y ≥ 0 para
x≤−
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
13 / 21
3
7
ou x ≥
2
2
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Solução gráfica de inequações
Abril de 2017
14 / 21
Exercı́cios
Exercı́cio 1
Solução gráfica de uma inequação quadrática
Problema
Resolva graficamente a inequação −x2 + 5x + 6 ≥ 0
1
Problema
Se um carro partir do quilômetro 25 de uma estrada, e viajar a uma
velocidade constante de 60 km/h, a sua posição na estrada (ou seja, o
quilômetro no qual o carro se encontra) no instante t (em horas) será
dada pela expressão 60t + 25. Determine, graficamente, o tempo que o
carro gastará para chegar ao quilômetro 175 da referida estrada.
Equação auxiliar:
y = −x2 + 5x + 6
2
Gráfico da equação auxiliar.
3
y ≥ 0 para
t = 2, 5 horas
−1 ≤ x ≤ 6
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
15 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
16 / 21
Exercı́cios
Exercı́cios
Exercı́cio 2
Exercı́cio 3
Equação quadrática
Resolva a equação
Equação quadrática
Resolva graficamente a equação
2
x =x+2
traçando os gráficos de
2x2 + 12x = 0.
y1 = x2 e y2 = x + 2.
x = −6 e x = 0
x = −1 e x = 2
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
17 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Exercı́cios
18 / 21
Exercı́cios
Exercı́cio 4
Exercı́cio 5
Problema
João resolveu assinar um plano pré-pago de telefonia móvel com
base no custo de roaming.
Para cada telefonema interurbano efetuado, a companhia A cobra
R$ 2,40 para completar a chamada, além de outros R$ 1,50 por
minuto de ligação.
Por sua vez, a companhia B cobra uma taxa fixa de R$ 1,20, ao
que se deve adicionar R$ 1,80 por minuto de conversa.
Determine graficamente para que duração de chamada interurbana
o plano B é mais barato.
Abril de 2017
Problema
Após a administração de um comprimido de Formosex, a concentração
do medicamento no plasma sanguı́neo do paciente (em mg/ml) varia de
acordo com a fórmula
t2
+ 12t
−
2
em que t é o tempo (em horas) transcorrido desde a ingestão do
comprimido. Determine graficamente o perı́odo de tempo no qual a
concentração plasmática é maior ou igual a 64 mg/ml.
t entre 8 e 16 horas
O plano da companhia B é mais vantajoso para ligações de
menos de 4 minutos.
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
19 / 21
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
20 / 21
Exercı́cios
Exercı́cio 6
Equação quadrática
Resolva graficamente a inequação
x2 + 2x ≤ −1.
x = −1
Francisco A. M. Gomes (UNICAMP - IMECC)
MA091 – Matemática básica
Abril de 2017
21 / 21