E aí, lembra-se das classificações dos triângulos?

Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
E aí, lembra-se das classificações dos triângulos?
E lembra-se das peculiaridades como a soma dos ângulos internos?
E congruência de triângulos, lembra o que é?
Se não lembrar, não tem problema, e se lembrar, aproveite e revise junto.
Triângulos Revisão: Conceito e Classificação
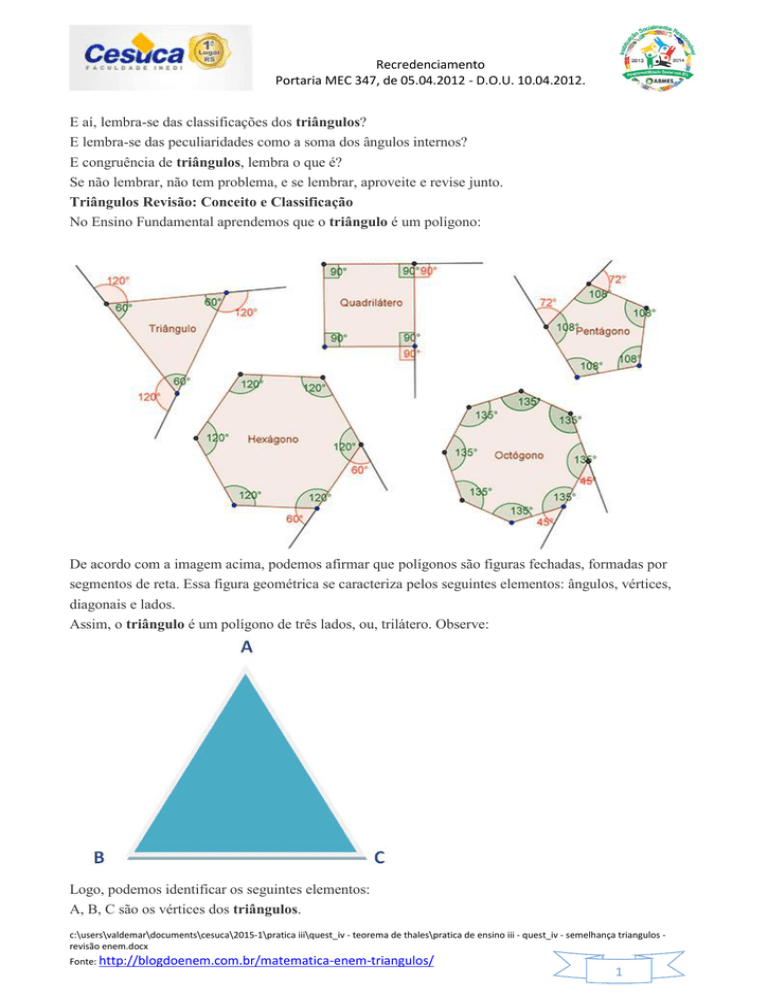
No Ensino Fundamental aprendemos que o triângulo é um polígono:
De acordo com a imagem acima, podemos afirmar que polígonos são figuras fechadas, formadas por
segmentos de reta. Essa figura geométrica se caracteriza pelos seguintes elementos: ângulos, vértices,
diagonais e lados.
Assim, o triângulo é um polígono de três lados, ou, trilátero. Observe:
Logo, podemos identificar os seguintes elementos:
A, B, C são os vértices dos triângulos.
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_iv - teorema de thales\pratica de ensino iii - quest_iv - semelhança triangulos revisão enem.docx
Fonte: http://blogdoenem.com.br/matematica-enem-triangulos/
1
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Os lados dos triângulos são simbolizados pelos vértices, que nada mais são do que o ponto de encontro
(AB, BC,AC) dos segmentos de retas.
Cada lado do triângulo representa um ângulo, logo, tendo três lados, possui três ângulos.
Tipos de triângulo
Um triângulo é classificado de acordo com a medida de cada um dos seus lados, ou seja, de cada um dos
seus ângulos. Vejamos:
Triângulo Escaleno: todos os lados são diferentes.
Triângulo isósceles: dois lados iguais e os ângulos opostos a esses lados iguais.
Triângulo equilátero: todos os lados e ângulos são iguais. Concluímos que seus ângulos serão de 60°.
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_iv - teorema de thales\pratica de ensino iii - quest_iv - semelhança triangulos revisão enem.docx
Fonte: http://blogdoenem.com.br/matematica-enem-triangulos/
2
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Obs.: os triângulos também podem ser classificados quanto ao ângulo.
Triângulo retângulo: tem um ângulo que mede 90º.
Obtusângulo: tem um ângulo maior que 90°.
Acutângulo: Todos os ângulos são menores de noventa graus.
Triângulos Congruentes
Antes de falar sobre os critérios de congruência de um triângulo, vou pedir pra você assistir à videoaula
do professor Nerckie. O vídeo tem 15min e está disponível no canal aberto do Youtube, dá uma olhada:
Dois triângulos são denominados congruentes quando possuem a mesma medida nos três lados e nos três
ângulos.
Exemplo: Os triângulos ABC e A’B’C’ são congruentes:
Em dois triângulos congruentes, são congruentes entre si:
a) os lados opostos a ângulos congruentes;
b) os ângulos opostos a lados congruentes;
Existem cinco critérios de congruência entre triângulos. Esse assunto é mais aprofundado no ensino
superior, mas ainda assim é cobrado na prova de Matemática do Enem. Mas o foco do seu estudo deve
estar na semelhança entre os triângulos.
Dica 3: entenda operações envolvendo cálculo de juros http://blogdoenem.com.br/matematicaenem-calculo-juros/
Semelhança entre triângulos
Para descobrir se dois triângulos são semelhantes, você precisa entender o conceito de congruência. Dois
triângulos são semelhantes quando seus ângulos são respectivamente congruentes ou os lados
correspondentes são proporcionais.
Obs.: Trata-se de conceito de proporcionalidade – Razão e Proporção.
Razão de semelhança
A razão de semelhança de dois triângulos é uma medida de proporcionalidade entre eles e é dada por uma
constante: D/A = E/B = F/C = k.
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_iv - teorema de thales\pratica de ensino iii - quest_iv - semelhança triangulos revisão enem.docx
Fonte: http://blogdoenem.com.br/matematica-enem-triangulos/
3
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
Para entender todos esses conceitos, nada melhor do que praticar não é mesmo? Acompanhe a resolução
do exercício a seguir.
1) Considerando os triângulos MNP e PQR da figura abaixo, podemos afirmar que ∆MNP ~ ∆PQR.
Como você justifica essa afirmação?
2) Considerando a figura na qual C≈ F e B≈E, determine as medidas x e y nela indicadas.
Resolução:
∆ DFE ≈ ∆ ACB
AB = AC = CB → 14 = 10 → 70 = 10x → x =7
DE DF FE
x
5
x=7, logo, y = 14-x, logo:
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_iv - teorema de thales\pratica de ensino iii - quest_iv - semelhança triangulos revisão enem.docx
Fonte: http://blogdoenem.com.br/matematica-enem-triangulos/
4
Recredenciamento
Portaria MEC 347, de 05.04.2012 - D.O.U. 10.04.2012.
y = 14 – x
y=7
2
Então x=7 e y = 3,5
Questão do ENEM 2009
(Enem/2009) A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um
paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8
metro.
A distância, em metros, que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é
A) 1,16 metros
B) 3,0 metros
C) 5,4 metros
D) 5,6 metros
E) 7,04 metros
Resolução: Resposta D
Como você pode observar não é tão difícil. Espero que as dicas ajudem você a gabaritar a prova
de Matemática doEnem. Bons estudos e boa sorte!
Este post foi produzido por Leonardo Ferreira. Ele atuou como professor de Matemática em
projetos sociais. Em sua trajetória, foi aprovado em Matemática-UERJ e Ciências Contábeis-UFF,
mas optou pela bolsa integral do PROUNI para o curso de Ciência Contábeis da Cândido Mendes
através do ENEM. Pretende cursar o mestrado para se dedicar a uma das suas maiores paixões:
dar aulas. https://www.facebook.com/leonferreira.br?fref=ts
c:\users\valdemar\documents\cesuca\2015-1\pratica iii\quest_iv - teorema de thales\pratica de ensino iii - quest_iv - semelhança triangulos revisão enem.docx
Fonte: http://blogdoenem.com.br/matematica-enem-triangulos/
5