01 - Colégio Anchieta

COLÉGIO ANCHIETA-BA _ 2005
2ª AVALIAÇÃO DE MATEMÁTICA _ UNIDADE IV
ELABORAÇÃO: PROF. OCTAMAR MARQUES.
RESOLUÇÃO: PROFA. MARIA ANTÔNIA GOUVEIA.
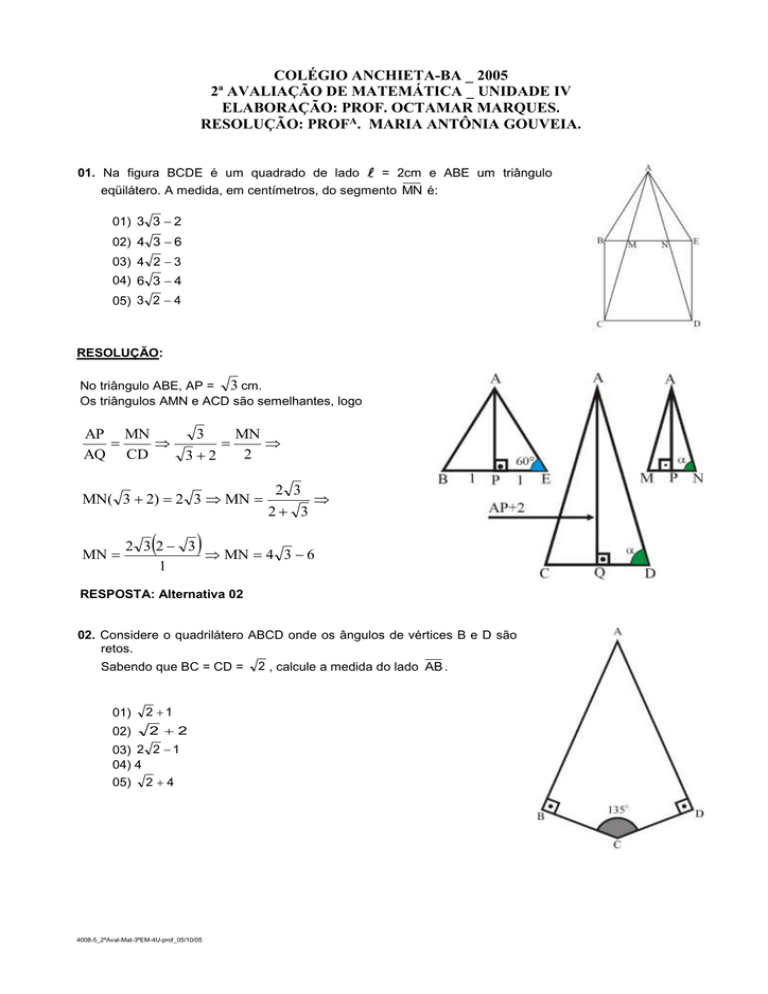
01. Na figura BCDE é um quadrado de lado  = 2cm e ABE um triângulo
eqüilátero. A medida, em centímetros, do segmento MN é:
01) 3 3  2
02) 4 3  6
03) 4 2  3
04) 6 3  4
05) 3 2  4
RESOLUÇÃO:
No triângulo ABE, AP = 3 cm.
Os triângulos AMN e ACD são semelhantes, logo
AP MN
3
MN




AQ CD
2
32
MN( 3  2)  2 3  MN 
MN 

2 3
2 3


2 3 2 3
 MN  4 3  6
1
RESPOSTA: Alternativa 02
02. Considere o quadrilátero ABCD onde os ângulos de vértices B e D são
retos.
Sabendo que BC = CD =
01)
2 1
02)
2 2
03) 2 2  1
04) 4
05) 2  4
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
2 , calcule a medida do lado AB .

RESOLUÇÃO:
Sabemos que tg 2 =
2tgα
.
1  tg 2 α
 135 
2tg 

 2 
Fazendo 2 = 135° temos: tg135° =
 135 
1  tg 2 

 2 
 135 
2tg 

2 

Sendo tg135° = – tg45° = – 1 
=–1
2  135 
1  tg 

 2 
 135 
2  135 
2tg 
  1  tg 

 2 
 2 
 135 
 135 
tg 2 
  2tg 
 1  0 
 2 
 2 
 135  2  4  4 2  2 2
tg 

 1 2

2
2
 2 
AB
 135  AB
 1 2 
 AB  2  2

2
 2  BC
No triângulo retângulo ABC, tg 
RESPOSTA: Alternativa 02.
03. Na figura vemos o setor circular ABC de raio x e comprimento do arco BC
igual a y.
Sabendo que seu perímetro é igual a 12cm calcule em centímetros
quadrados, a área máxima desse setor.
Nota: A área de um setor circular é igual ao semiproduto do raio pelo
comprimento do arco.
01) 30
2) 5
03) 7
04) 8
RESOLUÇÃO:
2x  y  12
 y  12  2x


2
 

xy
x(12  2x)  S   x  6x
S  2
S 
2
Sendo S = – x2 + 6x , o valor máximo de S =
  - 36

9
4a
-4
RESPOSTA: Alternativa 05.
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
2
05) 9

04.
Calcule o volume de uma pirâmide triangular regular de aresta lateral igual a 8u.c. e aresta da base igual
a 6u.c.
01) 6 39 u.v.
02) 3 39 u.v.
03) 6 15 u.v.
04) 4 15 u.v.
05) 4 33 u.v.
RESOLUÇÃO:
O volume de uma pirâmide é calculado através da fórmula
V=
Sbase  h
.
3
A altura desta pirâmide é o cateto VH do triângulo
retângulo VHC, logo. VH 
 
82  2 3
2
 52  2 13
36 3
 2 13
18 39
4
Assim: V =

 6 39 ..
3
3
RESPOSTA: Alternativa 01.
05. Sejam A e B subconjuntos do universo U.
Sabendo que n(U) = 19, n(A) = 7, n(B) = 11 e n[(AB) – (A  B)] =10 calcule n A  B

01) 1
02) 2
03) 3
04) 4

05) 5
RESOLUÇÃO:
Os números colocados nas diversas regiões do diagrama refere-se à quantidade de elementos de cada
subconjunto representado pela região em que foi escrito:
n[(AB) – (A  B)] =10  7 – x + 11 – x = 10 
2x = 8  x = 4.
Sendo n(U) = 19  7 – x + 11 – x + x + y = 19 
– x + y = 1  – 4 + y = 1  y = 5.




Como n A  B = y  n A  B = 5.
RESPOSTA: Alternativa 05.
06.

2x  5, se - 1  x  0
Determine a imagem da função f tal que f(x) =  2

x  4x  5, se 0  x  4
01) [0,5]
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
02) [1,5]
03) [– 1,5]
3
04) [– 3,5]
05) [0,5] – {3}

RESOLUÇÃO:
Analisando o gráfico concluímos que a imagem da
função f é o intervalo [1,5].
y
5
RESPOSTA: Alternativa 02.
3
1
-1
07.
2
4
x
Sendo f(x+1) = 2x + 1,  x R, determine k de modo que (f o f)– 1 (k – 1) = k
01) k = 1
02) k = – 1
03) k =
2
3
04) k =
3
2
05) k =
1
2
RESOLUÇÃO:
Sendo f(x+1) = 2x + 1,  x R  f(x) = 2(x– 1) + 1  f(x) = 2x – 1,  x R.  (f o f)(x) = 2(2x – 1) – 1 = 4x – 3 
(f o f)– 1(x) =
x3
k 1 3
2
 k  k  2  4k  k  .
 se (f o f)– 1 (k – 1) = k, temos
4
4
3
RESPOSTA: Alternativa 03.
08.
Quantos inteiros pertencem ao domínio da função y =
01) 9
02) 8
03) 7
04) 6
x 2  7x  6
 x 2  2x  3
?
05) 5
RESOLUÇÃO:
A expressão y =
x 2  7x  6
 x 2  2x  3
representa um número real para os valores de x que satisfazem à
desigualdade:
x 2  7x  6
0.
 x 2  2x  3
As raízes de x2+7x +6 são os números – 1 e – 6 ; e as raízes de – x2+2x + 3 são os números – 1 e 3..
Fazendo o estudo da variação do sinal da fração do primeiro membro de
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
4
x 2  7x  6
0:
 x 2  2x  3

Logo a inequação é satisfeita no conjunto [– 6, 3[ – { – 1, 3} ao qual pertencem os números inteiros: –6, 5,
–4, –3, –2, 0, 1 e 2. Então ao todo temos 8 números inteiros.
RESPOSTA: Alternativa 02.
09.
 x 2  4x

 7x
O número de soluções inteiras do sistema  x  2
3x  9  0

01) uma
02) duas
03) três
04) quatro
05) uma infinidade
RESOLUÇÃO:
 x 2  4x
 x 2  4x - 7x 2  14x
 - 6x 2  18x
 7x
0 
0



 x2
x2
 x2
3x  9  0
x  3
x  3



- 6x 2  18x
Resolvendo a inequação
0:
x2
Raízes de -6x2 + 18x: 0 e 3.
Raíz de x – 2 : 2.
 - 6x 2  18x
0  x  2 ou x  3
0

 
 x2
x  3
x  3

Existe apenas uma solução inteira pertencente ao
intervalo ]0,2[ que é o 1.
RESPOSTA: Alternativa 01.
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
5

10.
Calcule a soma dos múltiplos de 7 que estão compreendidos entre os números 75 e 249.
01) 3021
02) 3215
03) 4025
04) 4095
05) 5025
RESOLUÇÃO:
Se 75 < 7x < 249, então o menor valor para 7x é 77 e o maior valor é 245.
Assim temos a P.A. : 77, 84, 91, ..., 245.
Pela relação do termo geral de uma P.A., 77 + 7(n – 1) = 245  11 + n – 1 = 35  n = 25.
A soma dos termos de uma P.A. é dada por Sn =
a 1  a n n
 S25 =
2
77  24525  4025
2
RESPOSTA: Alternativa 03.
10
11.
x
Qual dos números a seguir é solução da equação
n
 2(x 11  1) ?
n 0
01)
2
3
02)
3
2
03) 1
04)
1
2
05) 0
RESOLUÇÃO:
Os termos da seqüência são: x0, x1, x2, ....., x10 que é uma P.G. com o primeiro termo igual a 1, razão x e
número de termos 11.
a 1 (q n  1)
Sendo Sn =
, então
q 1
3
x= .
2
1
1(x 11  1)
1(x 11  1)
11
 2  2x – 2 = 1 
x =

= 2(x  1) 

x 1
x 1
x 1
n 0
10
n
Resposta: Alternativa 02.
12.
Quantos são os anagramas da palavra “PETECA” que começam com vogal?
01) 240
02) 180
03) 120
04) 60
05) 360
RESOLUÇÃO:
E
A
E
P
T
5! = 120
C
A
E
P
5! 120

 60
2!
2
São (120 + 60) = 180 anagramas.
Resposta: Alternativa 02.
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
E
6
T
C

13.
1 1 
 e B =
Considere a equação matricial AX– 1 = B, onde A = 
1 2 
Determine a soma dos elementos da matriz X.
01) 1
02)
7
2
03)
3
2
5
2
04)
05) – 1
RESOLUÇÃO:
AX– 1 = B  A – 1 AX– 1 = A – 1 B  X– 1 = A – 1 B  X = B – 1A
 2 0


 1
 1 1  1 1 


 .  X =  1
X=

2
1 2 
 2
A soma dos termos de X é
0  1 1
1  . 
 X =
 1 2 
2
1 1 

1.
0

2

1
5
+1+1 = .
2
2
Resposta: Alternativa 04.
14. Na figura ABC é um triângulo eqüilátero de lado  = 4.
Determine a equação da reta que possui o vértice C e é
perpendicular à reta suporte do lado
01)
AC
3x  y  2  0
02) x  3 y  1  0
03) 3 x  2 3 y  8  0
04)
3 x  3y  8 3  0
05) x  3 y  4  0
RESOLUÇÃO:
Se o lado do triângulo eqüilátero ABC mede 4, então a sua
altura CH =
4 3
 2 3  C = (2,2 3 ).
2
O coeficiente da reta AC que determina com o eixo das
3 , logo o
abscissas um ângulo de 60o é tg 60o =
coeficiente angular da reta r
 AC é igual a 
A equação de r tem então a forma y = 
Como r passa pelo ponto C:
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05

1
3

3
.
3
3
x+b.
3
3
.2+b = 2 3 
3
7
1 0 

 .
1 2 

2 3 8 3
=

3
3
b =2
3 +
y= 
3 8 3
x+
 3y +
3
3
3 x-8 3 = 0.
Resposta: Alternativa 04.
15.
Um objeto foi vendido por R$72,00 com um lucro de 20% sobre o preço de custo.
Se esse objeto fosse vendido por R$90,00 qual seria o lucro percentual relativo ao custo?
01) 50%
02) 60%
03) 40%
04) 45%
05) 65%
RESOLUÇÃO:
Como o objeto foi vendido por R$72,00 com um lucro de 20% sobre o preço de custo, então 1,2C = 72 
C=
72
 60 .
1,2
Como o custo foi de R$60,00, se esse objeto fosse vendido por R$90,00 o lucro seria de R$30,00.
Logo o lucro percentual relativo ao custo seria
30
 50% .
60
Resposta: Alternativa 01.
16. 24 alunos participaram de uma prova. O número de
alunos que tiveram determinada nota foi representado pelo
diagrama de setores, ao lado, onde m(AÔC) = 90o e m(BÔC)
= 120o.
Calcule o desvio padrão dessa distribuição utilizando apenas
a parte inteira da média aritmética das notas.
01) 1,2
02) 1,7
03) 1,9
04) 2,0
05) 2,4
RESOLUÇÃO:
Sendo m(AÔC) =
90o,
90 o
 24  6 .
então a quantidade de alunos com nota 8 é
360 o
Sendo m(BÔC) = 120o, então a quantidade de alunos com nota 4 é
120 o
 24  8 .
360 o
O número de alunos com nota 2 é então 10.
A média da turma foi de
6  8  8  4  10  2 48  32  20 100


 4,166...
24
24
24
O desvio padrão dessa distribuição utilizando apenas a parte inteira da média aritmética das notas é
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
8


68  4  84  4  102  4
96  40
136


 5,666...  2,38... .
24
24
24
2
2
2
Resposta: Alternativa 05.
QUESTÃO DISCURSIVA
Determine r de modo que os coeficientes de xr e xr+1 no desenvolvimento de (3x+2)19 sejam iguais.
RESOLUÇÃO:
O termo geral do desenvolvimento de (3x+2)19 é
p
3x 
Tp 1  C19
19  p
19- r 19 19  r
Fazendo 19 – p = r  p = 19 – r  T(19 - r) 1 = C19 3
p 19  p p 19  p
3 .2 .x .
.2p = C19
- r r 19- r r
.219- r.x1919 r  C19
.x .
19 3 .2
.
18- r 19 18 r
Fazendo 19 – p = r + 1  p = 18 – r  T(18 r) 1 = C19 3
- r 1 r 18- r 1 r
.218- r.x1918 r  C18
.x .
19 3 .2
Sendo os coeficientes dos dois resultados iguais:
- r r 19- r
18- r 1 r 18- r
C19
= C19 3 .2

19 3 .2
19!.3r.219 r
19!.31 r.218 r


(19  r)!.r! (18  r)!.1  r !
19! 3r.219 r
19! 31 r.218 r
.

(19  r) (18  r)! r! (18  r)! 1  r  r!
Multiplicando os dois membros por
(18  r)! r!
19! 3r.218r
19! 3r.219 r
(18  r)! r!
19! 31 r.218 r
(18  r)! r!




r 18 r
(19  r) (18  r)! r! 19! 3 .2
(18  r)! 1  r  r! 19! 3r.218 r
2
3

 2  2r  57 - 3r  r  11 .
(19  r) (1  r)
Resposta: 11
4008-5_2ªAval-Mat-3ªEM-4U-prof_05/10/05
9