Baixar o arquivo - Matemática

AGRUPAMENTO DE ESCOLAS D. JOSÉ I - VRSA – MATEMÁTICA 6.º ANO – 2014/15
Ficha A4 – Revisão
NOME _______________________________________________________ N.º ___ Turma_____
NOME_________________________________________________________________
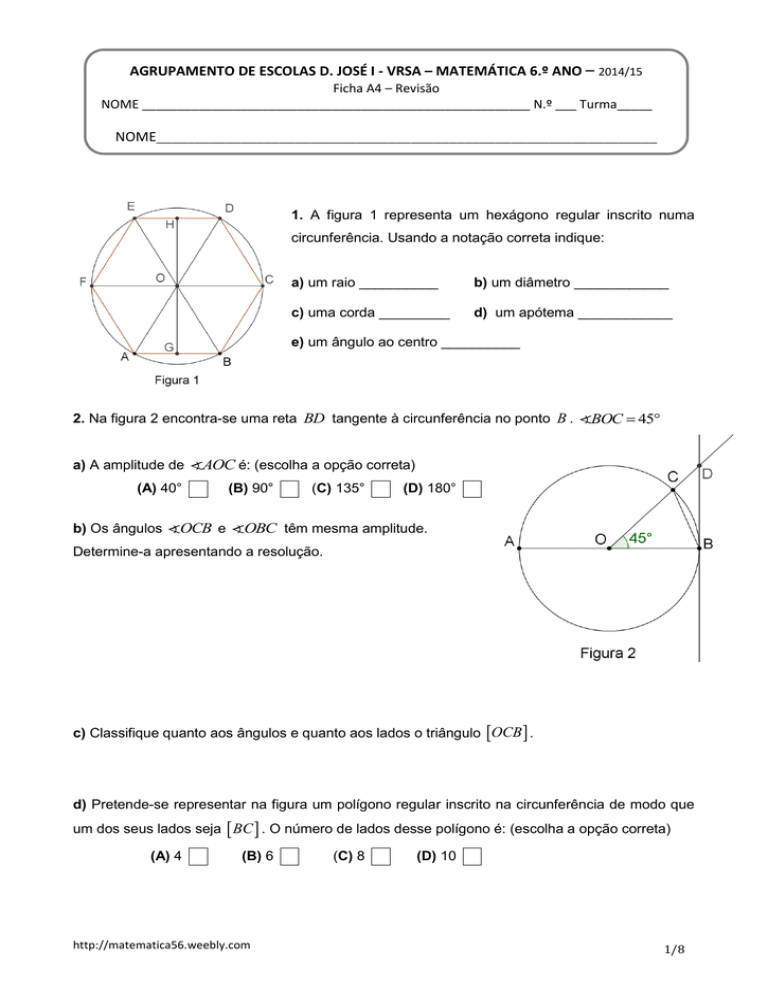
1. A figura 1 representa um hexágono regular inscrito numa
circunferência. Usando a notação correta indique:
a) um raio __________
b) um diâmetro ____________
c) uma corda _________
d) um apótema ____________
e) um ângulo ao centro __________
2. Na figura 2 encontra-se uma reta BD tangente à circunferência no ponto B .
a) A amplitude de
AOC é: (escolha a opção correta)
(A) 40°
b) Os ângulos
BOC  45
OCB e
(B) 90°
(C) 135°
(D) 180°
OBC têm mesma amplitude.
Determine-a apresentando a resolução.
c) Classifique quanto aos ângulos e quanto aos lados o triângulo OCB  .
d) Pretende-se representar na figura um polígono regular inscrito na circunferência de modo que
um dos seus lados seja  BC  . O número de lados desse polígono é: (escolha a opção correta)
(A) 4
(B) 6
http://matematica56.weebly.com
(C) 8
(D) 10
1/8
3. A figura 3 apresenta uma sequência de hexágonos regulares geometricamente iguais.
Considere que a medida dos lados dos hexágonos vale 1 unidade. Suponha também que a
sequência continua seguindo o mesmo padrão, isto é, a cada figura acrescenta-se um hexágono,
coincidindo dois lados de dois hexágonos.
A tabela seguinte relaciona o número de hexágonos com o perímetro da figura.
Número de hexágonos
1
2
Perímetro da figura
6
10
3
4
5
a) Complete a tabela.
b) Escreva uma lei de formação da sequência.
c) Escreva uma expressão geradora da sequência.
d) Utilize a expressão geradora para determinar o perímetro de uma figura com 500 hexágonos.
(Se não determinou a expressão geradora use a expressão
2n  1 )
e) Verifique se o número de hexágonos e o perímetro das figuras são ou não grandezas
diretamente proporcionais. Apresente a resolução.
http://matematica56.weebly.com
2/8
4. O António tinha 120 berlindes e resolveu dar alguns aos seus dois primos.
Deu
1
dos berlindes a um primo e ao outro 35% (dos 120 ).
3
Com quantos berlindes ficou o António? Apresente a resolução.
5. Numa loja de desporto oferecem carteiras de cromos aos clientes que comprem camisolas.
Por cada 2 camisolas, 5 carteiras de cromos. Uma família comprou várias camisolas e recebeu 30
carteiras de cromos. Quantas camisolas comprou? Apresente a resolução.
6. O mapa representa parte do Algarve, à escala de 1/750000.
Utilizando uma régua, faça as medições necessárias para determinar a distância, em quilômetros,
http://matematica56.weebly.com
3/8
3
2
7. Considere os números A  2  3  5 e B  190
a) Utilizando a decomposição apresentada indique 3 divisores de A que não sejam números
primos.
b) Decomponha B em fatores primos e use essa decomposição para determinar m. d . c.( A, B )
8. De uma estação partem comboios num sentido de 50 em 50 minutos e no outro sentido de 35
em 35 minutos, com início às 9h da manhã.
A que horas voltam a partir dois comboios em simultâneo? Mostre como chegou ao resultado.
9. Calcule o valor expressão e apresente o resultado em forma de fração irredutível.
Apresente os cálculos.
 1 1
23     : 3
 2 3
http://matematica56.weebly.com
4/8
Resolução
1. A figura 1 representa um hexágono regular inscrito numa
circunferência. Usando a notação correta indique:
a) um raio
OC 
b) um diâmetro  AD 
c) uma corda CD 
d) um apótema OH 
e) um ângulo ao centro
COD
Nota: Há várias respostas possíveis
2. Na figura 2 encontra-se uma reta BD tangente à circunferência no ponto B .
a) A amplitude de
AOC é: (escolha a opção correta)
(A) 40°
b) Os ângulos
BOC  45
OCB e
(B) 90°
(C) 135° x
(D) 180°
OBC têm mesma amplitude.
Determine-a apresentando a resolução.
OCB  OCB  45  180º
OCB  OCB  180º 45
OCB  OCB  135
Porque são ângulos internos de um
triângulo
Então cada ângulo mede 135 : 2  67,5
c) Classifique quanto aos ângulos e quanto aos lados o triângulo OCB  .
Triângulo acutângulo isósceles.
d) Pretende-se representar na figura um polígono regular inscrito na circunferência de modo que
um dos seus lados seja  BC  . O número de lados desse polígono é: (escolha a opção correta)
(A) 4
(B) 6
http://matematica56.weebly.com
(C) 8 x
(D) 10
5/8
3. A figura 3 apresenta uma sequência de hexágonos regulares geometricamente iguais.
Considere que a medida dos lados dos hexágonos vale 1 unidade. Suponha também que a
sequência continua seguindo o mesmo padrão, isto é, a cada figura acrescenta-se um hexágono,
coincidindo dois lados de dois hexágonos.
A tabela seguinte relaciona o número de hexágonos com o perímetro da figura.
Número de hexágonos
1
2
3
4
5
Perímetro da figura
6
10
14
18
22
a) Complete a tabela.
b) Escreva uma lei de formação da sequência.
O primeiro termo é 6 e os seguintes são obtidos adicionando 4 unidades ao termo anterior.
c) Escreva uma expressão geradora da sequência.
4n  2
d) Utilize a expressão geradora para determinar o perímetro de uma figura com 500 hexágonos.
(Se não determinou a expressão geradora use a expressão
2n  1 )
4  500  2  2000  2  2002
e) Verifique se o número de hexágonos e o perímetro das figuras são ou não grandezas
diretamente proporcionais. Apresente a resolução.
6 12
 , logo as grandezas não são diretamente proporcionais.
1 2
http://matematica56.weebly.com
6/8
4. O António tinha 120 berlindes e resolveu dar alguns aos seus dois primos.
Deu
1
dos berlindes a um primo e ao outro 35% (dos 120 ).
3
Com quantos berlindes ficou o António? Apresente a resolução.
Deu a um primo
1
1
120
 40 berlindes
de 120 , isto é,  120 
3
3
3
Deu ao outro primo 35% de 120 , isto é, 0,35  120  42 berlindes
Ficou com 120   40  42   120  82  38 berlindes
O António ficou com 38 berlindes.
5. Numa loja de desporto oferecem carteiras de cromos aos clientes que comprem camisolas.
Por cada 2 camisolas, 5 carteiras de cromos. Uma família comprou várias camisolas e recebeu 30
carteiras de cromos. Quantas camisolas comprou? Apresente a resolução.
2 x

,
5 30
x
2  30 60

 12
5
5
A família comprou 12 camisolas.
6. O mapa representa parte do Algarve, à escala de 1/750000.
Utilizando uma régua, faça as medições necessárias para determinar a distância, em quilómetros,
de Vila Real de Santo António a Faro. Mostre como chegou ao resultado.
de Vila Real de Santo António a Faro. Mostre como chegou ao resultado.
(Supõe-se que na impressão a distância é 7 cm)
Então 7cm  750000  5250000cm  52,5km
A distância entre as cidades é 52,5 km.
http://matematica56.weebly.com
7/8
3
2
7. Considere os números A  2  3  5 e B  190
a) Utilizando a decomposição apresentada indique 3 divisores de A que não sejam números
primos.
4,6 e 15 (Por exemplo)
b) Decomponha B em fatores primos e use essa decomposição para determinar m. d . c.( A, B )
190  2  5 19
m. d . c.( A, B )  2  5  10
8. De uma estação partem comboios num sentido de 50 em 50 minutos e no outro sentido de 35
em 35 minutos, com início às 9h da manhã.
A que horas voltam a partir dois comboios em simultâneo? Mostre como chegou ao resultado.
Vamos determinar m.m.c.  35,50 
50  2  52 ,
35  5  7
m.m.c.  35,50  2  52  7  350
350m  5  60m  50m  5h50m
Então os dois comboios partem em simultâneo de 5h50m em 5h50m
Partirão de novo em simultâneo às 14h50m.
9. Calcule o valor expressão e apresente o resultado em forma de fração irredutível.
Apresente os cálculos.
1
8 1 8 4
 1 1
 1  3  2 1 
23     : 3  8  

 : 3  8 : 3   
6
6 3 18 9
 2 3
 23 
http://matematica56.weebly.com
8/8