Lei de Gauss

Lei de Gauss
Origem: Wikipédia, a enciclopédia livre.
A lei de Gauss é a lei que estabelece a relação entre o fluxo de campo elétrico que passa através
de uma superfície fechada com a carga elétrica que existe dentro do volume limitado por esta
superfície. A lei de Gauss é uma das quatro Equações de Maxwell, juntamente com a lei de Gauss
do magnetismo, a lei da indução de Faraday e a lei de Ampère-Maxwell e foi elaborada por Carl
Friedrich Gauss em 1835, porém só foi publicada após 1867. Gauss foi um importante matemático
alemão que fez descobertas em teoria dos números, geometria e probabilidade, tendo também
contribuições em astronomia e na medição do tamanho e formato da Terra.
Fluxo do campo elétrico
O fluxo de campo elétrico,
, é uma grandeza escalar e pode ser considerado como uma
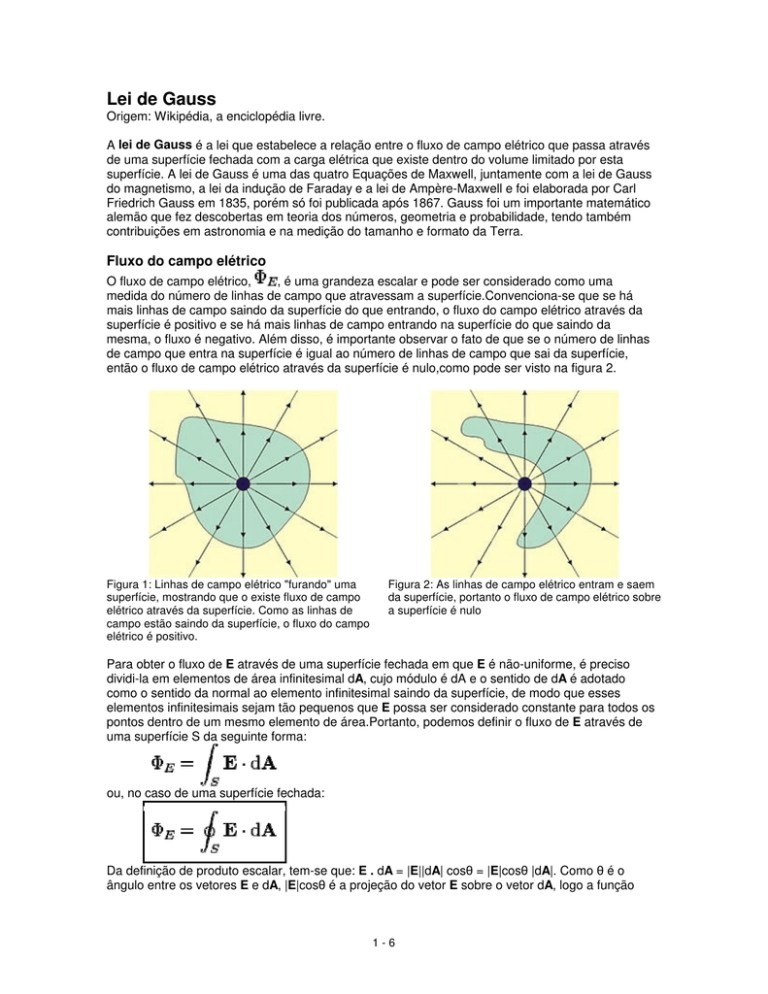
medida do número de linhas de campo que atravessam a superfície.Convenciona-se que se há
mais linhas de campo saindo da superfície do que entrando, o fluxo do campo elétrico através da
superfície é positivo e se há mais linhas de campo entrando na superfície do que saindo da
mesma, o fluxo é negativo. Além disso, é importante observar o fato de que se o número de linhas
de campo que entra na superfície é igual ao número de linhas de campo que sai da superfície,
então o fluxo de campo elétrico através da superfície é nulo,como pode ser visto na figura 2.
Figura 1: Linhas de campo elétrico "furando" uma
superfície, mostrando que o existe fluxo de campo
elétrico através da superfície. Como as linhas de
campo estão saindo da superfície, o fluxo do campo
elétrico é positivo.
Figura 2: As linhas de campo elétrico entram e saem
da superfície, portanto o fluxo de campo elétrico sobre
a superfície é nulo
Para obter o fluxo de E através de uma superfície fechada em que E é não-uniforme, é preciso
dividi-la em elementos de área infinitesimal dA, cujo módulo é dA e o sentido de dA é adotado
como o sentido da normal ao elemento infinitesimal saindo da superfície, de modo que esses
elementos infinitesimais sejam tão pequenos que E possa ser considerado constante para todos os
pontos dentro de um mesmo elemento de área.Portanto, podemos definir o fluxo de E através de
uma superfície S da seguinte forma:
ou, no caso de uma superfície fechada:
Da definição de produto escalar, tem-se que: E . dA = |E||dA| cos = |E|cos |dA|. Como é o
ângulo entre os vetores E e dA, |E|cos é a projeção do vetor E sobre o vetor dA, logo a função
1-6
desse produto escalar dentro da integral é selecionar algo proporcional à componente do campo
elétrico que está "furando" à superfície infinitesimal dA, o que é coerente com a definição de fluxo
dada anteriormente.
Por fim, se uma carga pontual estiver fora da superfície, as linhas de campo que partem da carga
pontual irão entrar e sair da superfície, visto que as linhas de campo de uma carga pontual são
radiais. Por isso, pode-se concluir que se uma carga está fora de uma superfície, então o fluxo do
campo elétrico dessa carga através da superfície é nulo, ou seja:
Lei de Gauss
A lei de Gauss estabelece uma relação entre o fluxo de campo elétrico através de uma superfície
fechada e as cargas que estão no interior dessa superfície. Algumas considerações importantes
sobre a de lei de Gauss são:
• A lei de Gauss não contém nenhuma informação que não esteja contida na lei de Coulomb
e no princípio da superposição. Inclusive, é possível obter a lei de Coulomb a partir da lei
de Gauss e vive-versa.
• É fundamental para a lei de Gauss, o fato de que a força elétrica é proporcional ao inverso
do quadrado da distância. É esse fato que faz com que o fluxo de E não dependa da
"superfície gaussiana" escolhida e dependa apenas das cargas que estão localizadas no
interior da superfície. Dessa forma, é possível pensar numa lei de Gauss que estabeleça
uma relação de fluxo para qualquer campo cuja lei de força associada a esse campo seja
proporcional ao inverso do quadrado da distância, como a força gravitacional, por exemplo,
logo existe uma lei de Gauss da gravitação.
• Apesar da lei de Coulomb nos fornecer o necessário para calcular o campo elétrico de uma
distribuição de cargas, muitas vezes, as integrais que envolvem o cálculo do campo
elétrico podem ser complicadas de serem resolvidas, mesmo para casos razoavelmente
simples. É nesse ponto que reside um dos aspectos de maior eficiência da lei de Gauss: o
cálculo do campo elétrico em distribuições de carga que possuam determinados tipos de
simetria torna-se extremamente simples.
• A lei de Gauss se refere sempre ao fluxo no interior de uma superfície gaussiana
escolhida. Portanto, para utilizar a lei de Gauss, é necessário definir o que é uma
"superfície gaussiana". Esta é, por sua vez, uma superfície arbitrariamente escolhida.
Normalmente, essa superfície é escolhida de modo que a simetria da distribuição de carga
permita, ao menos em parte da superfície, um campo elétrico de intensidade constante.
Forma integral da lei de Gauss
Figura 3: Superfície gaussiana esférica centrada em q.
2-6
Para entender como a lei de Gauss relaciona o fluxo do campo elétrico no interior de uma
superfície gaussiana com a carga no interior dessa mesma superfície, escolhe-se uma superfície
qualquer com uma carga q em seu interior, como por exemplo a superfície da figura 1. Então,
escolhe-se outra superfície gaussiana S' que está envolvendo q no interior de S. A forma dessa
superfície S' pode ser qualquer, contudo, a fim de facilitar os cálculos e a visualização, vamos fazer
dessa superfície S', uma esfera de raio r centrada na carga q, como por exemplo a superfície
gaussiana representada na figura 3. O raio r é tal que S' esteja inteiramente dentro de S. O fluxo do
campo elétrico através dessa esfera é dado por:
Como tanto E quanto dA são radiais, o produto escalar torna-se o produto dos módulos, então:
Como |E| é constante na superfície da esfera, podemos tirá-lo da integral e temos:
Portanto, é possível observar que o fluxo através da superfície S' é um número que independe do
raio da esfera. Dessa forma, o fluxo que sai da superfície S também será
. Esse é um valor
independente da forma da superfície S, desde que esta tenha uma carga q em seu interior. Se uma
carga q está no exterior da superfície S, as suas linhas de campo entram e saem da superfície S,
por isso, o fluxo de campo elétrico dessa carga sobre a superfície é nulo. Logo:
Por fim, se tivermos mais de uma carga no interior da superfície gaussiana, vale o princípio da
superposição de modo que:
Portanto, a Lei de Gauss na forma integral pode ser enunciada da seguinte forma:
Aplicações
É importante ressaltar que a lei de Gauss se torna eficiente apenas em casos em que há simetria.
[3]
Mais precisamente, nos casos nos quais existe simetria esférica, cilíndrica ou plana. Dessa
forma, contruir superfícies gaussianas que aproveitem a simetria é de vital importância para a
[2]
aplicação da lei de Gauss, visto que a eficiência da lei de Gauss consiste em utilizar a simetria
das distribuições de carga para calcular campo elétrico dessas com mais facilidade.
3-6
Campo elétrico no interior e no exterior de uma esfera
Figura 4: Duas superfícies gaussianas esféricas em torno de uma esfera uniformemente carregada de raio R.
A superfície gaussiana externa à esfera de raio R possui raio r' e a superfície gaussiana interna à esfera
possui raio r.
Para uma esfera de raio R, como mostrada na figura 4, com carga Q uniformemente distribuída
pela esfera, tem-se:
No exterior da esfera
Para se obter o campo no interior da esfera, escolhe-se, como superfície gaussiana, a superfície
esférica de raio r', situada no exterior da esfera de raio R, como mostra a figura 4. Pode-se
imaginar que, muito longe da esfera, o campo elétrico que se sente é como o campo de uma carga
puntiforme. Além disso, devido à simetria esférica, o campo elétrico deve apontar na direção radial.
Dessa forma, aplicando a lei de Gauss:
O campo deve apontar na direção radial e, portanto, E e dA possuem a mesma direção e sentido
e, por isso, segue que: E . dA = E dA. Logo:
O módulo do campo elétrico na superfície gaussiana é constante, visto que, nesse caso, o campo
deve depender da distância em relação à esfera e, portanto, E pode sair da Integral.
Logo:
No interior da esfera
Para como o campo elétrico varia no interior da esfera, deve-se tomar como superfície Gaussiana
a superfície esférica de raio r no interior da esfera de raio R, como mostra a figura 4. Nesse caso,
4-6
como a carga está uniformemente distribuída pela esfera, a densidade volumétrica de carga, , é a
mesma em todos os pontos da esfera,então pode-se observar que:
onde Vg é o volume da superfície gaussiana escolhida.
Dessa forma:
Os mesmos argumentos dados anteriormente para que o produto escalar E . dA seja E dA e para
que E saia da integral continuam sendo válidos, logo:
Logo:
Portanto, no caso de uma esfera uniformemente carregada:
Campo elétrico no interior e no exterior de uma casca esférica
Para se resolver esse problema, utiliza-se a figura 4 novamente, porém com uma ligeira diferença:
o interior da esfera de raio R é "oco", isto é, tem-se apenas uma casca esférica com carga Q
uniformemente distribuída sobre sua superfície.
No exterior da esfera
Escolhendo a superfície de raio r' como mostrada na figura 4, tem-se, pela lei de Gauss, o mesmo
resultado que foi obtido para o campo no exterior de uma esfera. A carga interna à superfície
gaussiana, qint, é Q nesse caso, como no caso anterior da esfera uniformemente carregada, de
forma que o cálculo para o campo elétrico exterior à da casca esférica se desenvolve da mesma
forma que o cálculo para o campo no exterior à esfera uniformemente carregada, então:
No interior da casca esférica
Escolhendo a superfície gaussiana de raio r, no interior da casca esférica, tem-se:
5-6
Portanto:
Logo:
Portanto, no caso de uma casca esférica uniformemente carregada:
Campo elétrico de um plano infinito
Figura 5: Um exemplo de superfície gaussiana que se deve utilizar para obter o campo de um plano infinito é
como a que está mostrada sobre a placa de baixo do capacitor.
Supõe-se um plano infinito com densidade de carga e se deseja calcular o campo elétrico
produzido por esse plano. Apesar de o problema ser bem diferente do apresentado na figura 5,
visto que, no problema em questão, está-se estudando um plano infinito e não o campo no interior
de um capacitor, é interessante utilizar uma superfície gaussiana de mesma forma que a superfície
retratada na placa de baixo do capacitor da figura 5. Utilizando, portanto, a superfície de um
paralelepípedo cortando o plano infinito como superfície S, tem-se:
Por simetria, o campo elétrico deve apontar para "fora" do plano, isto é, ele aponta na direção
para pontos acima do plano e na direção
para pontos abaixo do plano. Dessa forma, as únicas
superfícies superior e inferior da superfície do paralelepípedo é que serão "furadas" pelo campo
elétrico, por isso:
onde A é a área da superfície superior e inferior da superfície do paralelepípedo. Sabe-se,
também, que : = qint/A, logo : qint = A, portanto:
ou
onde
é um vetor unitário que aponta para fora da superfície do plano.
6-6