Matemática - Conexão Escola

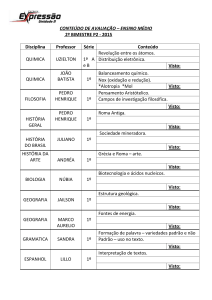
Matemática
Aluno
Caderno de Atividades
Pedagógicas de
Aprendizagem
Autorregulada - 04
7ª Ano | 4° Bimestre
Disciplina
Curso
Bimestre
Ano
Matemática
Ensino Fundamental.
4°
7° ano
Habilidades Associadas
1. Compreender e aplicar o conceito de desigualdade
2. Encontrar soluções particulares de uma inequação do 1º grau.
3. Resolver problemas significativos envolvendo o conceito de desigualdade.
4. Resolver problemas que envolvam o cálculo das médias aritméticas simples e ponderadas
5. Representar dados coletados utilizando gráfico de colunas e de setores.
6. Desenvolver noção intuitiva de probabilidade.
Apresentação
A Secretaria de Estado de Educação elaborou o presente material com o intuito de estimular o
envolvimento do estudante com situações concretas e contextualizadas de pesquisa, aprendizagem
colaborativa e construções coletivas entre os próprios estudantes e respectivos tutores – docentes
preparados para incentivar o desenvolvimento da autonomia do alunado.
A proposta de desenvolver atividades pedagógicas de aprendizagem autorregulada é mais uma
estratégia pedagógica para se contribuir para a formação de cidadãos do século XXI, capazes de explorar
suas competências cognitivas e não cognitivas. Assim, estimula-se a busca do conhecimento de forma
autônoma, por meio dos diversos recursos bibliográficos e tecnológicos, de modo a encontrar soluções
para desafios da contemporaneidade, na vida pessoal e profissional.
Estas atividades pedagógicas autorreguladas propiciam aos alunos o desenvolvimento das
habilidades e competências nucleares previstas no currículo mínimo, por meio de atividades
roteirizadas. Nesse contexto, o tutor será visto enquanto um mediador, um auxiliar. A aprendizagem é
efetivada na medida em que cada aluno autorregula sua aprendizagem.
Destarte, as atividades pedagógicas pautadas no princípio da autorregulação objetivam,
também, equipar os alunos, ajudá-los a desenvolver o seu conjunto de ferramentas mentais, ajudando-o
a tomar consciência dos processos e procedimentos de aprendizagem que ele pode colocar em prática.
Ao desenvolver as suas capacidades de auto-observação e autoanálise, ele passa ater maior
domínio daquilo que faz. Desse modo, partindo do que o aluno já domina, será possível contribuir para
o desenvolvimento de suas potencialidades originais e, assim, dominar plenamente todas as
ferramentas da autorregulação.
Por meio desse processo de aprendizagem pautada no princípio da autorregulação, contribui-se
para o desenvolvimento de habilidades e competências fundamentais para o aprender-a-aprender, o
aprender-a-conhecer, o aprender-a-fazer, o aprender-a-conviver e o aprender-a-ser.
A elaboração destas atividades foi conduzida pela Diretoria de Articulação Curricular, da
Superintendência Pedagógica desta SEEDUC, em conjunto com uma equipe de professores da rede
estadual. Este documento encontra-se disponível em nosso site www.conexaoprofessor.rj.gov.br, a fim
de que os professores de nossa rede também possam utilizá-lo como contribuição e complementação às
suas aulas.
Estamos à disposição através do e-mail [email protected] para quaisquer
esclarecimentos necessários e críticas construtivas que contribuam com a elaboração deste material.
Secretaria de Estado de Educação
2
Caro aluno,
Neste documento você encontrará atividades relacionadas diretamente a algumas
habilidades e competências do 4° Bimestre do Currículo Mínimo. Você encontrará atividades
para serem trabalhadas durante o período de um mês.
A nossa proposta é que você, Aluno, desenvolva estes Planos de Curso na ausência do
Professor da Disciplina por qualquer eventual razão. Estas atividades foram elaboradas a partir
da seleção das habilidades que consideramos essenciais da 7° ano do Ensino Fundamental no
4° Bimestre.
Este documento é composto de um texto base, na qual através de uma leitura
motivadora você seja capaz de compreender as principais ideias relacionadas a estas
habilidades. Leia o texto, e em seguida resolva as Ficha de Atividades. As Fichas de atividades
devem ser aplicadas para cada dia de aula, ou seja, para cada duas horas/aulas. Para encerrar as
atividades referentes a cada bimestre, ao final é sugerido uma pesquisa sobre o assunto.
Para cada Caderno de Atividades, iremos ainda fazer relações diretas com todos os
materiais que estão disponibilizados em nosso site Conexão Professor, fornecendo, desta
forma, diversos materiais de apoio pedagógico para que o Professor aplicador possa repassar
para a sua turma.
Neste Caderno de atividades, vamos estudar um pouco mais sobre o conceito de
inequações e suas aplicações. Na primeira parte abordaremos o estudo de inequações visando
trabalhar com suas propriedades e aplicações em nosso cotidiano. Em seguida, vamos
aprender a ler e interpretar gráficos e tabelas de forma simples e pratica, para que assim que
nosso aluno se depare com gráfico ou tabela ele possa interpretar. Para encerrar a atividade
trabalharemos com a noção de probabilidade de forma simples e de fácil compreensão.
Este documento apresenta 06 (seis) aulas. As aulas são compostas por uma explicação
base, para que você seja capaz de compreender as principais ideias relacionadas às habilidades
e competências principais do bimestre em questão, e atividades respectivas. Leia o texto e, em
seguida, resolva as Atividades propostas. As Atividades são referentes a um tempo de aula. Para
reforçar a aprendizagem, propõe-se, ainda, uma avaliação e uma pesquisa sobre o assunto.
Um abraço e bom trabalho!
Equipe de Elaboração.
3
Sumário
Introdução ............................................................................................
03
Aula 01: Desigualdades .........................................................................
05
Aula 02: Inequação ................................................................................
09
Aula 03: Inequação do 1° grau com uma incógnita ...............................
12
Aula 04: Média aritmética .....................................................................
19
Aula 05: Analise de gráficos e tabelas ...................................................
25
Aula 06: Noção de probabilidade ..........................................................
30
Avaliação ...............................................................................................
34
Pesquisa .................................................................................................
36
Referências: ...........................................................................................
37
4
Aula 1: Desigualdade
Caro aluno, no estudo da matemática trabalhamos com diversos sinais,
provavelmente muitos você já conhece! Alguns deles, são bastante usados no nosso
dia a dia! O sinal de = , por exemplo, significa uma igualdade entre duas quantidades.
É geralmente utilizado na representação de equações.
No entanto, em inúmeros problemas, não precisamos encontrar um único
número como resposta, mas sim um intervalo numérico. Para modelar esses
problemas utilizamos as inequações. Estas são representadas através dos sinais de
(diferente), < (menor que), > (maior que),
(menor ou igual) e
(maior ou igual).
Então, vamos à aula!!
1 – DESIGUALDADE:
Em algumas situações precisamos comparar grandezas que apresentam
diferentes quantidades. Essa comparação pode ser feita através de uma linguagem
matemática, ou seja pode ser expressa por uma desigualdade.
Figura 1
5
Observe que na figura acima podemos fazer as seguintes comparações:
 A altura do ucraniano é diferente da altura do chinês .............................. 2,57 ≠ 2,36
 A altura de Oscar Schmidt é maior que a estatura média do brasileiro ... 2,05 > 1,69
 A altura de Oscar Schimidt é menor que a altura do chinês ..................... 2,05 < 2,36
2 – PROPRIEDADES DAS DESIGUALDADES:
Para que você consiga resolver problemas envolvendo desigualdades se faz
necessário o estudo de algumas propriedades importantes! Leia com atenção as
propriedades a seguir:.
Propriedade 1: ADIÇÃO DE UM MESMO NÚMERO AOS DOIS MEMBROS
Se adicionarmos um número aos dois membros de uma desigualdade
verdadeira, ela permanece verdadeira. Por exemplo, considere a desigualdade abaixo:
7 > 4,
Se adicionarmos 3 aos dois membros, a sentença acima continua verdadeira,
observe:
7+3>4+3
10 > 7.
Propriedade 2: MULTIPLICANDO POR UM NÚMERO POSITIVO NOS DOIS MEMBROS
Consideremos a desigualdade 12 > 5. Vamos multiplicar os dois membros por 2:
12 > 5
12 . 2 > 5 . 2
24 > 10
Observe que a desigualdade continua verdadeira!
Propriedade 3: MULTIPLICAÇÃO POR UM NÚMERO NEGATIVO NOS DOIS MEMBROS
Agora vamos considerar a desigualdade 2 < 20 e vamos multiplicar os dois
membros pelo número ─ 2 aos dois membros:
2 < 20
6
2 . (-2) < 20 . (-2)
─ 4 < ─ 40
Podemos observar que a desigualdade acima é falsa, pois -4 é maior que -20,
assim quando multiplicarmos uma desigualdade por um número negativo devemos
inverter o sinal, ou seja, o sinal < inverte para > e vice-versa. Logo a desigualdade
acima deverá ser:
─ 4 > ─ 40
Agora chegou a hora de testamos o que acabamos de estudar. Então, vamos lá?
Atividade 1
01. Utilize os símbolos de > ou < e complete as lacunas:
a) 7 + 18 ........ 35 – 15
b) 25 ........ 52
c) 13 + 23 ........ (1 + 2)3
d) 3 . 5 ........ 53
e) - 4 . (+2) ........ – 2 . (-4)
02. Observe a figura abaixo e responda:
Qual a expressão algébrica representa a desigualdade que podemos observar nesta
figura?
7
03. Um professor de Matemática solicitou aos seus alunos que escrevessem uma
expressão algébrica para representar esta situação: “A quantidade de pessoas que
realizaram uma prova é representada pela letra x. Se fossem acrescentados 50 pessoas
a esse grupo, o número de pessoas que realizaram a prova ainda será menos que uma
centena.
Como os alunos deveriam representar a desigualdade apresentada na situação
dada pelo professor?
04. Qual o primeiro membro da desigualdade (3 + 5) 2 > 32 + 52 ?
05. Dada a desigualdade –m < 5, pelo princípio multiplicativo, podemos multiplicar os
dois membros por -1. Qual é a nova desigualdade obtida?
8
Aula 2: Inequação
Agora que você já aprendeu o que é uma desigualdade, vamos dar inicio ao
estudo das inequações. Iremos trabalhar este assunto basicamente através de
exemplos para que você possa compreender bem este importante conceito!
Vamos à aula!
1 - DEFINIÇÃO:
Inequação é uma sentença matemática contendo uma ou mais incógnita,
expressa por uma desigualdade. A inequação é muito parecido com a equação, a
diferença é que na equação nós temos uma igualdade representada pelo sinal de =. Na
inequação veremos os sinais de
EXEMPLO 01:
Escreva matematicamente as sentenças abaixo:
a) O dobro de um número é maior que 8;
b) A soma de dois números é menor que 50.
Resolução:
a) Neste caso, temos uma inequação com uma única incógnita. Sabemos que o dobro
de um número x é 2x. Logo, escrevendo matematicamente a sentença teremos: 2x > 8.
b) Neste caso, temos uma inequação com duas incógnitas, x e y. Escrevendo
matematicamente a sentença teremos: x + y < 50.
9
EXEMPLO 02:
Um retângulo tem “a” metros de comprimento e “b” metros de largura, e um triângulo
equilátero tem 3 metros de lado. Que sentença matemática pode expressar o fato de o
perímetro do retângulo ser maior que o perímetro do triângulo equilátero?
Resolução:
Sendo P1 o perímetro do retângulo e P2 o perímetro do triângulo equilátero,
temos:
P1 = 2a + 2b
e
P2 = 3 + 3 + 3 = 9
Como a situação diz que P1 > P2 , então, 2a + 2b > 9
A partir do século XVII, as sentenças matemáticas passaram a ser
escritas com letras que representam números desconhecidos.
As sentenças matemáticas representadas por igualdades em que
um ou mais elementos são desconhecidos são chamadas de equações.
Da mesma forma, as sentenças matemáticas representadas por
desigualdades em que um ou mais elementos são desconhecidos são
chamadas de inequações.
10
Assim como nas equações, nas inequações também temos dois membros:
5y + 7
1º membro
<
17
2º membro
56
<
k-z
1º membro 2º membro
Chegou a hora de ver se você entendeu direitinho tudo que acabamos de ver
na aula 2. Vamos realizar nossas atividades?
Atividade 2
01. A sentença matemática 4y – 5 > 3 é uma inequação? Justifique a sua resposta.
02. Para cada item abaixo, escreva a inequação correspondente:
a) O triplo de um número y diminuído de 10 é menor que 18.
b) Três quartos de k é maior que o triplo de x.
c) A diferença entre o dobro de y e 7 é menor que 10.
d) A soma de um número k com sua metade é menor que 2.
e) A diferença entre o quíntuplo de um número x e o triplo desse próprio número é
maior que a terça parte desse número mais um.
11
03. Escreva a inequação que representa o perímetro das figuras abaixo, sabendo-se que
o perímetro do quadrado é menor que o perímetro do retângulo.
04. Uma motocicleta custa x reais e um automóvel custa y reais. Escreva a inequação que
corresponde a condição: “duas motocicletas e um automóvel custam juntos mais de 50
mil reais”.
05. Escreva a inequação que representa a área da figura abaixo, sabendo que essa área é
menor que 50m2.
06. Em um vagão de trem cabem x toneladas de carvão. Se 3 toneladas caírem durante o
transporte, sobrará menos que a metade da capacidade do vagão. Escreva a inequação
que representa esse fato.
12
Aula 3: Inequação do 1º Grau com uma Incógnita
Agora que já vimos o que é uma inequação, que tal aprendermos a calcular a
raiz de uma inequação do primeiro grau? Veja como é simples! Acompanhe os
exemplos que iremos apresentar com bastante atenção!
1 ─ INEQUAÇÃO DO 1° GRAU
Inequação do 1º grau com uma incógnita é toda inequação que, sofrendo
transformações oportunas, assume umas das formas abaixo:

ax>b

ax<b

ax≥b

ax≤b
com a ≠ 0
Achou complicado entender essa explicação apenas com símbolos? Apenas
queremos que você aprenda a reconhecer uma inequação do 1° grau. Veja alguns
exemplos numéricos:

5x > 20  incógnita x

3k < 15  incógnita k

8y ≥ 10  incógnita y

-2z ≤ -6  incógnita z
2 ─ SOLUÇÃO DE UMA INEQUAÇÃO:
Resolver uma inequação do 1º grau com uma incógnita significa determinar os
valores do conjunto universo que tornam verdadeira a desigualdade que representa
13
essa inequação. Logo, a solução de uma inequação raramente será dada por um único
valor.
Vamos resolver as desigualdades apresentadas nos exemplos a seguir isolando
a incógnita, de preferência no 1° membro. Observe:
EXEMPLO 01:
Vamos resolver a inequação 5x + 4
>
2x + 7, sendo U = Q
2° membro
1° membro
Resolução:
5x + 4 > 2x + 7
5x – 2x > 7 – 4
3x > 3
x>
x>1
No exemplo acima vimos que todas as vezes que trocamos de membros
trocamos o sinal da desigualdade. Lembra da propriedade 3 ?
Da inequação x > 1, podemos dizer que todos os números racionais maiores que
1 formam o conjunto solução da inequação dada que representamos por:
S = { x  Q / x > 1}
EXEMPLO 02:
Agora vamos achar o conjunto solução (S) da inequação 3 . (y – 1) – 3 (2y + 3) < 6,
sendo U = Q.
Resolução:
3 . (y – 1) – 3 (2y + 3) < 6
3y – 3 – 6y – 9 < 6
14
3y – 6y < 6 + 3 + 9
– 3y > 18  multiplicamos por (-1) inverte-se o sinal da desigualdade
3y < – 18
y<–
y<-6
S = { x  Q / y < ─ 6}
Observe que este conjunto solução significa que qualquer valor maior que ─6,
satisfaz a inequação, por exemplo: ─ 5, ─ 4, ─ 3, ─2, ...
ATENÇÃO!!!
Toda vez que ocorrer a multiplicação por -1,
o símbolo da desigualdade deverá ser
substituído pelo seu inverso.
EXEMPLO 03:
Verifique se os números racionais − 9 e +6 fazem parte do conjunto solução da
inequação 5x – 3 . (x + 6) > x – 14.
Resolução:
Primeiramente vamos resolver a inequação.
5x – 3 . (x + 6) > x – 14
5x – 3x + 18 > x – 14
5x – 3x – x > – 14 + 18
5x – 4x > 4
x>4
15
Agora vamos fazer a verificação:
 Para − 9, temos: ─ 9 > 4 (sentença falsa, pois -9 é menor que 4)
 Para 6, temos: 6 > 4 (sentença verdadeira)
Então, podemos concluir que o número 6 faz parte do conjunto solução (S) da
inequação dada. Já o número -9 não faz parte desse conjunto.
EXEMPLO 04:
Verifique para quais os valores podemos assumir que o perímetro do retângulo seja
maior que o perímetro do quadrado:
Resolução:
Primeiramente vamos achar a inequação que representa a situação
apresentada:
2 . x + 2 . 5 > 4 . 11
Agora, vamos resolver a inequação:
2x + 10 > 44
2x > 44 – 10
2x > 34
x>
x > 17
S = { x  Q / x > 17}
Desse modo concluímos que para qualquer valor maior que 17 satisfaz a
condição proposta no problema.
16
Que tal treinar o que acabamos de aprender e começar a resolver algumas
inequações? Então vamos lá!
Atividade 3
01. Quais os números racionais representam a solução de cada uma das inequações
abaixo:
a) x + 15 > 21
b) x – 18 < 23
c) 11 – 9x ≥ 2x
d) 8x + 19 ≤ 10x + 11
e) 3 . (x – 1) – 2x ≥ 13
f) 9 . (x – 2) – 5 . (x – 3) ≤ 1
02. Verifique se o número 3 pertence ao conjunto solução da inequação
2 . (x – 2) < 3x – 6.
03. Dados os números abaixo. Assinale quais deles pertencem ao conjunto solução da
inequação 3 . (2x – 1) < 5x – 1 ?
(A) – 6
(B) – 3
(C) 2
(D) 0
(E) 3
(F) 6
17
04. Observe a figura abaixo e calcule os valores, que o lado do triângulo equilátero
pode assumir para que o perímetro desse triângulo seja maior que o perímetro do
retângulo dado.
18
Aula 4: Média Aritmética
A média aritmética simples também é conhecida apenas por média. É a medida
de tendência central mais utilizada no nosso cotidiano e é também, entre as medidas
de posição, a mais intuitiva de todas. Ela está tão presente em nosso dia-a-dia que
qualquer pessoa entende seu significado e a utiliza com frequência.
Vamos à aula!
1 ─ MÉDIA ARITMÉTICA:
A média aritmética de um conjunto de valores numéricos é calculada somandose todos estes valores e dividindo-se o resultado pelo número de elementos
somados. Observe como é simples! Vamos calcular a média entre 5, 10 e 6:
M
=
=
=7
Esse tipo de cálculo é muito utilizado em campeonatos de futebol, por exemplo,
no intuito de determinar a média de pontos que um time precisa para ser campeão.
Observe a reportagem publicada em 22 de outubro de 2013, conforme texto
abaixo:
“Cruzeiro faz contas e busca vitórias em casa para alcançar média de campeões”
Os últimos quatro jogos não assustam o Cruzeiro. Três derrotas (São Paulo,
Atlético-MG e Coritiba) e uma vitória magra (Fluminense) não tiveram força suficiente para
tirar a diferença que o clube celeste tem para o vice-líder do Campeonato Brasileiro, o
Grêmio – hoje, de nove pontos (62 a 53).
Os mineiros já começam a fazer as contas pelo título. Com média de 72,2 pontos
para o campeão nos últimos cinco anos, o clube precisa de todas as vitórias dentro de
casa para atingir e ultrapassar a marca e conquistar a sonhada taça.
19
Para entendermos os cálculos realizados na reportagem, devemos relembrar a
pontuação dos times campeões nos últimos 5 anos. Para isso observe a tabela a seguir:
Ano do Campeonato
Campeão
Pontuação
2008
São Paulo
75
2009
Flamengo
67
2010
Fluminense
71
2011
Corinthians
71
2012
Fluminense
77
Observe como a conta é simples!
Para chegar ao resultado apresentado na reportagem, 72,2, basta somar todos os
pontos dos cinco times e dividir pelo número de times. Ou seja:
M=
=
= 72,2
Perceba ainda que o Cruzeiro tem 62 pontos e 12 pontos para disputar em casa.
Se conseguir todas as vitórias a equipe chega aos 74 pontos e ultrapassa a média dos
últimos vencedores.
Viu como entender sobre média ajuda a compreender um pouco de futebol?
A média aritmética também é utilizada nas escolas para calcular a média final dos
alunos e nas pesquisas estatísticas, pois os resultados determinam o direcionamento das
ideias expressas pelas pessoas pesquisadas.
EXEMPLO 01:
Vamos observar as notas bimestrais de um aluno e calcular a sua média anual:
20
Bimestre
Nota
1º
6,0
2º
4,5
3º
8,0
4º
7,5
Resolução:
Como já foi dito anteriormente, para calcular a média anual, devemos somar os
valores de todas as notas. Como temos quatro notas, devemos dividir o resultado por 4.
Observe:
M=
=
= 6,5
Logo, podemos concluir que a média anual do aluno foi 6,5.
EXEMPLO 02:
Durante uma semana, o valor diário do dólar foi observada e anotada na tabela abaixo :
Dia da Semana
Dólar
Segunda
R$ 2,80
Terça
R$ 2,70
Quarta
R$ 2,50
Quinta
R$ 2,60
Sexta
R$ 2,70
Determine o valor médio do preço do dólar nesta semana:
Resolução:
Como temos 5 valores, um para cada dia da semana. Para encontrar a média
basta calcular a soma e dividir por 5, conforme calculo abaixo:
21
M=
=
= 2,66
O valor médio do dólar na semana apresentada foi de R$ 2,66.
EXEMPLO 03:
Uma pesquisa realizada num grupo de 12 alunos, com o objetivo de obter a
idade média dos alunos desse grupo, obteve os resultados tabulados na tabela abaixo:
Idade
Número de Alunos
12 Anos
2
13 Anos
4
14 Anos
3
15 Anos
2
16 Anos
2
Calcule a idade média dos alunos desse grupo:
Resolução:
Para calcularmos a idade média dos alunos desse grupo, precisaremos
multiplicar o número de alunos pela idade correspondente a esse número, somarmos
os resultados obtidos e dividirmos essa soma pelo número total de alunos.
Observe:
M=
=
M=
M=
= 15
A média de idade dos alunos desse grupo é 15 anos.
22
Vamos exercitar um pouco sobre o que você acabou de aprender? Resolva as
atividades a seguir e qualquer dúvida retome os exemplos acima!
Atividade 4
01. Calcule a média aritmética em cada um dos seguintes casos:
a) 15 ; 48 ; 36
b) 80 ; 71 ; 95 ; 100
c) 59 ; 84 ; 37 ; 62 ; 10
d) 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9
e) 18 ; 25 ; 32
f) 91 ; 37 ; 84 ; 62 ; 50
02. Um grupo de alunos apresenta as idades de 10, 12, 15 e 17 anos. Se um aluno de
11 anos se juntar ao grupo, qual será a média de idade dos alunos desse grupo ?
03. No dia da realização do SAERJ, uma escola fez o levantamento do número de
alunos presentes em cada turma e os resultados foram tabulados e apresentados na
tabela abaixo:
Turma
1001
1002
1003
2001
2002
2003
3001
3002
3003
Quantidade
de alunos
32
31
29
30
33
28
27
29
31
A média de alunos por turma foi de:
23
04. João deseja calcular a média das notas que tirou em cada uma das quatro matérias
a seguir. Ajude João a calcular essas médias:
Inglês
1ª prova
6,5
2ª prova
7,8
3ª prova
8,0
4ª prova
7,1
Português
1ª prova
7,5
2ª prova
6,9
3ª prova
7,0
4ª prova
8,2
História
1ª prova
5,4
2ª prova
8,3
3ª prova
7,9
4ª prova
7,0
Matemática
1ª prova
8,5
2ª prova
9,2
3ª prova
9,6
4ª prova
10,0
05. Uma criança comprou 5 doces a R$ 1,80 cada um, 3 doces a R$ 1,50 e 2 doces a
R$ 2,00 cada. Qual o preço médio pago por cada doce?
24
Aula 5: Análise de gráficos e tabelas.
Caro aluno, nesta aula nós iremos analisar alguns gráficos e tabelas. Você vai
perceber que estudar esse assunto será muito importante para que você consiga
compreender o que passa em nosso dia a dia. Além disso, este estudo lhe ajudará a
entender, como organizar as informações que queremos passar de forma resumida.
Leia com atenção e boa aula.
1 ─ TABELAS:
Certamente, você sabe o que é uma tabela! E já deve ter visto várias no nosso
dia a dia. Uma tabela nos ajuda a organizar dados recolhidos, podendo assim escrever
essas informações de forma reduzida e de fácil compreensão, veja a situação problema
abaixo.
Na tabela abaixo vamos ver a classificação do campeonato Brasileiro 2013 na
13° rodada.
Figura 2
25
A tabela acima apresenta algumas informações sobre os times que disputam a
série A do campeonato. Ela está apresentando em uma tabela com informações
coletadas até a rodada citada acima.
2 ─ GRÁFICOS:
Os gráficos representam outra forma de apresentar os resultados obtidos de uma
amostra. Os gráficos podem ser representados de diversas maneiras.
Alguns
elementos dos gráficos nos ajudam a compreender melhor as
informações, o que nós temos que levar em consideração.
 Título: É o nome que se dá à pesquisa, ou à pergunta que foi feita.
 Legenda: Discrimina os itens do gráfico.
 Eixos: No eixo horizontal, temos os elementos do gráfico e no vertical,
temos os números referentes a quantidade.
Agora vamos estudar alguns tipos de gráficos!
2.1 – GRÁFICOS DE COLUNAS:
O gráfico é representado por colunas de bases iguais que ficam apoiadas no eixo
horizontal, nesses gráficos não importa a largura da coluna, pois só o que vamos
considerar é a altura. Ela nos dará a informação que queremos retirar do gráfico.
Figura 3
26
2.2 – GRÁFICOS DE BARRAS:
O gráfico de barras é parecido com o de colunas. Nele temos dois eixos,
título e legenda. A única diferença é que os retângulos estão apoiados no eixo vertical.
Figura 4
No gráfico acima podemos ver uma pesquisa feita medindo o desempenho dos
alunos em matemática.
2.3 – GRÁFICOS DE SETORES:
O gráfico nos faz lembrar uma pizza, pois seu formato circular e suas divisões são
semelhantes. Veja como são passadas as informações.
Figura 5
27
Observe no exemplo que o gráfico foi dividido em setores (fatia), que são
determinados pelo ângulo central do circulo. Para encontrar o ângulo do setor basta
multiplicar a taxa percentual por 360°.
Atividade 5
01. O gráfico abaixo mostra uma pesquisa feita com crianças de uma cidade no interior
do Rio de Janeiro, analise os gráficos e responda.
a) Que porcentagem de crianças tem os olhos negros?
b) Qual a diferença entre as crianças de olhos azuis e as de olhos verdes?
02. No gráfico abaixo, veremos uma pesquisa de opinião onde as pessoas avaliaram o
que cada um acha do time de futebol que torce:
28
a) Quantas pessoas avaliaram como ótimo o time que torce?
b) Quantas pessoas acham o próprio time regular?
03. Analise o gráfico abaixo e responda.
a) Qual foi o ano que a empresa faturou 5 000 000?
b) Quanto ela faturou no ano de 2012?
04. No gráfico abaixo, vemos alguns dados sobre o Maracanã, com base nesse gráfico
responda.
a) Qual time teve melhor média de público?
b) Quais times tiveram público médio inferior a 50 000?
29
Aula 6: Noção de probabilidade.
Na aula de hoje, nós iremos desenvolver a noção de probabilidade, que é um
tipo especial de razão. Esse conteúdo desenvolve nosso raciocínio lógico, nos dando
uma ideia numérica das chances do acontecimento de um evento. Leia com atenção e
boa aula!
Para iniciar a aula, imagine que seu professor de matemática, para ensinar
probabilidade para a sua turma, colocou 8 bolas dentro de um saco, sendo 3 amarelas
e 5 vermelhas, em seguida perguntou: ─ Qual é a chance de se retirar ao acaso uma
bola, e sair uma bola de cor vermelha?
Figura 6
Certamente você ficou curioso com a resposta, não é mesmo? Esse é um
exemplo que podemos usar para que os você compreenda melhor este assunto.
Vamos a aula!
1. EVENTOS POSSÍVEIS:
Chamamos de EVENTOS POSSÍVEIS os resultados possíveis de ocorrer, ou seja,
todos os eventos que podem acontecer!
Entendeu? É simples, observe a situação a seguir!
EXEMPLO 1:
No lançamento de um dado, por exemplo, quando lançamos um dado não
viciado, os números de 1 a 6 tem a mesma chance de sair. Ao lançar um dado, podemos
30
ter 6 diferentes resultados. Então, dizemos que: U = {1,2,3,4,5,6},
Figura 7
2. EVENTO FAVORÁVEL:
É o número de chances favoráveis, o que é convenente.
EXEMPLO 02:
Se no lançamento me for conveniente que caia um número par, ou seja, os
números 2, 4 ou 6. Eu tenho 3 eventos favoráveis.
3. CONCEITO DA PROBABILIDADE:
Como foi dito acima a probabilidade é uma razão especial. Para encontrá-la
basta encontrar a razão entre os eventos favoráveis sobre os possíveis.
EXEMPLO 03:
Em um lançando de um dado não viciado para o alto, qual a probabilidade de:
a) Cair com o número 3 voltado para cima?
b) Qual é a chance de cair um número ímpar?
Resolução:
a) Nesse exemplo podemos perceber que os eventos possíveis serão o número de faces
do dado, então os eventos possíveis {1,2,3,4,5,6} e número total de eventos é 6.
31
Em seguida veremos que o evento favorável é o 3 e o número de eventos é igual
a 1, pois há um só elemento que satisfaz a condição desejada. Então, calculando temos:
Esta probabilidade significa que temos uma chance em seis possibilidades.
b) Vimos acima que possíveis valores para o dado são = {1,2,3,4,5,6} ,logo o número de
eventos possíveis = 6.
Para encontrar os favoráveis, temos que olhar acima e ver quais são os ímpares
e teremos favoráveis = {2,4,6}, aplicando a fórmula teremos.
Então temos uma chance em duas.
Agora vamos verificar se você aprendeu. Resolva os exercícios abaixo e em caso
de dúvidas retorne aos exemplos.
32
Atividade 6
01. Um dado não viciado é lançado para o alto, qual é a probabilidade de:
a) Cair o número 5 voltado para cima?
________________________________________________________________________
________________________________________________________________________
b) Qual a probabilidade de sair um número impar?
________________________________________________________________________
________________________________________________________________________
02. Se jogarmos uma moeda para o alto, qual é a probabilidade de sair cara?
________________________________________________________________________
________________________________________________________________________
03. Em uma caixa há 6 bolas, 2 verdes e 4 pretas. Responda:
a) se retirarmos uma bola ao acaso, qual a probabilidade de sair verde?
________________________________________________________________________
________________________________________________________________________
b) se retirarmos uma bola ao acaso, qual a probabilidade de sair preta?
________________________________________________________________________
________________________________________________________________________
04. Em um baralho há 52 cartas, qual a probabilidade de retirarmos uma carta de paus?
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
________________________________________________________________________
33
Avaliação
Nesta aula você encontrará algumas atividades para relembrar e aplicar o que
estudou até aqui. São atividades simples e com certeza você consegue realizar!
01. Qual é a solução da inequação 3a – 4 < 8:
(A) a < 2
(B) a < 3
(C) a < 4
(D) a < 5
02. O triplo de um número mais dez é menor que vinte. Qual das inequações abaixo
representa o enunciado?
(A) 2x – 9 > 10
(B) 2x – 10 < 20(C) 3x + 10 > 20
(D) 3x + 10 < 20
03. Qual dos números abaixo está no conjunto solução da inequação 2(x + 1)
x + 5:
(A) 0
(B) 1
(C) 2
(D) 3
34
04. O dobro de um número somado a 6 é maior que seu quádruplo diminuído 6. Esse
número é necessariamente:
(A) positivo.
(B) negativo.
(C) maior que 6.
(D) menor que 6.
05. Analisando o gráfico abaixo, responda:
De acordo com o gráfico, em quais meses do ano não chove?
(A) MAR e ABR
(B) JUL e AGO
(C) MAI e DEZ
(D) SET e OUT
06. Se lançarmos um dado perfeito para o alto, qual a probabilidade de sair um
número maior que 3.
(A) ½
(B) ¼
(C) 1/3
(D) 2/6
35
Pesquisa
Caro aluno, agora que já estudamos todos os principais assuntos relativos ao 2°
bimestre, é hora de discutir um pouco sobre a importância deles na nossa vida. Então,
vamos lá?
Leia atentamente as questões a seguir e através de uma pesquisa responda
cada uma delas de forma clara e objetiva.
ATENÇÃO: Não se esqueça de identificar as Fontes de Pesquisa, ou seja, o nome dos
livros e sites os quais foram utilizados.
I – Apresente alguns exemplos de situações reais nas quais podemos encontrar
gráficos e tabelas.
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
II – Apresente alguns exemplos reais, em que a inequação vai nos ajudar a encontrar a
solução de um problema.
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
III – Agora pesquise em jornais e revistas alguns exemplos de gráficos. Recorte e
destaque o Título, e diga qual o tipo do gráfico que você escolheu:
(ATENÇÃO: Fazer esta parte da atividade na parte folha separada! )
36
Referências
[1] Bianchini, Edwaldo. Matemática. 6 ed. São Paulo: Moderna, 2006.
[2] Bosquilha, Alessandra. Mini-manual compacto de matemática: teoria e Prática. 2
ed. São Paulo: Rideel, 2003.
[3] Dante, Luiz Roberto. Tudo é Matemática. Volume 1, 3ed. São Paulo: Ática, 2003.
[4] Ferreira, Marcus Vinicius Reis. Geometria Analítica e Espacial. 1 ed. Rio de Janeiro,
2004.
[5] Giovanni, José Ruy, 1937 – A conquista da matemática. Volume 1, Edição renovada.
São Paulo: FTD, 2007.
Fonte das Imagens
[1] Figura 1 : Fonte: http://g1.globo.com/Noticias/Mundo/0,,MUL84760-5602,00UCRANIANO+E+O+NOVO+HOMEM+MAIS+ALTO+DO+MUNDO.html
[2] Figura 2: Fonte:http://www.youtube.com/watch?v=kVxgmXsXmFE&hd=1
[3] Figura 3: Fonte:http://revistaescola.abril.com.br/fundamental-1/leitura-graficosanimais-zoologico-643178.shtml
[4] Figura 4 Fonte:http://www.brasilescola.com/matematica/graficos.htm
[5] Figura 5 Fonte: http://www.mundoeducacao.com/matematica/graficos-setores.htm
[6] Figura 6: Fonte: http://www.educ.fc.ul.pt/icm/icm98/icm25/pag4.htm
[7] Figura 7: fonte: http://galeria.colorir.com/jogos/dado-pintado-por-juh-dado121001.html
37
Equipe de Elaboração
COORDENADORES DO PROJETO
Diretoria de Articulação Curricular
Adriana Tavares Mauricio Lessa
Coordenação de Áreas do Conhecimento
Bianca Neuberger Leda
Raquel Costa da Silva Nascimento
Fabiano Farias de Souza
Peterson Soares da Silva
Marília Silva
COORDENADORA DA EQUIPE
Raquel Costa da Silva Nascimento
Assistente Técnico de Matemática
PROFESSORES ELABORADORES
Ângelo Veiga Torres
Daniel Portinha Alves
Fabiana Marques Muniz
Herivelto Nunes Paiva
Izabela de Fátima Bellini Neves
Jayme Barbosa Ribeiro
Jonas da Conceição Ricardo
Reginaldo Vandré Menezes da Mota
Tarliz Liao
Vinícius do Nascimento Silva Mano
Weverton Magno Ferreira de Castro
REVISÃO DE TEXTO
Isabela Soares Pereira
38