Diagrama Tensão (s) x Deformação (e)

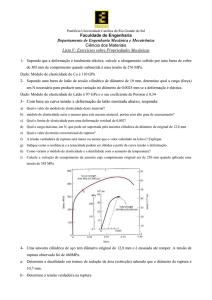
Diagrama Tensão (s) x Deformação (e)
O diagrama s x e mostra uma relação entre estas duas grandezas através de uma
linha definida em um gráfico x/y onde o eixo x representa as deformações e o eixo y
representa as tensões.
A obtenção do diagrama tensão x deformação deve ser realizada para os diferentes
tipos de material podendo ser feita através de um ensaio de tração.
Realização do ensaio de tração:
1. Toma-se uma barra circular de material homogêneo, com uma determinada seção
transversal A0. Sobre esta barra, marca-se dois pontos distantes L0 um do outro.
Ensaio de Tração antes da Aplicação da Carga
2.Submete-se esta barra a uma força normal N que aumenta gradativamente.
3. Para cada valor de N, calcula-se um dLP = L - L0
4. Para cada valor de N, mede-se as modificações no diâmetro.
Ensaio de Tração após da Aplicação da Carga
5. Para cada valor de N, calcula-se a tensão s = N / A0, ou seja, a medida que altera-se o
valor da carga aplicada, altera-se o valor da tensão.
6. Para cada valor de N, calcula-se a deformação específica e = dLP/L0
7. Marca-se em gráfico os valores de s x e obtendo-se então o diagrama tensão x
deformação.
A partir da relação entre tensão e deformação obtida com o ensaio anterior, pode-se
definir dois tipos de materiais:
Materiais dúteis
Materiais frágeis

Materiais dúteis (aço estrutural e outros metais)
Diagrama tensão x deformação
su: tensão última (máxima tensão que se
atinge)
sR: tensão de ruptura (tensão que, se atingida,
provoca a ruptura do material)
se: tensão de escoamento
eR: deformação de ruptura (deformação que,
se atingida, provoca a ruptura do material)
Fases de evolução do diagrama
1. Aumento lento do comprimento (pequena deformação), diretamente proporcional a uma
grande carga aplicada (trecho reto da origem até a tensão de escoamento - se), com grande
coeficiente angular (reta "quase" na vertical).
2. Longa deformação com pouco aumento da carga aplicada, ou seja, pequena variação da
tensão (escoamento).
3. Aumento da deformação proporcional ao aumento da carga aplicada, ou seja, da tensão.
Este aumento ocorre até que a carga aplicada atinja um valor máximo, ou, uma tensão
última - su (recuperação).
4. Diminuição do diâmetro do corpo (estricção). Uma diminuição da carga aplicada é
suficiente para manter a deformação até a ruptura. (sR: tensão de ruptura; eR: deformação de
ruptura).

Materiais frágeis (ferro fundido, vidro, pedra...)
Diagrama tensão x deformação
su: tensão última (máxima tensão que se
atinge)
sR: tensão de ruptura (tensão que, se
atingida, provoca a ruptura do material)
eR: deformação de ruptura (deformação
que, se atingida, provoca a ruptura do
material)
Fases da evolução do diagrama
Aumento da deformação proporcional ao aumento da carga aplicada até que se atinja a
deformação de ruptura (eR) que corresponde à tensão de ruptura (sR) que é igual à tensão
última (su).
σ
σ
d
σ
d
d
U
Y
B
Y
P
O
?
Є
Figura 1.a
O
O
?1
Figura 1.b
?
?
Є
Є
Figura 1.c
PROPRIEDADES MECÂNICAS
O diagrama tensão deformação permite caracterizar diversas propriedades do material, que
se defini a seguir.
LIMITE DE PROPORCIONALIDADE
Muito próximo a P, existe um ponto na curva tensão-deformação, ao qual
corresponde o limite de elasticidade; ele representa a tensão máxima que pode ser aplicada
à barra sem que apareçam deformações residuais, ou permanentes, após a retirada integral
da carga externa. Para muitos materiais os valores dos limites de elasticidade e
proporcionalidade são praticamente iguais e esses termos são, então empregados como
sinônimos. Nos casos em que eles são diferentes, em geral o limite de elasticidade é maior
do que o de proporcionalidade.
REGIÃO ELÁSTICA
O trecho da curva tensão-deformação, compreendido entre a origem e o limite de
proporcionalidade.
REGIÃO PLÁSTICA
Chama-se região plástica o trecho do diagrama compreendido entre o limite de
proporcionalidade e o ponto correspondente à ruptura do material.
LIMITE DE ESCOAMENTO
A tensão corresponde ao ponto Y tem o nome de limite de escoamento. A partir
deste ponto aumentam as deformações sem que se altere, praticamente, o valor da tensão.
Quando se atinge o limite de escoamento, diz-se que o material passa a escoar-se. Alguns
materiais apresentam dois pontos para os quais aumentam as deformações sob tensão
constante. Esses pontos, em geral muito próximos um do outro, recebem os nomes de
limites de escoamento superior e inferior.
LIMITE DE RESISTÊNCIA OU RESISTECIA A TRAÇÃO
A tensão correspondente ao ponto B recebe o nome de limite de ruptura; é a que
corresponde a ruptura do corpo de prova.
MÓDULO DE RESILIÊNCIA
É a energia que o corpo armazena, por unidade de volume, quando a partir de zero,
se eleva o valor da tensão até o limite de proporcionalidade. Seu valor pode ser obtido
calculando-se a área hachurada na fig.1.a, é evidente que a dimensão do módulo de
resiliência é a de um trabalho. Assim, a resiliência de um material e a capacidade de
absorver energia na região elástica.
MÓDULO DE TENACIADADE
É energia que o corpo armazena, por unidade de volume, quando, a partir de zero, se
eleva o valor da tensão até o limite de ruptura. Seu valor pode ser obtido, no diagrama
tensão-deformação, com cálculo da área limitada pela curva, os eixos coordenados e a
ordenada correspondente ao ponto de ruptura. A tenacidade de um material é a capacidade
de absorver energia na região plástica.
REDUÇÃO PERCENTUAL DE ÁREA
A relação, em percentagem, entre a diminuição da área da secção transversal (
relativamente a área inicial), por ocasião da ruptura, e a área inicial, recebe o nome de
redução percentual da área da secção transversal. Observa-se que a tração axial, ou tração
simples, a área da secção transversal diminui, mas nos cálculos de δ introduz-se, sempre, a
área original. Por esse motivo é que a curva tensão-deformação tem o aspecto indicado na
fig.1.a. Quanto mais crescem as deformações, mais importante é considerar os valores
correspondentes da área da seção transversal (que diminui) e, se levar isso em conta,
obtém-se um diagrama real, em lugar do convencional. Esse diagrama tem o aspecto da
curva que se representa, em verde, na fig.1.a.
ALONGAMENTO PERCENTUAL
Exprimi-se, em porcentagem, o acréscimo de comprimento (de referência), depois
da ruptura, em relação ao comprimento inicial, tem-se o alongamento percentual. Quer a
redução percentual da área, quer o alongamento percentual, servem para caracterizar,
também, a ductibilidade do material.
TENSÃO ADMISSÍVEL
As propriedades mecânicas, relativa a resistência, permite que se fixe a tensão admissível
do material. Todas as tensões admissíveis estão na região elástica. Obtém-se essa tensão
dividindo-se ou o limite de escoamento ou o limite de resistência por um número, maior
que a unidade, denominado coeficiente de segurança. A fixação do coeficiente de segurança
é feita nas normas de cálculo e, algumas vezes, pelo próprio calculista, baseado em
experiências e de acordo com o seu critério.
ENDURECIMENTO DE DEFORMAÇÃO
Se um material dúctil pode ser tensionado consideravelmente além do limite de
escoamento, sem ruptura, dizemos que endurece sob deformação. Isto se verifica para
metais estruturais.
A curva tensão-deformação de um material frágil, isto é, não linear, como se indica
na fig1.b, caracteriza diversas outras propriedades, que se distinguem daquelas que
correspondem ao diagrama linear e que a seguir se define.
LIMITE D ESCOAMENTO
Denomina-se, agora, limite de escoamento a tensão que corresponde a uma
deformação permanente, pré-fixada, depois do descarregamento do corpo de prova. Essa
deformação permanente é, às vezes, em 0,0035cm/cm. Esses valores são arbitrários mas,
em geral, fixados nas especificações. Na fig.1.b fixou-se a deformação permanente ε1; para
determinar o limite de escoamento, traça-se a reta O’Y paralela á tangente à curva que passa
pela origem. Sua intersecção, com a curva, determina o ponto Y que corresponde ao limite
de escoamento procurado.
MÓDULO TANGENTE
A tangente trigonométrica, do ângulo de a tangente a curva tensãodeformação, na origem, forma com o eixo dos ε,recebe o nome de módulo tangente.
Existem outras característica do material, que são utilizadas no calculo e no
dimensionamento das peças.
Aplicação:
1) Uma barra de 3m de comprimento tem secção transversal retangular de 3cm por
1cm. Determinar o alongamento produzido pela força axial de 6Kg, sabendo que E = 2000t
/ cm2.
2) A barra de aço da figura abaixo tem secção transversal de área S = 10cm 2 e está
solicitada pelas forças axiais que aí se indicam. Determinar o alongamento da barra,
sabendo que E = 2100t / cm2.
10000Kg
10000Kg
A
C
B
2000Kg
3000Kg
D
9000Kg
3) A treliça Howe é parte integrante de um dos blocos do Navio Rainha Ipojuca e
suporta a força de 54t. Determinar as áreas da secção transversal das barras DE e AC,
sabendo que a tensão admissível do material, sob tração, é de 1400 kg/cm 2. sendo de 2m o
comprimento da barra DE, pergunta-se qual seu alongamento admitido, para módulo de
elasticidade do material, o valor E = 2,1x106.
ED
AB
B
4
5
D
F
2m
A
3
A
1,5 m
1,5 m
E 1,5 m
C
1,5 m
AC
D
EG
EC
H
G
27 t
54 t
54 t
4) O Navio Ifpe possui um suporte de molinete em forma de duas barras
prismáticas, rigidamente ligadas entre si, suportando a carga axial de 4500kg, como
indicada na figura. A barra superior é de aço, tem 10m de comprimento e seção transversal
de 65m2 de área. A barra inferior é de latão, tem 6m de comprimento e seção transversal de
52cm2 de área. Tendo-se, para o aço, γ = 7800kg/m3 e E = 2,1x106kg/cm2 e, para o latão,
γ = 8300kg/m3 e E = 0,9x106kg/cm2, pedem-se as tensões normais máximas, em cada
material.
A
A
10 m
B
B
6m
C
C
4500 kg
.σ =P/S