Impulso - Lógico Cursos Aliados

1. Um objeto de massa m escorrega com velocidade V sobre uma superfície horizontal sem
atrito e colide com um objeto de massa M que estava em repouso. Após a colisão, os dois
objetos saem grudados com uma velocidade horizontal igual a V 4. Calcule a razão M m.
a) 1 3
b) 1 2
c) 1
d) 2
e) 3
2. Um jogador de tênis, durante o saque, lança a bola verticalmente para cima. Ao atingir sua
altura máxima, a bola é golpeada pela raquete de tênis, e sai com velocidade de 108 km h na
direção horizontal. Calcule, em kg m s, o módulo da variação de momento linear da bola entre
os instantes logo após e logo antes de ser golpeada pela raquete.
Dado: Considere a massa da bola de tênis igual a 50 g.
a) 1,5
b) 5,4
c) 54
d) 1.500
e) 5.400
3. Na olimpíada, o remador Isaquias Queiroz, ao se aproximar da linha de chegada com o seu
barco, lançou seu corpo para trás. Os analistas do esporte a remo disseram que esse ato é
comum nessas competições, ao se cruzar a linha de chegada.
Em física, o tema que explica a ação do remador é:
a) o lançamento oblíquo na superfície terrestre.
b) a conservação da quantidade de movimento.
c) o processo de colisão elástica unidimensional.
d) o princípio fundamental da dinâmica de Newton.
e) a grandeza viscosidade no princípio de Arquimedes.
4.
A figura foi obtida em uma câmara de nuvens, equipamento que registra trajetórias
deixadas por partículas eletricamente carregadas. Na figura, são mostradas as trajetórias dos
produtos do decaimento de um isótopo do hélio ( 62 He) em repouso: um elétron (e ) e um
isótopo de lítio ( 63 Li), bem como suas respectivas quantidades de movimento linear, no
instante do decaimento, representadas, em escala, pelas setas. Uma terceira partícula,
denominada antineutrino (ν carga zero), é também produzida nesse processo.
O vetor que melhor representa a direção e o sentido da quantidade de movimento do
antineutrino é:
a)
b)
c)
d)
e)
5. A figura mostra uma colisão envolvendo um trem de carga e uma camionete. Segundo
testemunhas, o condutor da camionete teria ignorado o sinal sonoro e avançou a cancela da
passagem de nível.
Após a colisão contra a lateral do veículo, o carro foi arrastado pelo trem por cerca de 300
metros. Supondo a massa total do trem de 120 toneladas e a da camionete de 3 toneladas,
podemos afirmar que, no momento da colisão, a intensidade da força que:
a) o trem aplicou na camionete foi 40 vezes maior do que a intensidade da força que a
camionete aplicou no trem e a colisão foi parcialmente elástica.
b) o trem aplicou na camionete foi 40 vezes maior do que a intensidade da força que a
camionete aplicou no trem e a colisăo foi inelástica.
c) a camionete aplicou no trem foi igual à intensidade da força que o trem aplicou na camionete
e a colisão foi parcialmente elástica.
d) a camionete aplicou no trem foi igual à intensidade da força que o trem aplicou na camionete
e a colisão foi inelástica.
6. Uma balsa de 2,00 toneladas de massa, inicialmente em repouso, transporta os carros A e
B, de massas 800 kg e 900 kg, respectivamente. Partindo do repouso e distantes 200 m
inicialmente, os carros aceleram, um em direção ao outro, até alcançarem uma velocidade
constante de 20 m s em relação à balsa. Se as acelerações são a A  7,00 m s2
e
aB  5,00 m s2 , relativamente à balsa, a velocidade da balsa em relação ao meio líquido, em
m s, imediatamente antes dos veículos colidirem, é de:
a) zero
b) 0,540
c) 0,980
d) 2,35
e) 2,80
7. Os Jogos Olímpicos de 2016 (Rio 2016) é um evento multiesportivo que acontecerá no Rio
de Janeiro. O jogo de tênis é uma das diversas modalidades que compõem as Olímpiadas. Se
em uma partida de tênis um jogador recebe uma bola com velocidade de 18,0 m s e rebate na
mesma direção e em sentido contrário com velocidade de 32 m s, assinale a alternativa que
apresenta qual o módulo da sua aceleração média, em m s2 , sabendo que a bola
permaneceu 0,10 s em contato com a raquete.
a) 450.
b) 600.
c) 500.
d) 475.
e) 200.
8. Um torcedor de futebol, durante uma partida do campeonato brasileiro de 2015, resolveu
utilizar seus conhecimentos de Física para explicar diversas jogadas.
Nesta perspectiva, leia com atenção as afirmações a seguir e marque V para as verdadeiras e
F para as falsas:
(
) A força que o jogador exerce sobre a bola, ao chutá-la, é maior do que a força que a bola
exerce sobre o pé do jogador.
(
) A energia cinética da bola em movimento é diretamente proporcional ao quadrado da sua
velocidade.
(
) Se, em uma determinada jogada da partida, a bola cair verticalmente de uma altura, a
energia potencial em relação a Terra será diretamente proporcional ao quadrado da altura.
( ) Na cobrança de um pênalti, o jogador altera a quantidade de movimento da bola, que, por
sua vez, é novamente alterada quando a bola se choca com a rede.
Assinale a opção que contém a sequência CORRETA das respostas, de cima para baixo:
a) F, V, V, V.
b) V, F, F, V.
c) F, V, F, V.
d) F, F, V, V.
e) V, V, V, F.
9. “Ao utilizar o cinto de segurança no banco de trás, o passageiro também está protegendo o
motorista e o carona, as pessoas que estão na frente do carro. O uso do cinto de segurança no
banco da frente e, principalmente, no banco de trás pode evitar muitas mortes. Milhares de
pessoas perdem suas vidas no trânsito, e o uso dos itens de segurança pode reduzir essa
estatística. O Brasil também está buscando, cada vez mais, fortalecer a nossa ação no campo
da prevenção e do monitoramento. Essa é uma discussão que o Ministério da Saúde vem
fazendo junto com outros órgãos do governo”, destacou o Ministro da Saúde, Arthur Chioro.
Estudo da Associação Brasileira de Medicina de Tráfego (Abramet) mostra que o cinto de
segurança no banco da frente reduz o risco de morte em 45% e, no banco traseiro, em até
75%. Em 2013, um levantamento da Rede Sarah apontou que 80% dos passageiros do
banco da frente deixariam de morrer, se os cintos do banco de trás fossem usados com
regularidade.
Em uma colisão frontal, um passageiro sem cinto de segurança é arremessado para a frente.
Esse movimento coloca em risco a vida dos ocupantes do veículo. Vamos supor que um carro
popular com lotação máxima sofra uma colisão na qual as velocidades inicial e final do veículo
sejam iguais a 72 km h e zero, respectivamente. Se o passageiro do banco de trás do veículo
tem massa igual a 80 kg e é arremessado contra o banco da frente, em uma colisão de
400 ms de duração, a força média sentida por esse passageiro é igual ao peso de:
a) 360 kg na superfície terrestre.
b) 400 kg na superfície terrestre.
c) 1440 kg na superfície terrestre.
d) 2540 kg na superfície terrestre.
e) 2720 kg na superfície terrestre.
10.
O pêndulo balístico, inventado no século XIX, é um dispositivo bastante preciso na
determinação da velocidade de projéteis e é constituído por um bloco, geralmente de madeira,
suspenso por dois fios de massas desprezíveis e inextensíveis, conforme mostrado a seguir.
Para o pêndulo da figura, considere que o projétil tenha massa de 50 g e o bloco de 5 kg e
que, após ser atingido pelo projétil, o bloco alcança uma altura h  20 cm. Determine a
velocidade do projétil no instante em que atinge o bloco. (Faça g  10 m s2 ).
a) 202 m s.
b) 212 m s.
c) 222 m s.
d) 242 m s.
e) 252 m s.
11. Tempestades solares são causadas por um fluxo intenso de partículas de altas energias
ejetadas pelo Sol durante erupções solares. Esses jatos de partículas podem transportar
bilhões de toneladas de gás eletrizado em altas velocidades, que podem trazer riscos de danos
aos satélites em torno da Terra.
Considere que, em uma erupção solar em particular, um conjunto de partículas de massa total
mp  5 kg, deslocando-se com velocidade de módulo vp  2  105 m / s, choca-se com um
satélite de massa Ms  95 kg que se desloca com velocidade de módulo igual a
Vs  4  103 m / s na mesma direção e em sentido contrário ao das partículas. Se a massa de
partículas adere ao satélite após a colisão, o módulo da velocidade final do conjunto será de:
a) 102.000 m / s.
b) 14.000 m / s.
c) 6.200 m / s.
d) 3.900 m / s.
12. O trilho de ar é um dispositivo utilizado em laboratórios de física para analisar movimentos
em que corpos de prova (carrinhos) podem se mover com atrito desprezível. A figura ilustra um
trilho horizontal com dois carrinhos (1 e 2) em que se realiza um experimento para obter a
massa do carrinho 2. No instante em que o carrinho 1, de massa 150,0 g, passa a se mover
com velocidade escalar constante, o carrinho 2 está em repouso. No momento em que o
carrinho 1 se choca com o carrinho 2, ambos passam a se movimentar juntos com velocidade
escalar constante. Os sensores eletrônicos distribuídos ao longo do trilho determinam as
posições e registram os instantes associados à passagem de cada carrinho, gerando os dados
do quadro.
Carrinho 1
Carrinho 2
Posição (cm)
Instante (s)
Posição (cm)
Instante (s)
15,0
0,0
45,0
0,0
30,0
1,0
45,0
1,0
75,0
8,0
75,0
8,0
90,0
11,0
90,0
11,0
Com base nos dados experimentais, o valor da massa do carrinho 2 é igual a:
a) 50,0 g.
b) 250,0 g.
c) 300,0 g.
d) 450,0 g.
e) 600,0 g.
Dois caminhões de massa m1  2,0 ton e m2  4,0 ton, com velocidades v1  30 m / s e
v2  20 m / s, respectivamente, e trajetórias perpendiculares entre si, colidem em um
cruzamento no ponto G e passam a se movimentar unidos até o ponto H, conforme a figura
abaixo. Considerando o choque perfeitamente inelástico, o módulo da velocidade dos veículos
imediatamente após a colisão é:
13.
a) 30 km / h
b) 40 km / h
c) 60 km / h
d) 70 km / h
e) 75 km / h
14. Para responder à questão, analise a situação a seguir.
Duas esferas – A e B – de massas respectivamente iguais a 3 kg e 2 kg estão em movimento
unidimensional sobre um plano horizontal perfeitamente liso, como mostra a figura 1.
Inicialmente as esferas se movimentam em sentidos opostos, colidindo no instante t1. A figura
2 representa a evolução das velocidades em função do tempo para essas esferas
imediatamente antes e após a colisão mecânica.
Sobre o sistema formado pelas esferas A e B, é correto afirmar:
a) Há conservação da energia cinética do sistema durante a colisão.
b) Há dissipação de energia mecânica do sistema durante a colisão.
c) A quantidade de movimento total do sistema formado varia durante a colisão.
d) A velocidade relativa de afastamento dos corpos após a colisão é diferente de zero.
e) A velocidade relativa entre as esferas antes da colisão é inferior à velocidade relativa entre
elas após colidirem.
15. Em um dado jogo de sinuca, duas das bolas se chocam uma contra a outra. Considere
que o choque é elástico, a colisão é frontal, sem rolamento, e despreze os atritos. No sistema
composto pelas duas bolas há conservação de:
a) momento linear e força.
b) energia cinética e força.
c) momento linear e energia cinética.
d) calor e momento linear.
16. Em um experimento utilizando bolas de bilhar, uma bola A é arremessada com velocidade
horizontal de módulo v A , em uma superfície horizontal fixa e sem atrito. A bola A colide
elasticamente com outra bola idêntica, B. Sobre o movimento do centro de massa do conjunto
de bolas, sabendo que a bola B está sempre em contato com a superfície, assinale a
alternativa CORRETA.
a) Permanece em repouso, durante o movimento de A e B na plataforma.
b) Permanece em repouso, durante o movimento na rampa da partícula B.
c) Está em movimento uniformemente variado, antes da colisão.
d) Está em movimento uniforme, depois da colisão, enquanto B ainda está na plataforma.
e) Está em movimento uniforme, durante o movimento descendente da partícula B.
17. Uma bola feita com massa de modelar, realizando movimento retilíneo uniforme, colide
frontalmente com outra bola de mesmo material que estava em repouso. Após a colisão, as
duas bolas permanecem unidas enquanto se movem. Considere que as bolas formam um
sistema de corpos isolados e o movimento ocorre todo em uma única direção. As alternativas a
seguir mostram o comportamento da energia cinética (Ec ) do sistema de corpos antes e
depois da colisão.
Assinale a alternativa que corresponde à colisão descrita.
a)
b)
c)
d)
e)
18. O airbag e o cinto de segurança são itens de segurança presentes em todos os carros
novos fabricados no Brasil. Utilizando os conceitos da Primeira Lei de Newton, de impulso de
uma força e variação da quantidade de movimento, analise as proposições.
I. O airbag aumenta o impulso da força média atuante sobre o ocupante do carro na colisão
com o painel, aumentando a quantidade de movimento do ocupante.
II. O airbag aumenta o tempo da colisão do ocupante do carro com o painel, diminuindo assim
a força média atuante sobre ele mesmo na colisão.
III. O cinto de segurança impede que o ocupante do carro, em uma colisão, continue se
deslocando com um movimento retilíneo uniforme.
IV. O cinto de segurança desacelera o ocupante do carro em uma colisão, aumentando a
quantidade de movimento do ocupante.
Assinale a alternativa correta.
a) Somente as afirmativas I e IV são verdadeiras.
b) Somente as afirmativas II e III são verdadeiras.
c) Somente as afirmativas I e III são verdadeiras.
d) Somente as afirmativas II e IV são verdadeiras.
e) Todas as afirmativas são verdadeiras.
19.
Uma massa de 10 g e velocidade inicial de 5,0 m / s colide, de modo totalmente
inelástico, com outra massa de 15 g que se encontra inicialmente em repouso.
O módulo da velocidade das massas, em m/s, após a colisão é:
a) 0,20
b) 1,5
c) 3,3
d) 2,0
e) 5,0
20. Dois estudantes da FGV divertem-se jogando sinuca, após uma exaustiva jornada de
estudos. Um deles impulsiona a bola branca sobre a bola vermelha, idênticas exceto pela cor,
inicialmente em repouso. Eles observam que, imediatamente após a colisão frontal, a bola
branca para e a vermelha passa a se deslocar na mesma direção e no mesmo sentido da
velocidade anterior da bola branca, mas de valor 10% menor que a referida velocidade. Sobre
esse evento, é correto afirmar que houve conservação de momento linear do sistema de bolas,
mas sua energia mecânica diminuiu em:
a) 1,9%.
b) 8,1%.
c) 10%.
d) 11,9%.
e) 19%.
21. Uma partícula de massa m se move com velocidade de módulo v imediatamente antes
de colidir elasticamente com uma partícula idêntica, porém em repouso. A força de contato
entre as partículas que atua durante um breve período de tempo T está mostrada no gráfico a
seguir.
Desprezando os atritos, determine o valor máximo assumido pela força de contato F0 :
a) 4mv / 3T
b) 2mv / 3T
c) mv / T
d) mv / 3T
e) mv / 4T
Considere duas rampas A e B, respectivamente de massas 1kg e 2 kg, em forma de
quadrantes de circunferência de raios iguais a 10 m, apoiadas em um plano horizontal e sem
atrito. Duas esferas 1 e 2 se encontram, respectivamente, no topo das rampas A e B e são
abandonadas, do repouso, em um dado instante, conforme figura abaixo.
22.
Quando as esferas perdem contato com as rampas, estas se movimentam conforme os
gráficos de suas posições x, em metros, em função do tempo t, em segundos, abaixo
representados.
Desprezando qualquer tipo de atrito, a razão
m1
das massas m1 e m2 das esferas 1 e 2,
m2
respectivamente, é:
1
a)
2
b) 1
c) 2
3
d)
2
23. A figura a seguir ilustra uma visão superior de uma mesa de sinuca, onde uma bola de
massa 400 g atinge a tabela com um ângulo de 60 com a normal e ricocheteia formando o
mesmo ângulo com a normal. A velocidade da bola, de 9 m / s, 9 m/s, altera apenas a direção
do movimento durante o choque, que tem uma duração de 10 ms.
A partir da situação descrita acima, a bola exerce uma força média na tabela da mesa de:
a) 360 N.
b) 5400 N.
c) 3600 N.
d) 4000 N.
e) 600 N.
24. Enquanto movia-se por uma trajetória parabólica depois de ter sido lançada obliquamente
e livre de resistência do ar, uma bomba de 400 g explodiu em três partes, A, B e C, de
massas mA  200 g e mB  mC  100 g. A figura representa as três partes da bomba e suas
respectivas velocidades em relação ao solo, imediatamente depois da explosão.
Analisando a figura, é correto afirmar que a bomba, imediatamente antes de explodir, tinha
velocidade de módulo igual a:
a) 100 m / s e explodiu antes de atingir a altura máxima de sua trajetória.
b) 100 m / s e explodiu exatamente na altura máxima de sua trajetória.
c) 200 m / s e explodiu depois de atingir a altura máxima de sua trajetória.
d) 400 m / s e explodiu exatamente na altura máxima de sua trajetória.
e) 400 m / s e explodiu depois de atingir a altura máxima de sua trajetória.
25. Um projétil de massa m  10,0 g viaja a uma velocidade de 1,00 km s e atinge um bloco
de madeira de massa M  2,00kg, em repouso, sobre uma superfície sem atrito, conforme
mostra a figura.
Considerando-se que a colisão entre o projétil e o bloco seja perfeitamente inelástica e
desprezando-se todas as forças resistivas, o valor aproximado da distância d percorrida pelo
bloco sobre a rampa, em metros, é:
a) 1,25.
b) 1,50.
c) 2,00.
d) 2,50.
e) 3,00.
26. Um artefato explosivo é lançado do solo com velocidade inicial v0 fazendo um ângulo de
30 com a horizontal. Após 3,0 segundos, no ponto mais alto de sua trajetória, o artefato
explode em duas partes iguais, sendo que uma delas (fragmento A) sofre apenas uma inversão
no seu vetor velocidade. Desprezando a resistência do ar, qual a distância, em metros, entre os
dois fragmentos quando o fragmento A atingir o solo?
sen30  0,5
Dados: cos30  0,9
g  10m s2
a)
b)
c)
d)
e)
280
350
432
540
648
27. Uma esfera de massa m é lançada do solo verticalmente para cima, com velocidade inicial
V, em módulo, e atinge o solo 1 s depois. Desprezando todos os atritos, a variação no
momento linear entre o instante do lançamento e o instante imediatamente antes do retorno ao
solo é, em módulo:
a) 2mV.
b) mV.
c) mV2/2.
d) mV/2.
28. Um bloco de massa M=180 g está sobre urna superfície horizontal sem atrito, e prende-se
a extremidade de uma mola ideal de massa desprezível e constante elástica igual a
2  103 N / m. A outra extremidade da mola está presa a um suporte fixo, conforme mostra o
desenho. Inicialmente o bloco se encontra em repouso e a mola no seu comprimento natural,
Isto é, sem deformação.
Um projétil de massa m=20 g é disparado horizontalmente contra o bloco, que é de fácil
penetração. Ele atinge o bloco no centro de sua face, com velocidade de v=200 m/s. Devido ao
choque, o projétil aloja-se no interior do bloco. Desprezando a resistência do ar, a compressão
máxima da mola é de:
a) 10,0 cm
b) 12,0 cm
c) 15,0 cm
d) 20,0 cm
e) 30,0 cm
29. O pêndulo de Newton pode ser constituído por cinco pêndulos idênticos suspensos em um
mesmo suporte. Em um dado instante, as esferas de três pêndulos são deslocadas para a
esquerda e liberadas, deslocando-se para a direita e colidindo elasticamente com as outras
duas esferas, que inicialmente estavam paradas.
O movimento dos pêndulos após a primeira colisão está representado em:
a)
b)
c)
d)
e)
30. Em uma mesa de sinuca, uma bola é lançada frontalmente contra outra bola em repouso.
Após a colisão, a bola incidente para e a bola alvo (bola atingida) passa a se mover na mesma
direção do movimento da bola incidente. Supondo que as bolas tenham massas idênticas, que
o choque seja elástico e que a velocidade da bola incidente seja de 2 m/s, qual será, em m/s, a
velocidade inicial da bola alvo após a colisão?
a) 0,5
b) 1
c) 2
d) 4
e) 8
31. Uma bomba é arremessada, seguindo uma trajetória parabólica, conforme representado
na figura abaixo. Na posição mais alta da trajetória, a bomba explode.
Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem
em que aparecem.
A explosão da bomba é um evento que __________ a energia cinética do sistema. A trajetória
do centro de massa do sistema constituído pelos fragmentos da bomba segue __________.
a) não conserva – verticalmente para o solo
b) não conserva – a trajetória do fragmento mais massivo da bomba
c) não conserva – a mesma parábola anterior à explosão
d) conserva – a mesma parábola anterior à explosão
e) conserva – verticalmente para o solo
32. A hipótese mais aceita nos meios científicos atribui a grande extinção da fauna terrestre,
ocorrida há aproximadamente 65 milhões de anos, à colisão de um corpo celeste de grandes
dimensões, possivelmente um cometa, com a superfície da Terra. Esse bólido foi absorvido
pela Terra e o que se seguiu foi um súbito desequilíbrio ambiental, que incluiu obstrução da
passagem da luz solar, maremotos e violentas erupções vulcânicas.
A respeito das propriedades desse tipo de colisão, complete as lacunas na afirmação a seguir.
Trata-se de um exemplo de choque perfeitamente __________, em que o momento linear do
sistema cometa-Terra __________ conservado. Nesse evento, ocorre __________ da energia
mecânica.
Assinale a sequência correta.
a) inelástico – é – conservação
b) elástico – não é – conservação
c) elástico – não é – dissipação
d) inelástico – não é – conservação
e) inelástico – é – dissipação
33. Uma experiência comum utilizando um acelerador de partículas consiste em incidir uma
partícula conhecida sobre um alvo desconhecido e, a partir da análise dos resultados do
processo de colisão, obter informações acerca do alvo. Um professor, para ilustrar de forma
simplificada como esse processo ocorre, propôs a seguinte situação em que uma partícula de
massa m1  0,2 kg colide com um alvo que inicialmente estava em repouso, conforme a figura.
Após a colisão, obteve-se como resultado que as componentes y das velocidades são
respectivamente v1y  5 m / s e v 2y  2 m / s. Neste caso, a massa do alvo em kg é:
a) 0,08
b) 0,2
c) 0,5
d) 0,8
e) 1,25
Gabarito:
Resposta
[E]
da
questão
1:
questão
2:
questão
3:
Qa  Qd
m  V  (m  M) 
V
M
 4  m  m  M  M  3m   3
4
m
Resposta
[A]
Δp  m  ΔV  Δp  50  103 
Resposta
[B]
da
108
 Δp  1,5 kg m s
3,6
da
Como a quantidade de movimento antes tem que ser igual à quantidade de movimento depois,
Qantes  Qdepois , o remador ao lançar o seu corpo para trás, ganha uma vantagem para cruzar
a linha de chegada.
Para entendermos melhor esse caso, podemos pensar em um vagão de trem, onde se
encontra uma pessoa. Digamos que o atrito entre o trilho e vagão seja desprezível, se uma
pessoa lançar uma pedra para trás, por conservação da quantidade de movimento o vagão irá
se movimentar para frente. A mesma coisa acontece com o remador que, ao lançar o corpo
para trás, ganha uma vantagem.
Resposta
[D]
da
questão
4:
A figura 1 mostra os vetores quantidade de movimento do elétron e do isótopo de lítio, bem
como a soma desses vetores.
Qe  QLi  Q1.
Como o isótopo de hélio estava inicialmente em repouso, a quantidade de movimento do
sistema era inicialmente nula. Como as forças trocadas entre as partículas emitidas no
decaimento são internas, trata-se de um sistema mecanicamente isolado, ocorrendo, então,
conservação da quantidade de movimento do sistema, que deve ser nula também no final.
 
Para satisfazer essa condição, o vetor quantidade de movimento do antineutrino Qν deve ter
mesma intensidade e sentido oposto à do vetor Q1, como também mostra a figura 1.
A figura 2 mostra a resolução usando a regra da poligonal, sendo: Qe  QLi  Q ν  0.
Resposta
[D]
da
questão
5:
De acordo com a 3ª lei de Newton, à toda ação corresponde uma reação de igual intensidade,
mesma direção e sentido contrário. Com isso, a força aplicada na camionete pelo trem tem a
mesma intensidade que a força aplicada pela camionete sobre o trem. Além disso, tendo em
vista que os dois móveis após a colisão andarem juntos, se trata de uma colisão inelástica,
confirmando a alternativa [D] como a correta.
Resposta
[B]
da
questão
6:
Primeiramente, fazendo a conferência do tempo para atingir a velocidade terminal e a distância
percorrida por cada carro, temos:
Para o carro A:
Δv A
20m s
Δt A 
 Δt A 
 Δt A  2,8 s
aA
7m s2
a
7 m s2
2
2
ΔsA  A   t A   ΔsA 
  2,8   ΔsA  28,6 m
2
2
Para o carro B:
Δv
20 m / s
ΔtB  B  ΔtB 
 ΔtB  4 s
aB
5 m s2
a
5 m s2
2
2
ΔsB  B   tB   ΔsB 
  4   ΔsB  40 m
2
2
Como as distâncias percorridas somadas não ultrapassam o comprimento da balsa, os dois
móveis se chocam com a velocidade de 20 m s em relação à balsa e em sentidos contrários.
Ao colidirem, temos a conservação da quantidade de movimento do sistema balsa e carros,
portanto:
Qf  Qi
Considerando como positivo o movimento do carro de maior massa e desprezando os efeitos
dos atritos, para o choque inelástico, temos:
mbalsa  mA  mB   v  mA  v A  mB  vB
v
mA  v A  mB  vB
800 kg  ( 20 m s)  900 kg  20 m s
v
 2000 kg  800 kg  900 kg
mbalsa  mA  mB 
E, finalmente, a velocidade final da balsa será:
18000  16000 kg  m s
v
 v  0,54 m s no mesmo sentido do carro B.
3700 kg
Resposta
[C]
a
da
questão
7:
Δv
32  ( 18)
50
a
a
 500 m s2
Δt
0,1
0,1
Ou usando o teorema do Impulso – Quantidade de movimento
F  Δt  m  Δv
m  a  Δt  m  Δv
m  a  Δt m  Δv

m
m
a  Δt  Δv
Δv
32  ( 18)
50
a
a
a
 500 m s2
Δt
0,1
0,1
Resposta
[C]
da
questão
8:
[F] A força que o jogador exerce sobre a bola, ao chutá-la, tem a mesma intensidade à da força
que a bola aplica no pé do jogador (Princípio da Ação-Reação).
m
[V] Ecin   v 2.
2
[F] Se em uma determinada jogada da partida, a bola cair verticalmente de uma altura, a
energia potencial em relação a Terra será diretamente proporcional à altura.
Epot  m  g  h.
[V] A cada choque ocorre variação na velocidade, ocorrendo variação na quantidade de
movimento.
Resposta
[B]
da
questão
9:
Transformando a velocidade e o tempo para o Sistema Internacional de unidades:
1m / s
vi  72km / h 
 20 m / s
3,6 km / h
Δt  400 ms 
1s
 0,4 s
1000 ms
Utilizando a definição de impulso e o teorema do impulso, têm-se a relação entre a força média
e a variação da quantidade de movimento:
ΔQ m   v f  vi 
I  ΔQ  Fm  Δt  Fm 

Δt
Δt
80 kg   0  20 m / s 
Fm 
 Fm  4000 N
0,4 s
E essa força média equivale a uma massa no campo gravitacional terrestre de:
F
4000 N
m m m
 m  400 kg
g
10 m / s2
Resposta
[A]
da
questão
10:
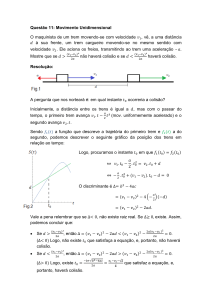
da
questão
11:
Ec  Ep
1
mv '2  mgh
2
1 2
v '  gh
2
v '  2gh  v '  2  10  0,2
v'  4  v'  2 m / s
Qa  Qd
mp  vp  mb  vb  (mb  mp )  v '
50v p  0  5.050  2
vp 
10.100
 v p  202 m / s
50
Resposta
[C]
Adotando como positivo o sentido do movimento do conjunto de partículas, temos os seguintes
dados:
mp  5 kg; vp  2  105 m/s; Ms  95 kg; VS   4  103 m/s.
Como se trata de um sistema mecanicamente isolado, ocorre conservação da quantidade de
movimento do sistema. Então:


depois
Qantes
mp vp  Ms Vs  mp  Ms V ' 
sist  Qsist
5  2  105  95    4  10
3
 100  V'  V ' 
100  104  38  104
 62  102 
100
V '  6.200 m/s.
Resposta
[C]
da
questão
12:
A velocidade do carrinho 1 antes do choque é:
Δs
30,0  15,0
v1  1 
 v1  15,0 cm s.
Δt1
1,0  0,0
O carrinho 2 está em repouso: v2  0.
Após a colisão, os carrinhos seguem juntos com velocidade v12, dada por:
v12 
Δs12 90,0  75,0

 v12  5,0 cm s.
Δt12
11,0  8,0
Como o sistema é mecanicamente isolado, ocorre conservação da quantidade de movimento.
depois
Qantes
 Q1 Q2  Q12  m1 v1  m2 v 2  (m1  m2 )v12 
sist  Qsist
150,0  15,0  (150,0  m2 )5,0  m2 
Resposta
[C]
da
150,0  15,0
 150,0 
5,0
m2  300,0 g.
questão
13:
Para esta análise, é necessário analisar as quantidades de movimento dos dois caminhões
vetorialmente, conforme figura abaixo.
Assim, temos que,
Qf  Q12  Q22
Qf 
m1  v1 2  m2  v 2 2
Qf 
 2000  30 2   4000  20 2
Qf 
 60000 2   80000 2
Qf  100  103 kg  m s
Assim, é possível encontrar a velocidade dos dois caminhões após a colisão.
Qf  m  v f
vf 
vf 
Qf
m1  m2 
100  103
6  103
100
vf 
ms
6
ou
v f  60 km h
Resposta
[B]
da
questão
14:
Pela análise do gráfico, constata-se que os corpos andam juntos após o choque (velocidade
relativa de afastamento dos corpos depois do choque é igual a zero), representando um
choque perfeitamente inelástico. Neste caso, a energia cinética não é conservada e existe a
perda de parte da energia mecânica inicial sob a forma de calor (energia dissipada) com
aumento da energia interna e temperatura devido à deformação sofrida no choque. Sendo
assim, a única alternativa correta é da letra [B].
Resposta
[C]
da
questão
Em uma colisão elástica conservam-se o momento linear e a energia cinética.
15:
Resposta
[D]
da
questão
16:
Antes e depois da colisão o centro de massa do conjunto de bolas possui o movimento
uniforme enquanto estão na plataforma, primeiramente aproximando-se da bola B e, finalmente
afastando-se. Na rampa passa a agir o campo gravitacional que irá acelerar as bolas, portanto
por eliminação chegamos à alternativa correta, letra [D].
Resposta
[A]
da
questão
17:
Como o movimento é retilíneo uniforme a aceleração é nula. Logo, a velocidade é constante.
1
Analisando a equação da energia cinética, Ec  mv 2 , percebemos que a velocidade e a
2
massa são diretamente proporcionais a Ec .
Pela lei de conservação de movimento vantes  v depois , logo, Ec
 Ec
.
antes
Resposta
[B]
da
questão
depois
18:
[I] Falsa. O airbag reduz a força média sobre o corpo do ocupante do carro durante a colisão
com o painel, pois aumenta o tempo de contato entre o sistema corpo-airbag. O impulso
permanece o mesmo, que equivale à diferença de quantidade de movimento.
[II] Verdadeira.
[III] Verdadeira.
[IV] Falsa.O cinto de segurança prende o passageiro ao banco evitando que o movimento do
seu corpo continue por inércia após o choque. A aceleração e a variação da quantidade de
movimento dos ocupantes que utilizam o cinto de segurança serão as mesmas sofridas pelo
automóvel no momento do acidente.
Resposta
[D]
da
questão
19:
As colisões totalmente inelásticas ocorrem quando os corpos após colidirem ficam unidos como
se fosse um só corpo e suas velocidades finais são iguais entre si.
A quantidade de movimento Q se conserva, portanto a quantidade de movimento antes da
colisão é a mesma após a colisão.
Qinicial  Qfinal
m1  v1  m2  v 2   m1  m2   v f
vf 
m1  v1  m2  v 2
m1  m2
Substituindo os valores:
10 g  5m / s  15 g  0m / s 50 g  m / s
vf 

 2m/s
10 g  15 g
25 g
Resposta
[E]
da
questão
20:
Calculando-se as energias cinéticas no momento antes e depois da colisão teremos:
Eci 
m  v 02
2
e
m   0,9  v0 
2
Ec f 
2
 0,81
m  v 02
 0,81 Eci
2
Assim, a perda de energia percentual pode ser calculada.
 Ec 
 0,81 Ec 
i
  100%
Perda   1  f   100%   1 



Ec 
Ec
i 
i



Perda  1  0,81  100%
Perda  19%
Resposta
[A]
da
questão
21:
Como o choque é elástico entre partículas de mesma massa, se as duas partículas se
encontrarem no alinhamento do centro de massa de ambas, elas trocam de velocidades.
Através do cálculo da área sob a curva do gráfico, temos o Impulso:
I  A1  A2  T 
F0 T F0 3
 
  T  F0
2 2 2 4
Pelo teorema do Impulso sabemos que I  ΔQ.
Para a partícula que se move durante o pequeno intervalo de tempo em que ocorre a interação
entre as duas partículas, a variação da quantidade de movimento é dada por:
ΔQ  m  v
Ficamos então com
3
mv   T  F0
4
E, finalmente:
4 mv
F0 
3 T
Resposta
[A]
da
questão
22:
Da figura, notamos que as duas esferas (1 e 2) possuem a mesma velocidade em módulo ao
final do trajeto curvilíneo, pois são lançadas de mesma altura.
Por conservação de energia em cada esfera:
v1  v 2  2Rg
Por conservação da quantidade de movimento nos conjuntos rampa e esfera:
m1v1  mA v A  1 v A (1)
m2v2  mBvB  2  vB (2)
Nota-se através do gráfico apresentado, que as duas rampas têm a mesma velocidade em
módulo, portanto v A  vB.
Sendo assim, a razão entre as massas das esferas 1 e 2 é dada por (1) dividido por (2):
m1 v1
1 v A

m2 v 2
2  vB
m1 1

m2 2
Resposta
[A]
da
questão
23:
Para a resolução da questão usaremos o teorema do Impulso
I  ΔQ (1)
Onde,
I  impulso da força média em N/s;
ΔQ  variação da quantidade de movimento em kg m/s que é calculada vetorialmente, como
vemos nas figuras:
ΔQ  Qf  Qi (2)
Nota-se que o triangulo formado é equilátero, pois todos os ângulos internos são iguais entre
si, sendo assim, a variação da quantidade de movimento ΔQ é exatamente igual à quantidade
de movimento inicial Qi e final Q f , isto é, em módulo
ΔQ  Qi  m  v  0,4kg  9
m
m
 3,6kg
s
s
Sabendo que o módulo do Impulso é dado por:
I  Fm  t (3)
Juntando as equações (3) e (1), temos:
Fm  t  ΔQ (4)
Donde sai a força média da colisão da bola com a tabela, em módulo:
ΔQ
3,6Ns
Fm 

 360N
t
10  103 s
Resposta
[B]
da
questão
24:
Dados: M  400 g; mA  200 g; mB  mC  100 g; v A  100 m/s; vB  200 m/s e vC  400 m/s.
Empregando a conservação da Quantidade de Movimento nas duas direções, para antes e
depois da explosão:
Na vertical (y):
Qantes
 Qdepois
 Qantes
 m B v B  m A v A  100  200  200  100 
y
y
y
Qantes
 0  a bomba explodiu no ponto mais alto de sua trajetória.
y
Na horizontal (x):
Qantes
 Qdepois
 M v 0  mC v C  400 v 0  100  400 
x
x
v 0  100 m/s.
Resposta
[D]
da
questão
25:
Em um sistema isolado, pode-se dizer que:
Qi  Qf
Desta forma, pode-se afirmar que a quantidade de movimento inicial é a soma da quantidade
de movimento do projétil mais a quantidade de movimento do bloco e a quantidade de
movimento final é o sistema projétil-bloco. Assim,
Qm  QM  QmM
m  vprojétil  M  vbloco  mTOTAL  v final
10  103  0  (2  0,01)  v final
v final 
v final
10
2,01
5m
s
Como não existem forças dissipativas, pode-se afirmar que a energia mecânica é conservada
durante o movimento. Desta forma,
Em  Em
i
f
mTOTAL  vi2
 mTOTAL  g  h
2
25
 10  h
2
h  1,25m
Assim, do triângulo, pode-se calcular a distância d percorrida:
sen  30  
h 1

d 2
d  2h
d  2,5m
Resposta
[E]
da
Baseado no que foi descrito no enunciado,
questão
26:
Na posição 1, o artefato é lançado do chão e o mesmo inicia sua trajetória de subida conforme
a linha tracejada da figura acima. No ponto mais alto de sua trajetória (onde existe somente a
componente horizontal da velocidade) o artefato é explodido, separando-o em duas parte
conforme posição 2, de forma que,
v a  v 0  cos  30 
Como o artefato leva 3 segundos para chegar a posição de altura máxima,
v y  v 0y  a  t
0  v 0y  ( 10)  3
v 0 y  30 m
s
Assim,
v0 
v 0y
sen(30)
v 0  60 m
s

30
0,5
Logo,
v a  60  0,9
v a  54 m
s
Para calcular a velocidade do fragmento B é preciso utilizar conceito de conservação de
quantidade de movimento.
m
m
m  v x   v a   vb
2
2
v  vb
vx  a
2
2  54   54   v b
vb  162 m
s
Como ambos os fragmentos irão demorar 3,0 segundos para descer até o chão,
Dist.  ΔSa  ΔSb  v a  t  vb  t
Dist.  54  3  162  3
Dist.  648 m
Resposta
[A]
da
questão
27:
Adotando o sentido positivo para baixo e trabalhando algebricamente, temos:
Lançamento : QL   m V
 ΔQ  QR  QL  m V    m V  

Re torno : QR  m V
ΔQ  2 m v .
Resposta
[D]
da
questão
Dados: M  180g  18  10 –2 kg; m  20g  2  10 –2 kg; k  2  10 –3 N / m; v  200m / s.
28:
Pela conservação da quantidade de movimento calculamos a velocidade do sistema (v s) depois
da colisão:
Qdepois
 Qantes

sist
sist
M  m vs  m v
 200 vs  20  200  v s  20 m/s.
Depois da colisão, o sistema é conservativo. Pela conservação da energia mecânica
calculamos a máxima deformação (x) sofrida pela mola.
inicial
EMec
final
 EMec
x  20 

M  m v 2s
18  2  102
3
2  10
2
 20 

k x2
2
20  102
2  10
3
 x  vs
 20  104
Mm
k

 x  20  102 m 
x  20 cm.
Resposta
[C]
da
questão
29:
Como se trata de sistema mecanicamente isolado, ocorre conservação da quantidade de
movimento.
Qfinal  Qincial  Qfinal  3 m v.
Portanto, após as colisões, devemos ter três esferas bolas com velocidade v como mostra a
alternativa [C].
Podemos também pensar da seguinte maneira: as esferas têm massas iguais e os choques
são frontais e praticamente elásticos. Assim, a cada choque, uma esfera para, passando sua
velocidade para a seguinte. Enumerando as esferas da esquerda para a direita de 1 a 5,
temos:
- A esfera 3 choca-se com a 4, que se choca com a 5. As esferas 3 e 4 param e a 5 sai com
velocidade v;
- A esfera 2 choca-se com a 3, que se choca com a 4. As esferas 2 e 3 param e a 4 sai com
velocidade v;
- A esfera 1 choca-se com a 2, que se choca com a 3. As esferas 1 e 2 param e a 3 sai com
velocidade v.
Resposta
[C]
da
questão
30:
Em choque frontal e perfeitamente elástico de dois corpos de mesma massa, eles trocam de
velocidades. Portanto, após o choque, se bola incidente para, a velocidade da bola alvo é 2
m/s.
Resposta
[C]
da
questão
31:
A energia não conserva, pois, durante a explosão, a queima da pólvora transforma energia
química em energia térmica e cinética, aumentando, então, a energia cinética do sistema.
Como as forças originadas na explosão são internas, não há alteração na trajetória do centro
de massa, que segue a mesma trajetória parabólica anterior à explosão.
Resposta
[E]
da
questão
32:
Trata-se de um exemplo de choque perfeitamente inelástico, pois o bólido ficou incrustado na
Terra. Sendo um sistema mecanicamente isolado, o momento linear (quantidade de
movimento) é conservado. Nesse evento, ocorre dissipação da energia mecânica.
Resposta
da
questão
33:
[C]
Como o movimento antes da colisão era estritamente sobre o eixo x, a componente da
quantidade de movimento no eixo y é nula. Pela conservação da quantidade de movimento
tem-se, então:
Qfinal
 Qinicial
 m1 v1y  m2 V2y  0  0,2  5  m2  2   0 
y
y
m2  0,5 kg.