ressonˆancia em circuito rlc-série - Feg

RESSONÂNCIA EM CIRCUITO RLC -SÉRIE
UNESP - Faculdade de Engenharia - Campus de Guaratinguetá
1
1. Introdução
Nesta prática vamos estudar a ressonância em um circuito RLC-série. Através das medições
da voltagem no resistor obteremos a curva de ressonância. Das caracterı́sticas desta curva determinaremos o valor dos parâmetros de elementos do circuito.
2. Fundamentos
Consideremos um capacitor carregado associado em série com um indutor com indutância L e
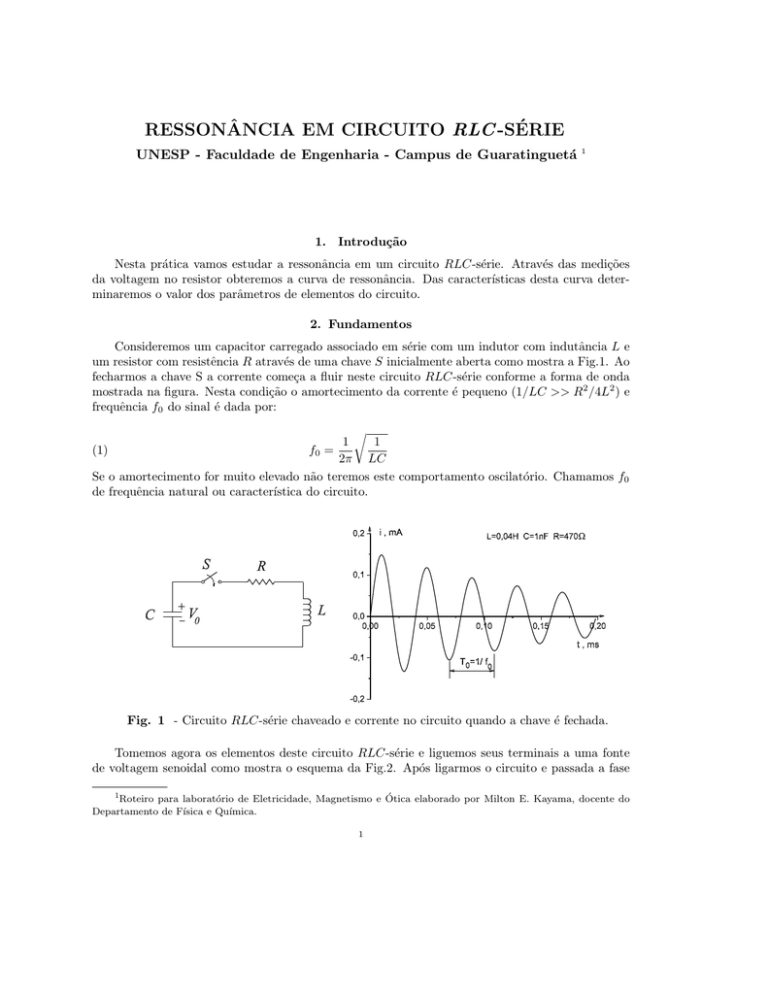
um resistor com resistência R através de uma chave S inicialmente aberta como mostra a Fig.1. Ao
fecharmos a chave S a corrente começa a fluir neste circuito RLC-série conforme a forma de onda
mostrada na figura. Nesta condição o amortecimento da corrente é pequeno (1/LC >> R2 /4L2 ) e
frequência f0 do sinal é dada por:
r
1
1
(1)
f0 =
2π LC
Se o amortecimento for muito elevado não teremos este comportamento oscilatório. Chamamos f0
de frequência natural ou caracterı́stica do circuito.
Fig. 1 - Circuito RLC-série chaveado e corrente no circuito quando a chave é fechada.
Tomemos agora os elementos deste circuito RLC-série e liguemos seus terminais a uma fonte
de voltagem senoidal como mostra o esquema da Fig.2. Após ligarmos o circuito e passada a fase
1
Roteiro para laboratório de Eletricidade, Magnetismo e Ótica elaborado por Milton E. Kayama, docente do
Departamento de Fı́sica e Quı́mica.
1
2
transiente, a corrente e a voltagem no circuito vão oscilar na frequência da fonte. A mesma corrente
flui através dos elementos. Vamos escrever esta corrente na forma:
(2)
i(t) = I0 senωt
onde I0 é a amplitude e ω = 2πf a frequência angular.
A impedância do resistor é ZR = R e sua voltagem, com
amplitude RI0 , está em fase com a corrente. No capacitor a
impedância é ZC = 1/(ωC) = XC e a voltagem, com amplitude XC I0 , está atrasada de π/2 rad em relação à corrente.
No indutor a impedância é ZL = ωL = XL e a voltagem,
com amplitude XL I0 , está adiantada de π/2 rad em relação
à corrente. As grandezas XC e XL são chamadas respectivamente de reatância capacitiva e reatância indutiva. As
voltagens no resistor, capacitor e indutor são portanto dadas
por:
(3)
(4)
(5)
Fig. 2 - Circuito RLC-série.
vR (t) = RI0 senωt
vC (t) = XC I0 sen(ωt − π/2)
vL (t) = XL I0 sen(ωt + π/2)
Daqui para frente, para simplificar, vamos omitir o tempo t na notação.
A voltagem totalpé v = vR + vC + vL . Usando as equações (3), (4), (5) e a identidade Rsenωt +
(XL − XC )cosωt = R2 + (XL − XC )2 sen[ωt + tg −1 (XL − XC )/R] obteremos:
(6)
v = V0 sen(ωt + θ)
onde
(7)
·
θ = tg
e
(8)
V0 =
p
−1
XL − XC
R
¸
R2 + (XL − XC )2 I0
A impedância Z do circuito é dada por Z = V0 /I0 ou:
(9)
Z=
p
R2 + (XL − XC )2
A variação da impedâncias, das reatâncias e da corrente com a frequência são mostradas na
Fig.3. Observamos máximos acentuados nos gráficos quando f = f0 . Esta é a condição quando
a frequência do sinal da fonte é igual à frequência caracterı́stica do circuito. Quando isto ocorre
dizemos que o circuito encontra-se √
em ressonância.
Na ressonância ω = ω0 = 1/ LC. Em consequência XL = XC e pela equação (9) temos
Z = R, ou seja, a impedância é mı́nima e igual a R. Ainda (a): pela equação (8) temos I0 = V0 /R,
ou seja, a amplitude da corrente é máxima;(b): pela equação (7) temos θ = 0, ou seja, a voltagem
e a corrente no circuito estão em fase; (c): pelas equações (4) e (5) temos que a amplitude da
voltagem no capacitor e no indutor são iguais embora defasadas entre si de π rad. Em consequência
a soma das voltagens nestes elementos é nula na ressonância e a voltagem total é igual à voltagem
no resistor.
2. FUNDAMENTOS
3
A potência instantânea dissipada no resistor é p = Ri2 = RI02 sen2 (ωt + θ). O valor médio é
< p >=< RI02 sen2 (ωt + θ) >= RI02 < sen2 (ωt + θ) >. Como < sen2 (ωt + θ) >= 1/2 teremos:
(10)
< p >=
RI02
RV02
=
2
2(R2 + (XL − XC )2 )
O gráfico de < p > é mostrado na Fig. 4, cuja curva apresenta um valor máximo na ressonância
(f = f0 ).
20
0,2
C
f
0
X
10
L
, mA
X
I
Z , k
15
I
L=0,04H
0,1
C=1 nF
Z
mx
R=4,7 k
5
0,70
R
f0
f1
f0
0
I
mx
f2
0,0
0
20
40
60
80
0
20
40
f , kHz
60
80
f , kHz
Fig. 3 - Variação da impedância Z e da amplitude I0 da corrente com a frequência.
< p > , unidade arbitrária
L=0,04 H
C=0,47 nF
4
V = 1 V
0
1/2
, mA
R= 220
Q=42
I
0
f
2
R=1200
1/2
f
0
f
1
20
0
f
Q=7,7
2
40
60
0
80
f , kHz
30
35
f
0
40
f , kHz
Fig. 4 - Potência dissipada no circuito.
Fig. 5 - Corrente para diferentes Q.
A largura de banda do circuito é o intervalo da frequência ∆f = f2 − f1 e é dada por:
(11)
∆f =
R
2πL
45
4
Corresponde
√ ao intervalo de frequência onde a amplitude da corrente situa-se entre o valor máximo
Imx e (1/ 2)Imx = 0, 70Imx , ou seja, entre a corrente máxima e 70% deste valor. Neste intervalo,
a potência média dissipada no circuito situa-se entre a potência máxima pmx = V02 /2R e 0, 5pmx ,
ou seja, entre a potência máxima e a metade deste máximo.
O fator de qualidade Q é definido por Q = ω(energia armazenada)/(potência média dissipada).
Neste circuito ela se reduz à forma:
2πf0 L
R
O fator Q é também Q = V0L /V0R = V0C /V0R onde V0L , V0R e V0C são respectivamente a voltagem
no indutor, no resistor e no capacitor na ressonância. Curvas tı́picas da corrente para diferentes
valores de Q são mostrados na Fig.5.
(12)
Q=
3. Prática
O objetivo é determinarmos a curva de ressonância da corrente (equação (8)) ou da potência
(equação (10)), conforme orientação do professor. Estas equações podem ser reescritas. Conforme a
equação (3) a amplitude da corrente I0 e a amplitude da voltagem V0R no resistor estão relacionadas
por I0 = V0R /R. Usando na equação da potência obtemos:
RI02
V2
= 0R
2
2R
Portanto em ambos os casos basta realizar medições de V0R , a voltagem no resistor.
(13)
< p >=
O circuito de medição é mostrado na Fig. 6.
O gerador de sinais usado para alimentar o circuito possibilita variarmos a frequência do sinal
senoidal e de sua amplitude. Os sinais da voltagem total e sobre o resistor mostrados na figura
serão medidos no osciloscópio.
Primeiro determine o perı́odo de ressonância
T0 = 1/f0 usando figuras de Lissajour. Na ressonância a defasagem entre a voltagem total e a
Fig. 6 - Montagem para medição.
corrente ( em fase com a voltagem no resistor) é
nula e a figura na tela será uma reta.
Conhecido o valor de f0 realize medições da voltagem no resistor V0R para outras frequências.
Mantenha a amplitude da voltagem V0 constante usando a regulagem disponı́vel no gerador de
função. Recomenda-se fazer o gráfico da curva ressonante no mesmo instante em que os dos dados
estão sendo coletados.
4. Prática
No relatório faça o gráfico da corrente ou da potência em função da frequência e obtenha ∆f
da curva de ressonância. A partir deste valor e da frequência de ressonância f0 obtenha os valores
de L e C supondo que o valor da resistência seja conhecido.