6 - Leis de Newton aplicadas aos fluidos 6.1 Noção básica de força

1 6 ‐ Leis de Newton aplicadas aos fluidos 6.1 Noção básica de força e fluxo de momento A segunda lei de Newton aplicada a uma certa massa M escreve‐se na forma mais básica na forma: F=M(dv/dt) =M a onde F é a resultante das forças, a=aceleração=derivada em ordem ao tempo da velocidade. Tal permite prever a aceleração como a=Dv/dt=F/M. Definindo momento linear ou quantidade de movimento como p=Mv =produto da massa pela velocidade, a 2ª lei de Newton reescreve‐se: dp/dt=F. No entanto a fórmula anterior pode assumir formas mais complicadas no casos seguintes: 1) A massa M do sistema variável, por exemplo ganhando ou perdendo massa através de 
caudais de entrada/saída. Representemos o caudal por dM / dt  m em kg/s, positivo se o sistema importar massa. 2) Existem fluxos de momento linear, isto é o sistema pode importar ou exportar partículas em movimento, isto é com velocidade vf não nula. Essa importação ou exportação, devida a caudais, fará aumentar ou diminuir a velocidade v do sistema produzindo uma aceleração. Tal é por exemplo a manifestação do ricochete de uma mangueira que expele água a elevada velocidade enquanto a mangueira recua. Representemos esse fluxo por Fp (em kg ms‐1/s ). Esse fluxo é dado por:  


Fp  m  v f  nint  onde v f é a velocidade do fluido segundo o eixo coordenado 
considerado e nint é o versor normal apontando para o interior no local do caudal. 3) A velocidade é medida num referencial acelerado com aceleração ar (e.g. um elevador em arranque ou em travagem), havendo por isso que incluir em F as forças aparentes na forma Fap   Mar . A taxa de variação do momento linear será devida à resultante F que será decomposta em força real (ex. peso, força de pressão, força aplicada) e força aparente (não nula só nos referenciais acelerados) e ao fluxo Fp de momento linear. A 2ª lei de Newton deverá ser reescrita na forma: 
 
dp d ( Mv)
dv


 F  Fp  Freal  Fap  Fp  M
 Freal  Fap  m v  m  v f  nint 
dt
dt
dt
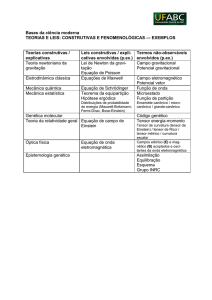
6.1 Assim a aceleração do sistema constituído de fluido será devida à soma de 4 termos: a força real, a força aparente, o caudal e o fluxo de momento linear. Para cada um dos 3 eixos coordenados escreve‐se uma equação escalar do momento. Além disso há que definir o referencial do movimento (inercial ou acelerado) e o volume de controle  sobre o qual se avaliam os fluxos de massa e momento. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 2 Vamos apresentar 4 casos simples em que dá enfâse a cada um desses termos. Consideremos um tanque de fluido com massa M e que está apoiado no solo. Em todas as situações a aceleração do tanque é nula M
dv
 0 . Pretende‐se avaliar a força aplicada em cada uma das dt
4 circunstâncias e que se representará por F1,F2,F3 e F4 respetivamente. Na situação 2 o referencial é acelerado para cima na direção y. Nas situações 3 e 4 há caudais positivo e negativo respetivamente. Em 3 a massa desloca‐se à velocidade constante v segundo x. Em 4 observa‐se um caudal de saída com velocidade vf contrária ao eixo y. As forças em 1,2,4 são as que seriam registadas numa balança de mola por baixo da massa. A força em 3 é a necessária para manter a velocidade v constante segundo x. A tabela resume os valores de todos os 4 termos da equação de Newton. mv  

m  v f  nint  0 0 F1  Mg 0 F2  Mg  Mar  F1 0 F3  m v 
1 Inercial y Fap dv Freal dt
0  Mg  F1 0 2 acelerado Y 0  Mg  F2  Mar 0 3 Inercial X 0 F3 4 Inercial Y 0  Mg  F4 0 Referencial eixo 0 
m v  0
0 Fi 



m0
F4  Mg  | m | v f  F1

 


v f   v f ey ; nint  ey  



m  v f  nint  | m | v f  0
Em 1, a força F1 equilibra o peso. Em 2, a força F2 é maior que o peso e equilibra o peso e a força aparente. Em 3, a força F3 é a necessária para manter a velocidade v constante, caso contrário esta iria decrescer por inercia. Em 4, a força F4 é menor que o peso dado que há um fluxo negativo de momento segundo ‐y ou o mesmo que fluxo positivo de momento segundo y. Esse fluxo atua como uma força de reação no sentido positivo de y aliviando o peso. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 3 A formulação anterior é essencial e necessária em fluidos dado que o escoamento produz transporte de massa (caudais) e fluxos de momento e energia, contrariamente aos sólidos ideais em que não há escoamento e o balanço de momento linear se resume a equilíbrios de forças reais e aparentes. Momento linear Em mecânica de fluidos é necessário ter em a conta a distribuição contínua da massa e por isso as grandezas extensivas vêm expressas como integrais ao longo de um certo volume de controle preenchido de fluido. Assim, consideremos um determinado volume de controle  ocupado por meio contínuo, eventualmente variável no tempo e limitado pela superfície fronteira . O momento linear ou quantidade de movimento é definido por: 
p  
 ( r ,t )

 v dv 6.2 O momento linear é uma grandeza extensiva com unidades SI (kg m s.1), cuja densidade 
mássica é a velocidade v das partículas. Desse modo é possível aplicar o teorema do 
transporte de Reynolds (5.20) com a densidade mássica genérica dada por v . Assim a taxa de geração de momento linear vem: 
dp

dt

Dv

dv

 ( r ,t )
Dt

Taxa de Geração Material de Momento
Linear




 
v  vsup

dnint  vrel  v ; vrel 

 ( r ,t )


Velocidade Relativa das
Fluxo Mássico Relativo de
MomentoLinear
partículasem relação à
superfície de controle
6.3
Tal é composto de 2 termos. O 2º termo de 6.3 é o fluxo de momento linear devido aos 
caudais de massa nas fronteiras abertas vrel  0 e corresponde ao termo de fluxo Fp da equação 6.1. Esse termo é nulo no caso de  ser um volume material no qual não há qualquer 

fluxo de massa dado que v  vsup na fronteira. O 1º termo de 6.3 é a geração material de 
momento linear e é igual à resultante F das forças aplicadas à matéria preenchida pelo volume  tal como em 6.1. Assim a 2ª lei de Newton aplicada a um volume de controle escreve‐se: 

dp



 F 
d



n
v
v
int
rel
 ( r ,t )
dt Resultante 
das forças
Fluxo Mássico Relativo de
MomentoLinear
Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6.4
4 Momento angular 

O momento angular H de uma massa pontual de vetor posição r , massa M e   

 
momento linear p é dado por H  r  p  Mr  v . O momento angular é relevante para 
caracterizar o movimento circular num plano perpendicular a um determinado versor e .   
Assim admitamos como hipótese que r , p  e ou seja que o vetor posição e a velocidade 
existem no plano perpendicular a e . Além disso, para o produto externo apenas contribui a 


projeção de v que é perpendicular a r , a qual representamos por v . Desse modo tem‐se: 



H  M r v e  I  e  H e ;
I  Mr 2  Momento de inércia
6.5
  v / r  velocidade angular ( 0 sentido direto)

Assim o momento angular segundo o versor e de um meio contínuo vem: 
H  
 ( r ,t )


 (r  v )  e dv  
 ( r ,t )
rv  dv

onde r  r
6.6
O momento angular assim calculado é relevante por exemplo para o cálculo do movimento de uma bomba rotativa impulsionada por fluido ou o movimento rotativo de um torniquete de rega ou uma turbomáquina em que pás com forma de hélice impulsionam fluido. Para calcular a taxa de variação do momento angular aplica‐se o teorema do transporte de 


Reynolds (5.20) com a densidade mássica a  (r  v )  e  rv .  
dH



M e

dnint  vrel  (rv )


(
r
,
t
)
Resultante
dt dos momentos
 das forças 
segundo o eixo de rotação
6.7
Fluxo Mássico Relativo de
Momento Angular pelas
fronteiras abertas
No caso de a força total ser um integral de forças volúmicas (distribuídas pelo volume), então 
Dv

dv . Desse modo A resultante dos momentos de força (torques ou binários)
 ( r ,t )
Dt


F  

f


M é o integral (soma) de todos os momentos das forças infinitesimais sendo f a densidade de força (N/kg). A resultante dos momentos é: 

Dv

 

r 
 
r  f  dv  rCF  F  ( r ,t )
 ( r ,t )
Dt


M  



f
Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6.8 5 
em que rCF é o centro de forças da resultante ou seja o ponto de aplicação no qual a força resultante produz o mesmo momento que a resultante de todos os momentos. Para cada tipo de força que compõe F, pode calcular‐se o respetivo centro de forças. Assim obtém‐se os centros de forças do peso (centro de massa), centro das forças de pressão etc. 
Se o momento angular tiver apenas componente segundo um versor e , então o momento de 
força também tem apenas componente segundo e ou seja: 

M  Me ; M  
 ( r ,t )
r f   dv  rCF F 
6.9 

onde f  e F são as projeções de f e F que são perpendiculares a r , contadas positivamente no sentido direto. Exemplo: Imaginemos um torniquete que roda em torno do fulcro O no plano vertical, expele fluido com caudal m’ à velocidade v no sentido direto, à distância R1 do fulcro. Tal provoca um fluxo negativo de momento angular. Para impedir o movimento do torniquete em sentido retrógrado (horário), deve esse fluxo ser equilibrado pelo momento de uma força F em sentido direto (positivo), aplicada à distância R2 do fulcro ou seja: 
0  FR2  m R1v 6.10 Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6 6.2 Forças aplicadas aos fluidos 
A resultante F das forças aplicadas a um volume de controle é um termo físico e resulta da soma de forças de várias naturezas, quer do ponto de vista físico (forças à distância como o peso, forças de pressão e atrito, forças de tensão superficial, forças pontuais etc.), quer do ponto de vista matemático, isto é as forças podem ser expressas como integrais de volume, superfície, de linha e ainda um simples vetor aplicado. No sentido de formalizar, consideremos de novo o volume de controle  sobre o qual se pretende calcular o balanço de momento linear. Esse volume está preenchido por meio contínuo (gás ou líquido) e eventualmente por paredes ou peças sólidas estáticas, móveis ou deformáveis, em contacto com o fluido (ex. a câmara cilíndrica onde funciona um piston de um motor de explosão a 4 tempos de um automóvel – figura). Esses componentes sólidos permitem conter o fluido num volume controlado (recipiente) ou então conforme o objetivo, podem ser movidos pelo fluido com o intuito de obter potência (e.g. aerogerador), ou então podem provocar o movimento do fluido através de forças exercidas por esses componentes sólidos (e.g. bomba de água, hélices de um barco, remo de um barco, asa de uma ave). O volume de controle  é descrito num referencial que em geral está associado a certos componentes sólidos que interagem com o fluido em estudo (e.g. fuselagem de um foguete expelindo gás a alta velocidade e que impele o foguete; corpo de uma ave). O volume pode ser fechado ou aberto permitindo a entrada ou a saída de fluido do interior do volume de controle através de tubos, canais abertos, válvulas, jatos livres sem canalização etc. A entrada e saída de massa permite exportar e importar consigo momento linear e outras propriedades extensivas tais como energia. O volume de controle  pode estar em repouso ou movimento uniforme (tal como num referencial inercial); pode também ter aceleração linear devido à aceleração da origem do referencial (e.g. um veículo de transporte de fluidos, sujeito a aceleração e descrito no referencial ligado ao veículo; um elevador em aceleração ascendente ou em travagem). O volume de controle  pode também ter aceleração angular devido à rotação do sistema de eixos cartesianos (e.g. balde com fluido em rotação; atmosfera e oceano sujeitos à rotação da Terra). Sempre que há aceleração linear ou angular do referencial, tal manifesta‐se na dinâmica do fluido sob a presença de forças aparentes que são incluídas na força resultante 
F . As superfícies limite de  podem separar meios contínuos homogéneos, constituídos pela mesma matéria (e.g superfície sólida imersa num fluido, i.e no interior do fluido) ou podem separar meios heterogéneos imiscíveis, constituídos por diferentes tipos de matéria (dois Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 7 líquidos imiscíveis; líquido e sólido; líquido e gás; gás e sólido). Qualquer uma dessas superfícies pode ser fixa ou móvel. No caso de uma das partes ser sólida, então a parte sólida pode controlar o movimento do fluido, fazendo‐o deslocar. Se ambas as partes forem fluidas (líquidos imiscíveis, e.g. água e azeite ou líquido e gás, tal como a superfície do mar), a superfície é livre, com movimento que não pode ser controlado exteriormente. As forças actuantes nas partículas de meio existentes no volume  podem ser resultantes da acção de campos de forças gravíticas (caso do peso, devido à atracção gravitacional terrestre e à força centrífuga associada à rotação da Terra), forças eléctricas sempre que as partículas de meio estejam electricamente carregadas na presença de um campo eléctrico e forças magnéticas sempre que as partículas estejam electricamente carregadas, em movimento e na presença de um campo magnético. As forças resultantes de campos de forças são proporcionais às densidades de massa e carga eléctrica e portanto escrevem‐se como integrais de volume de forças volúmicas. As forças volúmicas são de um modo geral proporcionais à massa expressando‐se em unidades de N/kg (newton por kilograma) ou ms‐2, que são as unidades SI de aceleração. As forças actuantes no meio resultam ainda de forças de coesão (entre moléculas idênticas) e adesão (entre moléculas distintas) que permitem que o meio mantenha uma certa forma, volume e estrutura. Essas forças intermoleculares são também conhecidas por forças de Van‐
der‐Waals. Se uma força for exercida por meio exterior a  ou na sua fronteira, a força é externa, se a força for exercida pelo meio existente no interior, a força diz‐se interna, como é o caso das forças de coesão e adesão. Pelo 3º Principio da mecânica de Newton (Lei da Acção‐Reacção que afirma que a uma força interna opõe‐se uma força interna simétrica), a resultante das forças internas apenas pode actuar sobre a superfície limite  de  e portanto a resultante é descrita como um integral de superfície em  de forças de superfície. Esse facto é devido à compensação entre forças internas. Essas forças internas são proporcionais à área do volume de controle. A força por unidade de área é a tensão, expressa no Sistema Internacional em N/m2=Pa (Newton por metro quadrado ou pascal). Se a força de superfície tiver uma componente que aponta para dentro de  (no sentido do versor normal interior), a força diz‐se de pressão, se a força tiver uma componente que aponta para fora, a força diz‐se de tensão ou tração. A parte da força que é tangente à superfície  diz‐se uma tensão de corte ou cisalhamento. As tensões normais ou seja perpendiculares à superfície existem em geral em todos os meios contínuos (sólidos ou fluidos) e traduzem as pressões existentes no seio do meio contínuo. A manifestação da força de pressão é evidente em muitas situações. Por exemplo num pneu cheio, a pressão interior é maior que a pressão atmosférica do exterior. A diferença (positiva) dessas pressões chama‐se pressão manométrica (pressão menos pressão atmosférica) que é medida nos manómetros de pressão. Ao desapertar a válvula do ar, a diferença de pressão interior e exterior cifra‐se numa força resultante que acelera o ar impelindo‐o para o exterior do pneu. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 8 Tensão superficial Consideremos a interface entre dois meios heterogéneos 1 e 2 (e.g. superfície livre de um líquido em contacto com outro líquido imiscível ou com um gás; superfície de contacto de um fluido com um sólido). Na linha de bordo L dessa interface existe uma força resultante das forças intermoleculares ou Van‐der‐Waals chamada de tensão superficial. (ver figura). A força de tensão superficial força Fts12 (em N) aplicada ao bordo L pela interface dos dois meios 1 e 2 é tangente à interface, perpendicular ao bordo L e aponta (puxa) na direção dos dois meios, isto é puxa o bordo L na direção dos meios 1 e 2. O versor 
tangente à interface e perpendicular a L, apontando para os meio é o versor u . A força é proporcional à extensão L (em m) e o coeficiente de proporcionalidade é a tensão superficial 12 (em N/m) que é característica do par de meios (1 e 2). 6.11 Por exemplo a tensão superficial água‐ar=0.072 N/m a 25ºC , decrescendo em geral com a temperatura. Geralmente a tensão superficial de um fluido é a referente à interface fluido‐ar. A força de tensão superficial pode ser medida através do seu equilíbrio com forças conhecidas. Por exemplo uma película líquida (ex. sabonária) retangular com largura b exerce uma força F=2L (devido às duas faces da película) sobre uma vareta sólida alinhada ao longo de b, com peso Mg. O equilíbrio de forças fornece 2b=F. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 9 A forma das gotas de um líquido (l) apoiado sobre um sólido (s), ambos expostos a um gás (g) (por exemplo ar), é determinada pelas forças de coesão (entre partículas líquidas) e de adesão (entre as líquidas e as outras sólidas e gasosas). O esquema mostra o perfil de uma gota que está em contacto com uma superfície sólida mostrando‐se as forças Flg , Fls, Fgs executadas sobre cada ponto do bordo pelas interfaces (líquido‐gás), (líquido‐sólido) e (gás‐sólido). O ângulo  chama‐se ângulo de ataque. Se <90º , o líquido ‘molha’ o sólido (exemplo: água sobre ferro) dada a elevada adesão do líquido ao sólido; se >90º, o líquido ‘não molha ou repele’ o sólido (exemplos: água sobre parafina ou mercúrio sobre vidro). As forças são proporcionais às respetivas tensões superficiais. O equilíbrio de forças segundo x conduz à lei de Young da tensão superficial:  ls
  lg cos    gs 6.12 A tensão superficial dos líquidos de densidade , é relevante apenas em fenómenos com uma escala espacial inferior ou da ordem do chamado comprimento de capilaridade: L 

g
6.13 No caso da água L=3 mm. O escoamento em tubos de diâmetro da ordem de L é muito influenciado pela tensão superficial (ex. vasos sanguíneos capilares). Um dos fenómenos da capilaridade é a forma do menisco (superfície livre do líquido num tubo capilar). O menisco pode ser côncavo com ascensão h de líquido ou pode ser convexo com rebaixamento h do líquido. O ângulo  que o líquido faz com o sólido do tubo capilar é o ângulo de ataque. Portanto a concavidade ou convexidade do menisco observa‐se se o tubo é molhável ou não. Admitindo um tubo circular de raio R, observa‐se o equilíbrio entre a força de tensão superficial e o peso da coluna de líquido de altura h (ou a ausência deste). Assim: Fts  2 R cos   ( R 2 h)  g  peso | h |
2 | cos  |
 gR
Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6.14 10 A tensão superficial é responsável por: 1) suspensão de pequenos objectos leves, mais densos que a água, sobre a superfície dos líquidos (e.g. agulhas metálicas, insetos), na figura anexa observa‐se a suspensão de um clip sobre a água devido às forças de tensão superficial ou capilares, a superfície comporta‐se como uma película elástica sujeita a uma certa tensão; 2) hidrofobia (repelência das gotas líquidas de uma superfície sólida impedindo que esta se molhe, como em certos tecidos); 3) capilaridade ou seja o movimento de líquidos no interior de tubos muito estreitos (e.g. vasos sanguíneos capilares); 4) Formação de bolhas de sabão e a esfericidade de gotas líquidas. As forças de tensão superficial exprimem‐se como integrais de linha (forças de linha) ao longo dos bordos das interfaces heterogéneas sendo proporcionais às extensões de linha e portanto medem‐se em N/m=Pa m (Pascal vezes metro). As forças de tensão superficial apenas podem provocar movimento e acelerações na película superficial dum líquido e não no interior do volume. Quando na superfície dum líquido há diferenças de tensão superficial, dá‐se movimento no sentido da menor para a maior tensão superficial. Esse movimento consiste no efeito Morongoni, responsável por exemplo do espraiamento de uma gota de álcool etílico sobre a água (http://www.youtube.com/watch?v=h7l4FeFJgbA&feature=related). Os líquidos que alteram a tensão superficial são chamados tensoativos ou surfatantes, tal como os detergentes. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 11 Expressão da Resultante de forças A força resultante aplicada a um volume de controle preenchido de meio contínuo é a soma de integrais de forças de várias naturezas (volume, superfície e linha), da resultante de forças aparentes em referenciais não inerciais (acelerados) e outras forças aplicadas não expressáveis de forma integral bem identificada (e.g. forças aplicadas por peças de máquinas e forças de reacção). A força resultante é: 





F    f dv    d     udl  Fnãoinerciais  Foutras


C
6.15
Na expressão anterior,  é o volume de controle sobre o qual atuam as forças volúmicas com 
f sendo a força por unidade de massa (com unidades N/kg), que multiplica pelo elemento de massa dv. Na superfície fronteira  do volume de controle atuam as forças de superfície 
com  sendo a força por unidade de superfície ou tensão (de unidade N/m2=Pa) que multiplica pelo elemento de superfície d. C é o conjunto de linhas sobre as quais actua a tensão superficial com  sendo a tensão superficial (em N/m) que multiplica pelo elemento de linha dl. A força de tensão superficial é tangencial à superfície de contacto dos meios heterogéneos 
aplicada para fora de C segundo o versor u , perpendicular ao bordo quer à (com bordo C), quer ao próprio bordo C (ver figura). Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 12 6.3 Forças volúmicas ou de volume Força volúmica Gravítica ou Peso As forças volúmicas são proporcionais à quantidade de massa e portanto à densidade. A força volúmica omnipresente sobre a Terra é o peso. O peso por unidade de massa é aceleração 
gravítica g que aponta no sentido descendente da vertical do lugar. A aceleração gravítica 
num ponto P (ver figura) é composta de aceleração gravitacional g N apontando para o centro 
de massa da Terra e de aceleração centrífuga g c apontando perpendicularmente à velocidade angular da Terra E. Ambas as forças são conservativas, isto é derivam de potenciais e exprimem‐se na forma: GM 
 




g  g N  g c ; g N   2 er   N ; g c  2E r   c
r
GM
GM GM
N  

 2  r  rsup   cte.  g 0 z  Potencial Gravitacional 


r
rsup
rsup 
 
z
g0
cte
 c   2E
r2
2
 Potencial Centrífugo 
6.16
onde G=Constante gravitacional universal= 6.67300 × 10‐11 m3 kg‐1 s‐2, M=Massa da Terra=5.9742 × 1024 kg, rsup=raio da Terra=~6371km, correspondente ao nível médio do mar (NMM), z=r‐rsup=cota (altitude) em relação a NMM. A aceleração centrífuga tem a mesma direção e sentido do 
raio de giração r que é o vetor que une o eixo de rotação 
com o ponto P. À superfície terrestre, g N tem módulo aproximado de go=9.81 ms‐2 sendo a aceleração centrífuga cerca de 1/300 da aceleração gravitacional. Na maioria das aplicações é suficiente considerar 


g   go ez    go z  ez ou seja ignora‐se a aceleração centrífuga. 

A força resultante do peso Fg e o seu momento de força (torque, binário) H g em relação à origem do referencial vêm dados por: 


Fg     g 0 ez dv   g 0 ez M ; M    dv  Massa




r  dv 







    g 0 ez M   rcm  Fg
H g    r     g 0 ez   dv   


M

 


Fg

rcm

6.17
Onde rcm é o vetor do centro de massa. Desse modo o momento de força do peso é o mesmo que se todo o peso fosse aplicado no centro de gravidade (centro de forças do peso ou baricentro), que é, na assumpção de gravidade constante, coincidente com o centro de massa. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 13 Forças volúmicas electromagnéticas Se o fluido estiver electricamente carregado, ficará sujeito a forças electromagnéticas na 

presença de um campo elétrico E e de uma indução magnética B . Nessas condições a dinâmica do fluido é gerida pelas leis da mecânica, termodinâmica e electromagnetismo e que é estudada pela magneto‐hidrodinâmica, aplicável em particular em plasmas ionizados e na ionosfera. A força de Coulomb num meio contínuo electricamente carregado é localmente proporcional à carga q por unidade de volume:
Dq
dv   q dv onde q é a densidade volúmica de carga. Dv
Assim a resultante da força eléctrica ou de Coulomb produzida por um campo eléctrico vem:. 

Fq   q Edv

6.18
A resultante da força magnética ou força de Lorentz, aplicada a fluidos obtem‐se como: 
 
Fm    q v  B dv



6.19
No caso de o fluido ser electricamente neutro (q=0), as forças eléctrica e magnética são nulas em qualquer ponto. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 14 6.4 Forças de superfície As forças de superfície actuam na superfície fronteira  do volume de controle . A superfície  pode ser composta de superfícies de diferentes naturezas de acordo com os seguintes critérios: a) Fixa ou móvel. Se for móvel pode ser livre (ex. superfície livre do mar), ou com movimento forçado externamente (ex. por bombeamento). b) Permeável, permitindo o fluxo de massa total ou parcial ou impermeável, isto é fechada. c) Separando meios homogéneos ou distintos (líquidos imiscíveis, gás‐sólido, gás‐líquido, líquido‐gás) Alguns dos tipos de superfícies estão ilustradas na figura que mostra um recipiente com líquido, limitado por uma parede fixa permeável ao líquido (1), sem qualquer suporte material, por uma parede rígida, imóvel e impermeável no fundo com a qual o líquido sofre atrito (2), por uma parede móvel rígida com movimento forçado (3) e pela superfície livre que separa o líquido do gás sobrejacente (4). Sobre cada uma das superfícies ou paredes são aplicadas ao fluido forças de superfície: 





Fsup    d     1d     2 d   ..  Fsup1  Fsup 2  ..

1
 2


 




Fsup1
Fsup 2
Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6.20 15 Pela 3ª Lei de Newton (lei da acção‐reacção), o fluido aplica uma força oposta sobre o meio do outro lado da superfície. Algumas das forças de superfície cancelam‐se mutuamente. A reacção da superfície da base cancela o peso. Outras são forças de atrito ou arrasto sobre as paredes sólidas (caso da sup. 2) ou aplicadas por superfícies sólidas móveis (caso da sup. 3). Representação das forças de superfície Consideremos um elemento de área d, centrado no ponto A, apoiado sobre o meio contínuo 
fluido. Essa área d tem o versor normal exterior next (apontando para fora do volume de controle). Sobre o fluido, é aplicada uma força infinitesimal: 

dFsup   d ;



    A, next 
6.21 
onde  é o vetor tensão (força por unidade de superfície em unidades N/m2=Pa (pascal) ). A tensão varia de forma contínua (a menos de uma pequena descontinuidade nas superfícies entre meios heterogéneos devido à tensão superficial). A tensão é assim função do ponto A e da orientação e sentido da normal. A tensão no ponto A decompõe‐se em tensão normal n, segundo a normal e tensão de corte ou cisalhamento , tangente à superfície: 



 




   n    ;  n    next  next ;       n
6.22 Tensor das tensões Vamos exprimir a forma como a tensão depende do versor normal. Iremos verificar que a tensão se obtem a partir de um tensor ˆ denominado tensor das tensões ou de Cauchy que depende apenas do ponto de aplicação A ou seja: 



    A, n   n  ˆ  A 
Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6.23
16 Para tal vamos calcular a aceleração de uma porção de fluido infinitesimal, centrada em A, em forma de tetraedro com arestas dispostas ao longo dos eixos x1,x2,x3. O tetraedro é uma pirâmide triangular; tem 4 faces, 3 são orientadas segundo os planos coordenados (planos perpendiculares aos eixos x1,x2,x3), de áreas d1, d2, d3. A quarta face é oblíqua com d e 
n
normal expandida em componentes na forma: 



n  n1e1  n2 e2  n3 e3 ; ni  cos  i  cosseno director na direcção i
6.24 Têm‐se que as áreas laterais vêm: d  i  ni d  (i  1, 2, 3) . Admitindo que a força resultante é apenas a resultante das forças de superfície tem‐se que a aceleração do fluido no interior do tetraedro vem dada pela 2ª lei de Newton na forma:

 

Dv
 
 
 
  n  d     e1  d 1    e2  d  2    e3  d  3   
dv



Dt


n1d 
n2 d 
n3 d  
6.25
Onde dv=(dh d)/3 é o volume infinitesimal do tetraedro de altura dh (distância da origem à face d). O volume infinitesimal dv tende mais rapidamente para zero que a área infinitesimal d. Sendo a densidade  e aceleração necessariamente finitas, tem de a resultante das forças de tensão ser nula. Tal é equivalente a escrever: 3
 
 
 
  n    ni  ei   ni  ei 
i 1
, 6.26
O que se verifica apenas se o vector da tensão se escrever na forma de produto interno da normal por um tensor (tensor das tensões): 
 




 
    n   n  ˆ   nk ek    ij ei e j   ni ij e j  ni  ei 
6.27
 
Deste modo, obtem‐se a seguinte interpretação. A tensão   ei  , é a tensão aplicada à face de 

normal ei e tem componentes  ij (j=1,2,3), segundo cada um dos eixos e j . Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 17 Define‐se tensor das pressões como o simétrico do tensor das tensões: ˆ   Pˆ
6.28 A força aplicada vem assim: 
 



    next   next  ˆ  next  Pˆ  nint  Pˆ
6.29 A resultante das forças de superfície sobre a superfície fechada  que envolve o volume de controle  pode ser dada como: 



ˆ 
Fsup    d    next  ˆd    nint  Pd



    ˆ dv      Pˆ dv


6.30
onde se aplicou o teorema de Gauss para explicitar a força resultante como o integral de volume da divergência do tensor das tensões. Em termos de componentes a força de pressão por unidade de volume vem:  P
P    P
P    P
P
P  
P
P
  Pˆ    11  21  31  e1   12  22  32  e2   13  23  33  e3
x3 
x2
x3 
 x2
x3 
 x1 x2
 x1
 x1
6.31 Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 18 Simetria do tensor das tensões Tem‐se o seguinte teorema: A aceleração angular de um elemento de fluido só pode ser finita se o tensor das tensões for simétrico. Como tal a parte anti‐simétrica de ˆ e P̂ é nula. Demonstração: Consideremos um paralelepípedo de fluido, de secção quadrada de lado dl, comprimento h alinhando segundo z rodando em torno do ponto A segundo o eixo z como na figura. O ponto de aplicação de cada tensão é o ponto médio das arestas. Deste modo aplicando a equação de balanço do momento angular do paralelepípedo rodando em torno de z tem‐se: 2
Dz
dl 
2 2dl 
2  yx   xy  dl h    h dl 
2 
12  
Dt




Momento das Forças
desuperfície
Momentode Inércia do
Paralelípipedo
Aceleração
Angular
6.32
Deste modo, se dl tender para zero, haverá uma aceleração angular infinita no caso de xyyx. Deste modo, como tal não é possível, tem o momento ser nulo e portanto xy=yx. Generalizando a qualquer par de direcções, conclui‐se que os tensores das tensões e das pressões são simétricos. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 19 Decomposição do tensor das tensões O tensor das tensões é simétrico, tendo 3 tensões normais e 3 de corte:  xx  xy  xz   xx  xy  xz 

 

ˆ   yx  yy  yz    xy  yy  yz  ;
       
 zx zy zz   xz yz zz 
 xx , yy , zz : tensões normais;
 xy   yx , xz   zx , yz   zy : tensões de corte;
6.33
O tensor decompõe‐se em parte isotrópica e anisotrópica (de traço nulo):  ˆ
 

ˆ
ˆ   Tr (ˆ)   ˆ  Tr (ˆ)   -pˆ  ˆ0
3
3




parte isotrópica= -pˆ
parte anisotópica=ˆ0
6.34
onde p=-
1
 xx   yy   zz 
3
6.35 é a pressão normal média e ˆ0 é o tensor de atrito, correspondente à parte anisotrópica de ˆ . 0
As tensões de corte de ˆ são as componentes de ˆ 0 fora da diagonal ou seja ˆij  ˆij (i  j ) . 6.5 ‐ Equação local do momento linear ou equação de Cauchy Num domínio material (R), imerso no seio de um fluido, portanto não sujeito a tensões superficiais, a taxa de variação do momento linear num referencial inercial iguala a resultante das forças volúmicas e de superfície ou seja: 



Dp
Dv


dv  Fres    f dv     ˆ dv


Dt  ( R ) Dt
6.36

onde f é força volúmica por unidade de volume. Sendo a equação anterior, válida para qualquer volume material arbitrariamente pequeno, obtém‐se a equação Lagrangeana de balanço do momento linear num referencial inercial ou equação de Cauchy: 


Dv

   ˆ   f    Pˆ   f (Equação de Cauchy) Dt
6.37
Esta equação tem a forma genérica de uma equação local de balanço de uma grandeza 
extensiva. Neste caso a densidade mássica de momento linear é a velocidade v com a Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 20 densidade de fluxo difusivo ou substancial de momento linear = Jˆv  Pˆ (tensor das pressões) 

e a taxa de geração de momento linear =  v  f (força volúmica por unidade de massa). A forma Euleriana de balanço de momento linear num referencial inercial obtem‐se expandindo a derivada Lagrangeana da velocidade e recorrendo à equação Euleriana da continuidade. 

 v

ˆ
   P   vv   f
t


6.38

onde  vv é a densidade de fluxo advectivo de momento linear resultante do transporte de momento linear pelo fluxo de massa. A demonstração baseia‐se na sequência de igualdades: 


Dv
   v
 
 v 

    v  v  
     vv   v
Dt
 t
 t
 
 




v


 t

=0, Eq. Euleriana da Continuidade
6.39
Na primeira igualdade usou‐se a definição de derivada Lagrangeana, na segunda derivadas de produto e na terceira a equação Euleriana da continuidade. A densidade de fluxo de momento é a quantidade de momento linear que atravessa a unidade de superfície numa unidade de tempo e tem as mesmas unidades da pressão (pascal). Num fluido em repouso a densidade de fluxo advectivo de momento linear é nula dado que a velocidade é nula. 6.6 ‐ Equações Constitutivas dos meios contínuos A expressão do tensor das tensões num meio contínuo (sólido ou fluido) permite conhecer as forças que o meio exerce nas superfícies de contacto. Estas podem ser as paredes laterais de um recipiente que o contem ou ainda a força que será exercida num corpo imerso num fluido. As tensões internas podem ser muito elevadas porque podem constituir a força de reacção ao peso ou então serem as forças responsáveis pela coesão e forma de um meio. As tensões (stress) num meio crescem em geral com a deformação (strain) em função do respectivo comportamento elástico e plástico e também crescem com a taxa de deformação (strain rate) em função do comportamento viscoso. O comportamento elástico de uma tira elástica de secção  e comprimento L traduz‐se na proporcionalidade entre a variação relativa do comprimento L/L e a tensão aplicada na secção: =força F/secção . Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 21 Para movimento a uma dimensão x, tem‐se: F
 L 
 E
  E xx ; E=módulo de elasticidade deYoung

 2L 
1

T
ˆ    Ru     Ru    tensor de deformação =

2

 partesimétrica do gradiente Lagrangeano do vector deslocamento u  xx 
6.40
Os fluidos são colocados em movimento no sentido de tensões de corte (shear stress) a ele aplicadas. Tal é devido à viscosidade. Na maioria dos fluidos, ditos Newtonianos, mantendo a tensão de corte, a deformação pode crescer devido à fluidez, mantendo todavia a mesma taxa de deformação, impondo portanto um gradiente constante de velocidades. Seja =Fa/ a tensão de corte yx produzida no fluido por aplicação de uma força de atrito Fa na direcção x sobre uma área  normal a y. Tal produz um gradiente de velocidades que satisfaz a relação: F
u
 yx  a  
 2exy onde  é a viscosidade dinâmica do fluido com ê sendo o tensor taxa y
A
de deformação. As equações constitutivas traduzem o comportamento mecânico dos meios contínuos relacionando o tensor das tensões aplicadas ˆ com o tensor deformação ˆ e o tensor taxa de deformação ê na forma: ˆ  f  ˆ, eˆ  . A dependência em ˆ e ê pode ser muito complexa nomeadamente pode ser não linear (taxas de proporcionalidade não constantes) e integrada no tempo, isto é a tensão pode depender não só dos valores instantâneos da deformação mas também dos valores num intervalo passado recente. Por exemplo certas fibras biológicas exibem relaxamento da tensão ao longo do tempo para uma deformação constante havendo portanto um comportamento histerético ou de histerese. Outro exemplo é a perda de elasticidade de um balão de pois de enchido e esvaziado várias vezes. Equações Constitutivas dos fluidos Os fluidos satisfazem a uma relação instantânea: ˆ  f  eˆ  entre o tensor de Cauchy (tensor das tensões) e o tensor taxa de deformação. Essa relação satisfaz aos postulados de Stockes: 1: ˆij é uma forma polinomial multivariada das componentes eˆpq do tensor taxa de deformação. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 22 

2: ˆij não depende explicitamente do vector posição r nem do vector velocidade v , isto é, não depende da posição nem da velocidade de translação do fluido. Tal consiste na invariância Galileana do tensor de Cauchy. Se houvesse essa dependência, o estado de tensão dependeria do referencial em que a velocidade é medida, o que não é fisicamente razoável. 3: A relação ˆ  f  eˆ  é isotrópica, isto é mantém‐se invariante para uma mudança de base de vectores em que se exprime a tensão e a taxa de deformação. 4: Se eˆij  0 ou seja se o fluido estiver em repouso, translação ou rotação sólida, então ˆij   p ij onde p é a pressão termodinâmica. Se ˆij   p ij em todas as condições, o fluido é dito perfeito ou invíscido, isto é a sua viscosidade é nula. Tendo em conta os postulados 1 e 2 pode escrever‐se a relação polinomial, usando a convenção de Einstein:  ij 
 ij
 ijkl ekl   ijklmn ekl emn  ....
 

termo
independente
termo
linear
termo quadrático
6.41
Vamos admitir a relação mais simples que inclui apenas o termo independente e o termo linear. O postulado 4 dá‐nos  ij
  p . O postulado 3 exige que o tensor de 4ª ordem  seja isotrópico o que significa que é invariante para uma transformação de base. Para tal 
consideremos o tensor  expresso na b.o.n. (base ortonormada) dos versores e j
se obtém pela matriz de transformação T a partir da b.o.n dos versores nesta base obtém‐se como:  'i ' j ' k ' l '
A 
f i . As componentes ’  ijklTi 'iT j ' jTk ' k Tl 'l . A matriz T é ortogonal ou seja a sua inversa é a transposta, o que significa que TijTkj
sse ijkl

 Tij fi que  T jiT jk   ik . O tensor  é isotrópico   'ijkl , i, j, k , l . forma mais simples de um tensor isotrópico de 4ª ordem é:  ijkl    ij kl     ik  jl   il jk  onde  ,  são constantes escalares. Na verdade, substituindo tem‐se:  'i ' j ' k ' l '
 i ' j ' k ' l '    i ' j ' k ' l '     i ' k ' j ' l '   i ' l ' j ' k '  . Dessa forma obtem‐se a relação linear mais simples entre o tensor das tensões e das taxas de deformação, válida para fluidos Newtonianos. O termo linear da relação constitutiva é então: 
 ijkl ekl   ij ekk  2  eij   ij    v   2  eij . Fluidos Newtonianos Os fluidos Newtonianos satisfazem à relação de Hooke generalizada em que a tensão depende linearmente do tensor taxa de deformação (anulam‐se os termos quadrático): 
 ij   p ij   ij    v   2  eij
Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 6.42
23 Decompondo eij em parte isotrópica e anisotrópica: eij

1

   v   ij  eij0 vem: 3

2 


 ij    p    
 eij0   p ij   ij0
   v   ij  2
3 




p

onde a pressão média vem p  p  k   v
 ij0
6.43
2
;k   
 viscosidade volúmica . O tensor 3
de atrito  ij depende apenas das taxas de deformação de corte, presentes na componente 0
anisotrópica de ê sendo o coeficiente de proporcionalidade =viscosidade dinâmica. Viscosidade volúmica k As dimensões físicas de  e k são idênticas. Ora []=[k]=pressão/(velocidade/comprimento)= =kgm‐1s‐1. Consideremos uma esfera de gás ideal com volume V, contraído ou expandido 
isotropicamente. A taxa relativa de variação do volume é   v 
1 DV
. Seja p pressão V Dt
exercida nas paredes. Por outro lado a pressão termodinâmica vale, pela equação de estado: nR *T
onde n=número de moles, T=temperatura absoluta e R*=8.314 J/(K mol) é a p
V
constante universal dos gases. Tem‐se então a viscosidade volúmica k dada por:  p  p
 1 DV 


 V Dt 
k
, 6.44
o que nos dá uma medida do acréscimo da pressão média em relação à pressão termodinâmica quando o fluido é comprimido a uma certa taxa relativa. Mostra‐se que a viscosidade volúmica k é rigorosamente nula em gases monoatómicos. Na maior parte dos casos de interesse o acréscimo de pressão p  p é desprezável ou nulo, excepto em vibrações sonoras ultrasónicas. O anulamento da viscosidade volúmica corresponde à hipótese de Stockes, que assumiremos na sequência do texto. Viscosidade dinâmica  A viscosidade dinâmica é o coeficiente de proporcionalidade entre a tensão de corte e a taxa de deformação de corte. Para o mostrar admitamos uma tensão de corte 21 segundo x1 Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 24 actuando no eixo x2 a partir do repouso. Tal pode‐se simular fazendo deslocar uma placa sólida alinhada segundo x1 no interior do fluido. A tensão provoca um campo de velocidade horizontal u1(x2). Assim tem‐se  21  2  e21  2 
D
u1
1  u1 u2 
D
onde 



Dt
x2
2  x2 x1 
Dt
é a taxa de variação do ângulo com a direcção x2 que faz uma linha material inicialmente alinhada segundo x2. A viscosidade dinâmica exprime‐se ainda na forma: = onde  é a viscosidade cinemática com dimensões unicamente cinemáticas de m2s‐1. Para o ar a PTN (25ºC e 1000 hPa  pressão e temperatura normal), (ar)=1.74x10‐5 kgm‐1s‐1. A viscosidade dos líquidos é muito superior como mostra a tabela para a temperatura de 25ºC (em kgm‐1s‐1 ): (água)= 8.94x10‐4 ; (azeite)=8.1x10‐2 ; (sangue)~ 3x10‐3 a 3x10‐4 (37ºC); (alcatrão)=2.3x108. Quanto maior a viscosidade menor a capacidade de o fluido escoar ou seja menor a fluidez. A viscosidade aumenta com a temperatura absoluta T nos gases de acordo com a fórmula de Sutherland: aT 1/2
 T  
; a, b  constantes empíricas
1 b / T
6.45
Nos líquidos, a viscosidade diminui com a temperatura absoluta de acordo com a aproximação: b / T c  
 T   a10
; a, b, c  constantes empíricas
6.46
6.7 – Equação de Navier‐Stockes Vamos estabelecer a equação local do momento linear para os fluidos Newtonianos. Divergência do tensor das tensões Retomemos a divergência do tensor das tensões interveniente na equação de Cauchy do momento linear. Nos fluidos Newtonianos com a hipótese de Stockes, a divergência do tensor das tensões escreve‐se: Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 25 
2
  ij
 

  ˆ    Pˆ  e j
 p   2    e       v    p  f at
3
xi



f at
6.47
onde o termo na pressão é a força do gradiente de pressão que aponta no sentido do maior 
decréscimo das pressões. O termo viscoso é a força de atrito f at por unidade de massa (em ms‐2). Num fluido com viscosidade constante  e após substituir eij 
1  v j vi


2  xi x j

 obtem‐se: 
 
  1
    p    2 v      v  
3

 
Para fluidos incompressíveis, ou seja em que   v  0 tem‐se: 6.48

    p   2 v 6.49 Finalmente num fluido perfeito ou invíscido (=0), tem‐se:     p 6.50 Equações de Navier‐Stockes As equações locais que governam os fluidos Newtonianos são conhecidas como equações de Navier‐Stockes em homenagem ao físico francês Claude‐Louis Navier (1785‐1836) e ao matemático inglês Sir George Gabriel Stokes (1819‐1903). Assim para um fluido Newtoniano de viscosidade dinâmica constante têm‐se as equações do momento linear e da continuidade: 

v 
1

 

 v  v   p  2v      v   f  Equação do Momento Linear 

t
3


     v   0  Equação da Continuidade 
t
6.51 onde se expandiu a derivada Lagrangeana da velocidade e se usou a viscosidade cinemática =/. A equação do momento pode re‐escrever‐se graças à expansão do termo advectivo na forma 

 






de Weber: v  v    v  v  2     v com     v  vorticidade . Usando ainda a 



igualdade vectorial  2 v  Lap v      v       grad  div v   rot  rot v  , obtem‐se: Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 26 
  1
 
v
 

4
   v  v  2     v  p       v        f
t

3

6.52
Esta equação mostra que as acelerações ou desacelerações locais podem ser devidas a:  
1) gradientes de energia cinética  v  v  2 
2) vorticidade  3) gradientes de pressão p 
4) forças volúmicas f 5) forças de atrito viscosas. 

Se o escoamento for irrotacional, tem‐se vorticidade nula,   0 ; se o fluido for 
incompressível, a velocidade é solenoidal e portanto   v  0 . Essas assumpções permitem simplificar bastante as equações de Navier‐Stockes. 6.8 ‐ Equação do momento linear num referencial não inercial Porquê usar referenciais não inerciais? Em várias condições é conveniente escrever a equação do momento linear num referencial não inercial. Por exemplo o movimento da atmosfera e do oceano terrestres são descritos num referencial não inercial em rotação sólida, solidária com o globo terrestre. Desse modo há que contar com acelerações aparentes associadas à rotação. Outro exemplo é o de um referencial ligado a um foguete a jacto acelerado pela emissão de gases. O fluido no interior sofre 
uma aceleração não inercial  a o em que 
a o é a aceleração do foguete medida no referencial inercial em repouso ligado ao solo. A velocidade de saída dos gases permite conhecer a aceleração do foguete. A escolha do referencial na qual se exprimem as quantidades (vector posição, velocidade e aceleração) depende do interesse particular do problema a resolver. Como regra, se o fluido é mantido dentro de um volume limitado por certas paredes sólidas (canal, turbina, canalização, motor a jacto), convirá escolher o referencial ligado a essas paredes sólidas. O volume de Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 27 controle escolhido num problema de balanço de momento linear tem então partes fixas ligadas às estruturas às quais está ligado o referencial e pode também ter peças móveis que são colocadas em movimento pelo fluido. Por exemplo o bloco de cilindros de um motor de explosão com admissão e escape de gases que fazem mover os êmbolos. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 28 Equações num referencial não inercial Acelerações aparentes Consideremos um referencial inercial no qual o vector posição de uma partícula de fluido arbitrária em 
movimento é rF (t ) . O mesmo vector pode exprimir‐se num referencial não inercial com origem em movimento 
rO  t  na qual está centrado uma base ortonormada de 
versores ei (t ) (i  1, 2, 3) , variável no tempo, por exemplo sujeita a uma rotação. O vector posição da 

partícula nessa base é, na C.E.: r  t   xi (t )ei (t ) . Assim tem‐se a relação: 




rF (t )  rO  t   r  t   rO  t   xi (t )ei (t )
6.53
onde xi (t ) (i  1, 2, 3) são as coordenadas na base móvel de versores. De modo a manter permanentemente ângulos rectos entre os versores da base, estes sofrem em cada elemento 

de tempo dt, rotações elementares de um ângulo segundo d   dt com eixo de rotação 
dado por uma velocidade angular (t ) que pode ser fixa ou variável, quer em módulo, quer em direcção. Mostra‐se que: 
dei (t )  
   ei . dt
Vamos agora calcular a velocidade da partícula de fluido no referencial inercial: 




drO Dr  D  xi (t )ei (t )    Dxi (t )
de (t )
DrF 
 vF 

 vO 
 vO  ei (t )
 xi (t ) i
DtF
dt Dt F
Dt
Dt
dt




vO
 
 
   
 vO  v  xi (t )   ei  vO  v    r


Dr
 
v  ei ( t ) vi ( t ) 
Dt
6.54

  Dxi (t ) Dr

onde vO é a velocidade da origem do referencial, v  ei (t )
é a velocidade 
Dt
Dt
 
medida no referencial (sistema de eixos) em movimento.   r é a velocidade angular aparente devida à rotação dos eixos. 
A aceleração a F da partícula no referencial não inercial é: Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 29  






D  vi (t )ei (t )  d    Dr
dvO Dv D   r
DvF 

 aF 


 aO 

r 

Dt F
dt Dt F
DtF
Dt
dt
Dt F





  
v  r
aO



 
  
  d 
dei (t )   
Dv
  Dvi (t )

 aO  ei (t )
 vi (t )
   v      r  aO 
2 v  r 
r
Dt 
dt
Dt
dt

 


 Dv
a
Dt





 v
6.55 
 Dv
onde a 
é a aceleração medida no referencial em movimento e todos os outros termos Dt
adicionais são acelerações aparentes. O sub‐indice F na derivada Lagrangeana indica que esta é calculada no referencial fixo inercial. A derivada Lagrangeana D/Dt é calculada no referencial não inercial em movimento.







No caso em que haja repouso ( v  0 ), só haverá aceleração centrípeta     r , 
d 

aceleração aO da origem do referencial e o termo da aceleração angular  r . A dt





aceleração 2   v é devida à velocidade v no referencial não inercial e à rotação; esta aceleração denomina‐se aceleração de Coriolis. A derivada Lagrangeana D/Dt, calculada no referencial não inercial admite, tal como para o referencial inercial, a decomposição em derivada local e advectiva: D  




  v  
 v1
 v2
 v3
onde as derivadas parciais são calculadas Dt t
t x1 , x2 , x3
x1
x2
x3
em relação às coordenadas cartesianas do referencial móvel. Equação do momento linear no referencial não inercial A equação Lagrangeana do momento no referencial móvel vem: 


  
  d 
Dv
DvF  


  aO  2   v      r 
r 
Dt
Dt F 
dt






ˆ   f    a  2   v      r  d   r 
P


 O

 
dt

Forças
Forças



de pressão
volúmicas






   Pˆ   f   f ap





Forças aparentes= f ap
6.56

onde a soma das acelerações aparentes é sintetizada na aceleração fap . Esta equação reduz‐se à equação de balanço num referencial inercial no caso de velocidade angular nula e 
   d 

acelerações linear e angular nulas: aO  0 ;   0;
 0 ou seja no caso em que a dt
aceleração aparente se anula. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 30 Pode mostrar‐se que a equação da continuidade não sofre alteração formal num referencial não inercial isto é, escreve‐se igualmente D
 

   v 
    v   0
t
Dt
6.57
onde as derivadas parciais são sempre calculadas em relação às coordenadas do referencial 
móvel e a velocidade v é a medida no referencial móvel. Equação de balanço de massa num volume de controle Seja (t) um volume de controle descrito num referencial em geral não inercial. A situação mais conveniente é aquela em que no volume de controle haja peças em repouso às quais o referencial (origem e eixos) estão ligados. Outro critério de escolha do referencial é aquele para o qual o escoamento seja estacionário, isto é 
 0 . t
A equação da taxa de variação da massa M no interior de  é formalmente idêntica àquela obtida para um referencial inercial: DM

 
  nint   v  vsup  d 

Dt
6.58
onde a massa apenas varia por importação na fronteira. Se a superfície limite ou partes dela 

estiverem ligadas ao referencial então, localmente vsup  0 . Em partes fechadas da superfície 
 
limite, a velocidade relativa é nula: v  vsup  0 . Equação local de balanço de momento linear Conjugando as equações da continuidade e do momento na forma Lagrangeana, obtemos a equação do momento linear na forma Euleriana: 


 v

   Pˆ   vv   f   f ap com
t


  
  d 

f ap   aO  2   v      r 
r
dt






6.59
Esta é a forma mais apropriada para usar no cálculo do balanço de momento linear num volume de controle. Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires 31 Equação de balanço de momento linear num volume de controle e referencial não inercial 
p , calculado no referencial não inercial, ao longo do volume de controle é 


p    vdv    vi (t )ei dv . Este momento linear varia conforme o O momento linear dado por: 

referencial que se considere e portanto não é obviamente o mesmo que o calculado no 
referencial não inercial em repouso. Dado que nos interessa calcular a variação de p no 
referencial em movimento, a sua taxa de variação é calculada na condição de versores ei fixos. 
p recorrendo ao teorema de Leibnitz Desta forma pode escrever‐se a taxa de variação de 

dp
 v
  
 
dv   nint  vsup v d 
 t

dt 



 Taxa
deVariaçãode momento devida
Termode variação
localdo momento
à variaçãoàs fronteiras móveis
6.60
Substituindo a derivada local pela expressão dada na equação Euleriana do momento escrevemos então a Equação de balanço de momento linear num volume de controle e referencial não inercial como: 



dp


  
  nint  Pˆ d    nint   v  vsup  v  d     fdv    f ap dv  Faplic




dt 

 
 Ou
 

 
tras Forças


Forças de Superfície
Taxa de Importação de Momento nas
fronteiras abertas
Forças Volúmicas
Forças nãoinerciais
6.61 Mecânica de Fluidos – FCUL – DEGGE – Prof. Carlos Pires Aplicadas