Livro5

Mecanismos e Dinâmica das Máquinas
Capítulo 5 Cinemática de
corpos rígidos
3.1 Movimento Linear de um ponto
Velocidade:
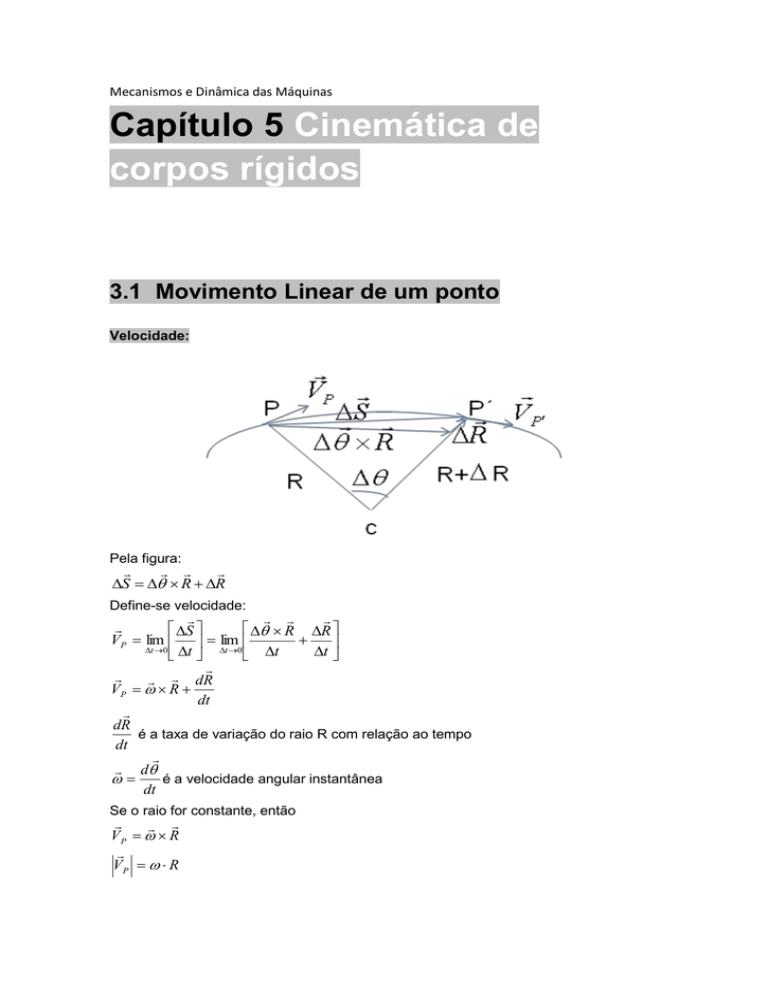
Pela figura:

 

S    R  R
Define-se velocidade:

 


 S 
   R R 
VP  lim    lim 


t 0 t
t 0
t 
 
 t


  dR
VP    R 
dt

dR
é a taxa de variação do raio R com relação ao tempo
dt

 d

é a velocidade angular instantânea
dt
Se o raio for constante, então

 
VP    R

VP    R
Direção tangente a trajetória no ponto P e com o mesmo sentido do deslocamento do
ponto P.
Aceleração:
É a taxa de variação instantânea da velocidade com o tempo.
As velocidades nos pontos P e P´ podem ser representados pelo polígono.

 n
t
V P  VP  VP
VP
sen 
Vp
n


 n
 VP n  d 
AP  lim 
 VP

t 0
 t  dt

 n  
    dR 
AP    VP      R 

dt 


 n  
    dR 
AP    VP      R 

dt 

 

 t
VP ´VP  dVP t
AP  lim 

t 0
dt
 t 

 t d    dR 
AP    R 

dt 
dt 


 t d   dR d 2 R
AP 
 R 

dt
dt dt 2

 n  t
AP  AP  AP
Se o raio for constante, então:


 n   
AP      R ,
 t d 
AP 
R,
dt
 n
AP   2  R
 t
AP    R
Observação: A direção da aceleração normal é perpendicular a trajetória e o seu
sentido é em direção ao centro de curvatura C da trajetória. A direção da aceleração
tangencial é tangente a trajetória é o de variar a velocidade.
3.2 Movimento angular
Uma partícula infinitamente pequena tem somente movimento linear. O movimento
angular é caracterizado como o movimento de uma linha de um corpo.
Na análise de máquinas, o movimento angular de uma peça é determinado pelo
movimento angular de uma reta fixa a essa peça.
3.3 Movimento relativo



VP / Q  VP  VQ



VQ / P  VQ  VP
3.4 Análise da velocidade e aceleração por
cálculo vetorial

   
VP  V0  V    R

V P é a velocidade de P em relação a XYZ

V0 é a velocidade da origem xyz em relação a XYZ

V é a velocidade de P em relação a xyz

 é a velocidade angular do sistema xyz em relação a XYZ

R é o vetor posição de P em relação a xyz





      
AP  A0  A  2  V    R      R

AP é a aceleração de P em relação a XYZ

A0 é a aceleração da origem xyz em relação a XYZ

A é a aceleração de P em relação a xyz
3.5 Determinação gráfica de velocidades em
mecanismos
Utiliza-se das equações do movimento relativo;
Cálculo com rapidez, com pouco equacionamento.



VP / Q  VP  VQ



VP  VP / Q  VQ

V P : Módulo desconhecido e direção conhecida;

VP / Q : Módulo desconhecido e direção conhecida;

VQ : Módulo e direção conhecidos.
A) Velocidade relativa em partículas de uma peça comum:

A partícula Q da figura pode ter uma velocidade absoluta VQ e o corpo com uma

velocidade de rotação  . Se a observação do movimento for em relação ao ponto Q,
então Q estará em repouso e o corpo poderá ter movimento de rotação em torno de Q.
Uma partícula do corpo, tal como P da figura, pode mover-se em trajetória

circunferencial em torno de Q. A velocidade VP / Q tem direção perpendicular a PQ e

sentido conforme  .

VP / Q    PQ


VP / Q e VQ / P possuem módulos iguais, mas sentidos opostos.
Exercícios:
1) Calcule VC onde 2  15 rad/s no sentido anti-horário.
O2 B  2,5in
BC  8in
2) Considere o mecanismo da figura. A velocidade angular da manivela
acionadora é 2  20 rad/s no sentido horário e as velocidades dos pontos D,
C e P devem ser calculadas.
O2 B  6in
BC  15in
BC  9in
B) Velocidade relativa de partículas coincidentes em peças separadas:
P3 pertence a peça 3
Q2 pertence a peça 2
Não há velocidade relativa na direção normal

V P 3 / Q 2 na direção tangencial
Neste caso há uma limitação do movimento relativo guiando o ponto P através
de uma trajetória predeterminada.
A partícula P3 não pode deslocar-se em relação a Q2 na direção normal n-n,
mas permite o movimento relativo entre esses pontos na direção t-t. portanto

V P 3 / Q 2 somente poderá estar na direção tangente à guia.
Exercícios:
Uma came de disco gira no sentido anti-horário a uma velocidade angular
constante  2  10 rad/s. Usam-se molas (não mostradas) para manter o
contato dos seguidores com a came. Para a fase mostrada, determine VA4 do
ponto A4 do seguidor oscilante e VB5 do seguidor de ponta.
C) Velocidade relativa de partículas coincidentes no ponto de contato de
elementos rodantes:

Para não haver deslizamento VP3 / P 2  0 .
Exercícios:
No mecanismo, a engrenagem 2 gira em torno de O2 com velocidade angular
constante  2  10 rad/s e a engrenagem 3 rola sobre a engrenagem 2.
Determine as imagens de velocidades das peças 2 e 3.
O2 A  50 mm
AB  100 mm
O4 B  200 mm
3.6 Determinação gráfica de acelerações em
mecanismos



AB  AA  AB / A
 

A  AN  AT
AN 
V2
 R 2
R
A T  R
A
A   A 
N 2
T 2
A) Aceleração linear:
O2 B  100 mm
BC  200 mm
2  3 rad/s
AC=?
B) Aceleração angular e imagem da aceleração:

AT C / B
BC
Exercícios:
O2 A  102 mm
AB  203 mm
AC  102 mm
CB  152 mm
2  30 rad/s
 2  240 rad/s2
AB, AC =?
C) Aceleração relativa de partículas de peças separadas, componente de
Coriolis da acelaração:
a) Deslizamento relativo entre duas peças;
b) Deve-se analisar a velocidade e aceleração de dois pontos coincidentes, cada
ponto em peças separadas.
Exercícios:
Determine AA4 do ponto A4 da peça 4 para a fase mostrada na figura, onde
2 é constante.