Cap.09 Impulso e Momentum 9.1Momentum e impulso

Cap.09 Impulso e Momentum
Do professor para o aluno ajudando na avaliação de compreensão do capítulo.
É fundamental que o aluno tenha lido o capítulo.
A colisão representa um evento durante o qual dois ou mais corpos se aproximam um do outro e
interagem por meio de forças. As forças de interação são consideradas muito maiores que
quaisquer outras forças externas presentes; portanto, podemos utilizar a aproximação do impulso.
Uma colisão pode envolver tanto contato físico, a colisão entre veículos, uma bola de bilhar
batendo nas outras e a cabeçada a uma bola (ver a foto), como
sem contato, a colisão entre partículas carregadas, o desvio de
órbita do cometa ao passar pelo Sol.
A explosão é um evento oposto ao da colisão, por exemplo,
fogos de artifício, foguete balístico.
9.1Momentum e impulso
► Uma colisão é uma interação de curta duração entre dois objetos.
► Perguntas: (a) Qual é o tempo estimado de contato entre os objetos? Exemplificar.
(b) Quais são os tempos estimados de contato entre duas bolas de bilhar e o pé do jogador com
uma bola numa cobrança de falta? Explicar por que esses tempos são tão diferentes.
(c) Você dá uma tacada com o taco numa bola de bilhar, Ela rola sobre a mesa e colide com outra
bola de bilhar. A primeira para e a segunda se move. Explicar, nesta interação, como surgiu a
força que fez a primeira bola parar. Do mesmo modo, como se explica o início de movimento
da segunda bola. Se o corpo para ou inicia o movimento, então existem forças que agem
sobre as bolinhas. Explique o surgimento das forças.
► A força pode ser constante, dependente da velocidade, do tempo e da posição. Os dois
primeiros tipos de forças foram estudados nos capítulos anteriores, Força dependente de tempo é o
objeto de estudo neste capítulo e, a dependente da posição, nos capítulos posteriores.
► Pergunta: O que é força impulsiva?
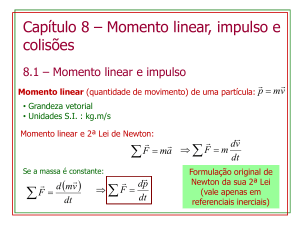
► Momento linear ou momentum (plural é momenta) de uma partícula ou um corpo de
massa m movendo-se com velocidade v é definido como produto da massa e da velocidade da
partícula:
rr
p = mv
► Note-se que o momento linear é um vetor e, como a massa é escalar de valor positivo, então o
vetor momento linear segue a mesma orientação e direção do vetor velocidade.
► Sua unidade é [p] = [ kg m/s].
► Podemos utilizar esta grandeza definida e escrever a segunda Lei de Newton na forma
rrr
r
dv d (mv ) dp
F (t ) = m
=
=
dt
dt
dt
► Esta equação mostra que a taxa de variação do momento linear de uma partícula ao longo
do tempo é igual à força resultante que age sobre a partícula.
► Nota: Esta forma da Segunda Lei de Newton é a maneira pela qual Newton apresentou a lei
e, na verdade, é mais geral que apresentada no Cap. 5. Além de situações nas quais o vetor
velocidade varia com o tempo, podemos usar a equação original para estudar fenômenos nos
quais a massa muda. Por exemplo, a massa de um foguete muda conforme o combustível é
queimado e ejetado do foguete.
► Impulso
► A componente x da equação é escrita
► O termo da esquerda expressa a variaçã o do momento linear.
► O termo da direita é uma grandeza
definida como impulso J,
► As duas expressões acima formam o enunciado importante conhecido como teorema do
impulso-momento:
A variação no momento de uma partícula é igual ao impulso da força resultante agindo sobre a
partícula,
r r
Dp = J
.
► Perguntas: (a) O impulso é um vetor? (b) Qual é a sua unidade? (c) O impulso é uma
propriedade de uma partícula, ou seja, qual é o seu significado?
► Numa colisão, entre dois corpos m1 e m2, as forças de interação
F12 e F21 são, respectivamente, de corpo 1 sobre 2 e vice-versa. As
forças F12 e F21constituem um par ação-reação, |F12|| = | F21|.
► A força aumenta durante a compressão e atinge valor máximo, Fmax, no instante em que o
corpo A (ou B) esteja em repouso, atinge o instante
de máxima compressão, e, depois, a força de
repulsão da estrutura molecular dos corpos começa a
dominar e inicia o processo de expansão, separando
os corpos. Todo este evento acontece no intervalo de
tempo Dt muito curto na ordem de ms.
► Pergunta: Se a figura do parágrafo anterior representa a variação da força de interação F12 ,
de corpo 1 sobre 2, como representaria a variação da força de interação F21, de corpo 2 sobre 1?
► Pergunta: Por que se calcula a área do retângulo e não a área
sob a curva?
► Pergunta: Qual é a vantagem de se utilizar o teorema impulsomomento?
► Estudar o texto explicativo da Fig 9.6, página 243.
► Pergunta: Uma força de grande magnitude sempre
produz um impulso muito maior sobre um corpo do que
uma força de menor magnitude? Explicar.
Resp. Não. O impulso, FDt, depende da força e do tempo
para o qual é aplicado
► Responda a questão Pare E Pense 9.1
9.2 Resolvendo problemas de impulso e momentum
► Estudar os Exemplos 9.1 e 9.2, seguindo a orientação do Box Tático 9.1.
► O que significa Aproximação de impulso?
Resp. Durante o breve intervalo de tempo de existência da força impulsiva, pode-se desprezar as
forças da gravidade sobre os corpos.
► Responda a questão Pare E Pense 9.2. E responda: há alguma semelhança com o colete à
prova de balas?
Questão: Duas partículas de massas diferentes partem do repouso. A mesma força age sobre
ambas quando elas se movem por distâncias iguais. Como os módulos de seus momentos finas se
comportam? (a) A partícula de maior massa, M, tem mais momento. (b) A partícula de menor
massa, m, tem mais momento. (c) as partículas têm momentos iguais.
Resp. (a); razão entre os momenta, (M/m)1/2.
9.3 Conservação do momentum
► A aplicação da terceira lei de Newton resulta num dos mais importantes princípios de
conservação da física. Por exemplo, considere um sistema constituído deduas partículassob aação
deforças externas, ver a figura. As forças sobre cada partículasãodescritas pelas expressões
► Nota: Depende do sistema escolhido
► Exemplo: Duas partículas(bolas)
► Sistema de uma bola: Na bola 1, as duas forças verticais se anulam, N1+ Fg1 =0, pois não há
movimento da bola nessa direção. No entanto, não há força que anula a F21 e ela é uma força
externa para 1 nesse sistema. A bola 1 não está isolada ( do mesmo modo a bola 2), p1 = F21. O
momento linear do sistema constituído de uma bola não se conserva.
►Sistema de duas bolas:As forças externas são os pares de forças verticais que se anulam, N1+
Fg1 =0 e N2+Fg2=0, pois não há movimento das bolas nessa direção. As forças de interação, a F21 e
F12 , são internas nesse sistema e formam um par de ação e reação. Quando somamos todas as
forças do sistema, as forças internas se cancelam. Não havendo nenhuma força atuando no
sistema, ou seja, sistema é isolado, o momento linear do sistema se conserva.
► Perguntas: Estudar o Exemplo 9.4 (p.251). Responder: Na pag.252, o autor expressou a
conservação do momento linear do sistema Bob + carrinho na forma
onde a v2x)B é a velocidade do Bob ainda no ar ( antes de tocar o carrinho). (a) Há uma força
externa agindo sobre o Bob. Qual é essa força e por que o momento se conserva? (b) Estando o
menino no carrinho e ele decide pular para frente do mesmo, o momento do sistema se conserva?
(c) Seguindo o item (b), a velocidade do carrinho aumenta ou diminui após o salto do Bob? (d)
Quando o Bob chega no chão, o momento linear do sistema se conserva? Obs. Todos os itens
requerem explicações.
► Responda a questão Pare E Pense 9.3.
► Problema: Resolver o problema 9.57 do livro-texto.
Resolução: (a) O momentum inicial é nulo, pois o nêutron está em repouso, pi =0. Após o
decaimento, o momentum é constituído de momenta do próton, pp, e elétron, pe, figura (A).
pf = pp + pe = -1,67x10-22 i + 2,73x10-23 i = -1,39 x 10-22 i (kg m/s).
Claramente, o momentum do sistema nêutron-próton-elétron não se conserva.
A NOTA inserida no enunciado explica a necessidade de existência de uma terceira partícula,
chamada, posteriormente, de neutrino- n, para satisfazer o princípio de conservação do
momentum, figura (B).
(b) e (c) A lei de conservação do momentum leva a seguinte expressão:
pp + pe + pn = 0,
pn = - pp - pe = 1,40 x 10-22 i (kg m/s).
O neutrino deve possuir 1,40 x 10-22 kg m/s de momentum e na mesma direção e sentido do
elétron.
► 9.4 Colisões Inelásticas
► Pergunta: O que entende por colisão perfeitamente inelástica?
► O autor afirma:
► Obs. Problema de tradução: Na segunda linha do texto copiado do livro, trocar inelásticas por
elásticas.
► Cuidado! Ainda do texto acima. Quando os objetos se ricocheteiam, nem sempre, a colisão é
elástica.
Exemplo: Numa colisão bidimensional entre corpos de massas iguais, o ângulo formado entre os
vetores velocidades após a colisão é de 90 graus, se e somente se, a colisão é elástica. Isto será
provado em cap. 10.
► Responda a questão Pare E Pense 9.4.
► 9.5 Explosões
► A explosão é um evento contrário de uma colisão perfeitamente inelástica: um corpo que se
fragmenta em vários pedaços e cada um adquire momento linear. O momento linear do sistema se
conserva na explosão, pois, as forças impulsivas, além de serem forças internas, possuem
intensidade muito elevada do que as forças externas, podendo ser ignoradas.
Exemplos: fogos de artifício, foguetes balísticos e lançamento de foguete mal sucedido.
► Responda a questão Pare E Pense 9.4.
► 9.6 Momentum em Duas Dimensões
► O momento linear é um vetor e a forma usual de se tratar o movimento num plano é reduzir
este vetor em componentes X e Y. Em se tratando que o momento linear total é conservado, assim
como os seus componentes.
rrr
p f = pi ; e como p = px iˆ + p y ˆj
resulta em
p fx = pix ;
p fy = piy
► Estudar os Exemplos 9.9 e 9.10. Neste último, note-se que o componente y de momento
linear inicial é nulo. Pergunta: Por que o momento linear total se conserva nesses dois
exemplos?
Problemas
Perguntas: (b) Qual será o estado de movimento do sistema (barco e Ann) quando Ann chegar à
outra extremidade do vagão e parar? (c) Que distância o vagão percorrerá enquanto durar o
movimento da Ann?
Resp: 13,6m; (b) Fica parado. (c) 1,36m
Conceituação: O problema trata de uma colisão perfeitamente inelástica e a conservação do
momento linear do sistema (projétil+bola de madeira) na colisão é utilizada. Aqui temos um
problema, digamos, inverso. Obter a velocidade após a colisão e depois a do projétil.
Visualizamos que, após a colisão, o sistema se torna um pêndulo cujo corpo de massa do projétil
mais a da bola de madeira oscila em torno do linha vertical fazendo um pequeno arco de raio igual
ao comprimento do fio. A velocidade calculada é a do corpo quando passa pela posição mais baixa
da trajetória curva ( do arco). Para obter esta velocidade, devemos resolver, primeiramente, o
seguinte problema de dinâmica de movimento circular. O diagrama de corpo livre ou, melhor
dizendo, diagrama das forças aplicadas ao sistema deve ser construído. No diagrama deve conter,
somente, as forças de tensão no fio e gravitacional. O sistema de coordenadas, nesse, caso, a ser
utilizado pode ser o de cartesianas, cuja origem está na outra extremidade do fio, fixa ao teto. A
segunda lei de Newton é aplicada, tendo somente o componente Y:
T - ( m proj + mbola ) g = (m proj + mbola ) vL
2
A velocidade obtida, v = 4,3m/s, é a velocidade do sistema após a colisão.
Agora , volte à equação de conservação do momento linear do sistema para calcular a velocidade
do projétil.
Resp. 90,0m/s.