Problemas Resolvidos de Física

Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 29 – LEI DE GAUSS
18. Um condutor isolado de forma indefinida está carregado com uma carga de +10 µC. Dentro do
condutor há uma cavidade que contém uma carga puntiforme q = +3,0 µC. Qual é a carga (a)
nas paredes da cavidade e (b) na superfície externa do condutor?
(Pág. 50)
Solução.
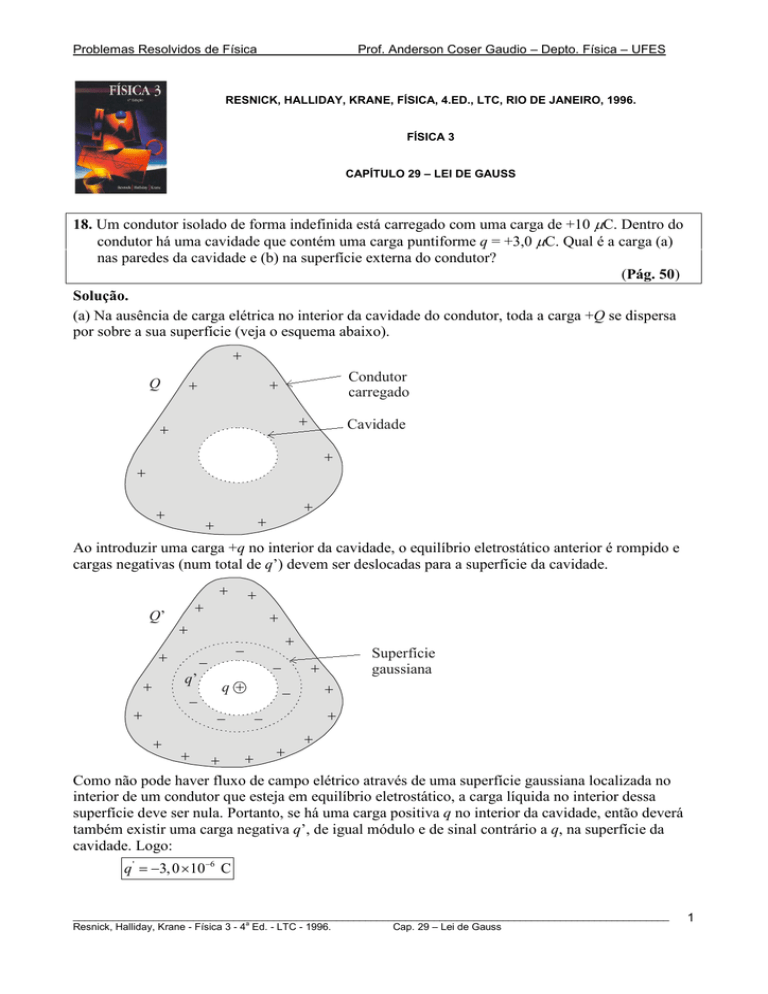
(a) Na ausência de carga elétrica no interior da cavidade do condutor, toda a carga +Q se dispersa
por sobre a sua superfície (veja o esquema abaixo).
+
Condutor
carregado
+
+
Q
+
+
Cavidade
+
+
+
+
+
+
Ao introduzir uma carga +q no interior da cavidade, o equilíbrio eletrostático anterior é rompido e
cargas negativas (num total de q’) devem ser deslocadas para a superfície da cavidade.
Q’
+
+
+
+
+
−
−
−
+
+
+
a
q’
+
+
−
q+
−
+
Superfície
gaussiana
+
+
−
+
−
+
+
+
+
Como não pode haver fluxo de campo elétrico através de uma superfície gaussiana localizada no
interior de um condutor que esteja em equilíbrio eletrostático, a carga líquida no interior dessa
superfície deve ser nula. Portanto, se há uma carga positiva q no interior da cavidade, então deverá
também existir uma carga negativa q’, de igual módulo e de sinal contrário a q, na superfície da
cavidade. Logo:
q' =
−3, 0 ×10−6 C
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 29 – Lei de Gauss
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
(b) Seja Q a carga positiva inicial no condutor. Como foi deslocada uma carga negativa q’ para a
superfície da cavidade, a carga que restará na superfície externa do condutor (Q’) será:
Q ' = Q − q ' = ( +10 µ C ) − ( −3, 0 µ C )
Q ' = +13 µ C
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 29 – Lei de Gauss
2