RESOLUÇÃO DOS EXERCÍCIOS PROPOSTOS PARA A PROVA FINAL E
SEGUNDA AVALIAÇÃO
ATENÇÃO:
(1) Alguns enunciados foram modificados devido a inconsistência dos
dados.
(2) Algumas respostas não conferem com as publicadas nas respectivas
aulas. Considerar as respostas apresentadas neste documento.
(3) Qualquer dúvida favor entrar em contato via email
(cesá[email protected]), ou pelo MSN ou pelo ORKUT.
-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x
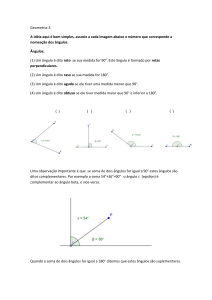
AULA 13
1 - Através do MSN, uma aluna do curso de Administração perguntou a que horas começaria a prova
de Raciocínio Lógico. Foi-lhe dada a resposta de que a prova começaria à 19 horas.
(a) Qual é o menor ângulo formado pelos ponteiros das horas e dos minutos no horário previsto
para o início da prova?
Solução: A circunferência tem 360º. Como são doze divisões
(doze horas), cada uma hora representa 360º/12 = 30º. O
ângulo será então:
5 x 30º = 150º.
(b) Qual é o triplo do complemento desse ângulo?
Resposta: O complemento de um ângulo cuja medida é “x” vale 90º - x. Esse complemento deverá
ter um valor positivo. Portanto, não existe o complemento de tal ângulo.
2 - Dois ângulos opostos pelo vértice são expressos por 3x + 22º e 5x - 40º. Qual é o suplemento
desses ângulos?
Solução: Se os dois ângulos são opostos pelo vértice então suas medidas são iguais. Assim,
3x + 22º = 5x – 40º 5x – 3x = 22º + 40º 2x = 62º x = 31º. Observe que este é o valor de x.
Devemos então calcular o valor do ângulo.
Tem-se: 3x + 22º = 3.31º + 22º = 105º.
O suplemento de um ângulo de medida é 180º - .
Portanto, o suplemento desses ângulos será 180º - 105º = 75º. Resposta: 75º.
3 - Um dos ângulos da base de um triângulo isósceles é a terça parte do ângulo do oposto à base.
Quais são as medidas dos ângulos desse triângulo?
Solução: Em um triângulo isósceles, os ângulos da base têm a mesma medida. Se “x” é a medida
do ângulo oposto à base então as medidas dos ângulos da base são x/3 e x/3. Como a soma dos
ângulos internos de qualquer triângulo é 180º, resulta: x + x/3 + x/3 = 180º 3x + x + x = 540º
5x = 540º x = 108º e x/3 = 36º. Resposta: Os ângulos medem 108º, 36º e 36º.
4 - Me desculpem as loiras. Em uma conversa com uma loira ouvi isso: a distância da minha casa
até a faculdade onde estudo é de 400m; a distância da casa de minha avó até a faculdade é de
700m e a distância da minha casa até a casa da minha avó é de 200 m. A afirmativa da loira pode
ser correta? Justifique sua resposta.
Resposta: Não. As três medidas referem-se a lados de um possível ou impossível triângulo. Como
nenhum lado pode ser maior que a soma dos outros dois, a afirmativa não é correta.
5 - Se a diferença entre dois ângulos colaterais internos é de 100º, quanto medem esses ângulos?
Solução: dois ângulos colaterais somam 180º. Se um deles é x, o outro será 180 – x.
Como a diferença é 100º, tem-se x – (180º – x) = 100º x – 180º + x = 100º 2x = 280º
x = 140º. Portanto, um dos ângulos é 140º e o outro é 180º - 140º = 40º. Resposta: 140º e 40º.
x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x
AULA 14
1 - Calcule o perímetro de um triângulo retângulo se um dos catetos mede 10 cm e a hipotenusa
mede 26 cm.
Solução: Usando o teorema de Pitágoras, determina-se o outro cateto.
a2 = b2 + c2 262 = 102 + c2 c2 = 576 c = 24.
O perímetro é a soma dos lados, portanto, o perímetro é: 10 + 26 + 24 = 60 cm.
Resposta: 60 cm
2 - As projeções dos catetos sobre a hipotenusa em um triângulo retângulo medem 6,4 cm e 3,6
cm. Calcule os catetos e a altura desse triângulo.
Solução: A solução consiste em aplicação direta das fórmulas do triângulo retângulo.
(i) a = m + n a = 6,4 + 3,6 = 10 cm
(ii) b2 = am b2 = 10.6,4 b2 = 64 b = 8 cm.
(iii) c2 = an c2 = 10.3,6 c2 = 36 c = 6 cm.
(iv) h2 = m.n h2 = 6,4.3,6 h2 = 23,04 h = 4,8 cm.
4 - A tela de monitor tem 12,75 polegadas de largura por 9,75 polegadas de altura. A medida do
monitor é dada pela medida de sua diagonal. Qual é a medida desse monitor?
Solução: a diagonal é a hipotenusa de um triângulo retângulo. Assim: a 2 = b2 + c2 a2 = 12,752 +
9,752 = 257,625 a = 16,05 16 polegadas.
5 - Um barco navega 120 km para leste e a seguir 160 km para o norte. Qual é a distância do ponto
de partida ao ponto de chegada?
Solução: Aplicação direta do teorema de Pitágoras, sendo a distância desejada igual à medida da
hipotenusa. Portanto, a2 = 1202 + 1602 = 40000 a = 200 km.
Resposta: 200 km.
6 - Um triângulo eqüilátero tem altura igual a 123 cm. Qual é seu lado?
Solução: Aplicação da fórmula da altura do triângulo eqüilátero: h = L3/2.
Tem-se: 123 = L3/2 L = 24 cm. Resposta: 24 cm.
ATENÇÃO. O enunciado original foi modificado por conter erro.
7 - Para ir à casa de sua avó, Luizinha tem que andar 400 m para o norte e a seguir 300 m para
oeste. Se fosse possível Luizinha ir direto de sua casa até a casa de sua avó?
Solução: se ela fosse direto para a casa de sua avó ela percorreria a hipotenusa de um triângulo
retângulo. Assim, a2 = 4002 + 3002 = 250000 a = 500 m. Resposta: 500 m.
8 - Um polígono tem 20 diagonais. Se seus lados são todos iguais e cada um mede 4 cm, qual é o
perímetro desse polígono?
ATENÇÃO. O enunciado original foi modificado por conter erro.
Solução: o número de diagonais de um polígono é dado por d = n.(n – 3)/2. Tem-se então:
20 = n(n – 3)/2 n(n – 3) = 40. Como n é um número inteiro, n = 8.
O polígono tem então 8 lados. O perímetro, soma de seus lados, será então: 8 x 4 = 32 cm.
Resposta: 32 cm.
Observação: a equação n(n – 3) = 40 n2 – 3n – 40 = 0 poderia ser resolvida usando a fórmula
da equação do segundo grau.
9 - Enquanto Marília descansava à sombra de uma árvore seu namorado Arthur, muito interessado
em cálculos geométricos resolveu calcular a altura da árvore. A sombra dessa árvore, às 14 horas,
media 8,4 m. Usando um bastão de 0,8 m, posicionado verticalmente, verificou que, no mesmo
instante, a sombra desse bastão media 1,2 m. Quanto Arthur deve ter encontrado para a altura da
árvore?
Solução: Por semelhança de triângulos:
Altura da árvore
altura do bastão
=
Sombra da árvore
H
8,4
=
0,8
1,2
sombra do bastão
H = 8,4.0,8/1,2 = 5,6 m.
Resposta: 5,6 m.
10 - Para determinar a altura de um prédio Luciano avaliou o ângulo de visada do topo do prédio
como sendo 60º. Afastou-se então por mais 100 m e avaliou como sendo 30º o novo ângulo de
visada do topo. Qual é então a altura desse prédio?
Solução: tan 60º = H/x e tan 30º = H/(100 + x)
Da primeira equação H = x.tan 60º e da segunda H = (100 + x).tan30º.
Igualando: x.tan 60 = (100 + x)tan 30
x.3 = (100 + x).3/3 3x = 100 + x x = 50
30º
100m
Assim: H = 50.3 = 86,6 m.
Resposta: 86,6 m
H
60º
x
11 - Quantas diagonais tem o polígono se a soma de seus ângulos internos é 720º?
Solução: a soma dos ângulos internos de um polígono é dada por S = 180.(n – 2).
Assim, 720 = 180.(n- 2) n – 2 = 4 n = 6.
O número de diagonais é então: d = n.(n – 3)/2 = 6.(6 – 3)/2 = 9.
Resposta: 9 diagonais.
12 - Calcule a medida do segmento x em cada uma das figuras:
Solução: 10/12 = 15/x
Resposta: 18 cm.
10.x = 12.15 x = 18 cm.
Solução: 100/120 = 40/x
x = 120.40/100 = 48 cm.
Resposta: 48 cm.
13 - A piscina da casa de Marina tem a forma de um quadrado cujo perímetro é 24 m. Qual é a
medida da diagonal dessa piscina?
Solução: O lado da piscina é 24/4 = 6 m.
Como d = L.2, a diagonal vale 6.2 = 8,48 m.
Resposta: 8,48 m.
14 - Calcule o raio de uma circunferência se uma corda afastada 6 cm do centro tem 16 cm de
comprimento.
Solução: R2 = 62 + 82 = 36 + 64 = 100 R = 10 cm.
Resposta: 10 cm.
8cm
6cm
15 - Se a hipotenusa de um triângulo retângulo mede 100 cm, quais serão as medidas dos catetos
desse triângulo, sabendo que um dos ângulos agudos é o dobro do outro?
Solução: A soma dos ângulos agudos do triângulo retângulo é 90º. Sejam então 2x e x estes
ângulos. Têm-se: 2x + x = 90º x = 30º e 2x = 60º.
Como o seno de um ângulo é a razão entre o cateto oposto e a hipotenusa, resulta:
(i)
cateto menor b = a.sen30º = 100.0,5 = 50 cm, e
(ii)
cateto maior c = a.sen60º = 100.0,866 = 86,6 cm.
Resposta: 50 cm e 86,6 cm.
-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-
AULA 15
1 - Calcular a área de um quadrado cuja diagonal mede 30 cm.
Solução: Como a diagonal é d = L2, L = d/2. Sendo A = L2, resulta A = (30/2)2 = 450 cm2.
Resposta: 450 cm².
2 - Calcular o comprimento da diagonal de um retângulo cujos lados são 24 cm e 10 cm.
Solução: aplicando o teorema de Pitágoras: d2 = 242 + 102 d = 26 cm.
Resposta: 26 cm.
3 - Um terreno assume a forma de um retângulo e gasta-se 28 m de tela para cercá-lo. Sabendo
que a diagonal deste retângulo é 10 m, determine a área desse terreno.
Solução: sejam b e c os lados do retângulo. Tem-se 2b + 2c = 28 ou b + c = 14 m.
Da diagonal tira-se a2 = b2 + c2 ou b2 + c2 = 100.
Resolvendo o sistema formado pela duas equações obtém-se b = 6 m e c = 8 m. A área do
retângulo é então 6.8 = 48 m².
Resposta: 48 m².
4 - No revestimento do piso de uma cozinha existem 168 lajotas retangulares de dimensões 30 cm
por 15 cm. Para fazer uma reforma nesta cozinha foi chamado um arquiteto que resolveu trocar as
lajotas retangulares por lajotas quadradas de 20 cm de lado. Quantas lajotas quadradas serão
necessárias para revestir o mesmo piso?
Solução: A área do piso é 168 x (30.15) = 75600 cm2.
Como a área de cada nova lajota é 20 x 20 = 400 cm 2, serão necessárias 75600 : 400 = 189
lajotas.
Resposta: 189.
5 - Um terreno retangular tem um dos lados o dobro do outro. O perímetro do terreno tem 78 m.
Pede – se calcular o preço desse terreno sabendo que o custo de 1m² é R$ 1200,00.
Solução: sejam x e 2x os lados do terreno. Tem-se então: 2.(x + x + 2x + 2x) = 78 ou 12x = 78
ou x = 6,5 m. Os lados são então: 6,5 m e 2.6,5 = 13 m. A área desse terreno é: 6,5 x 13 = 84,5
m2.
Ao preço de 1200,00 o m2, o preço total será 84,5 . 1200,00 = 101400,00.
Resposta: R$ 101.400,00
6 - Um losango tem área 45m² e uma de suas diagonais mede 13 m. Calcular o perímetro desse
losango.
Solução: Sejam D e d as diagonais do losango. A sua área é A = D.d/2.
Deste modo:
45 = 13.d/2 d = 45.2/13 = 90/13
O lado e a metade de cada diagonal formam um triângulo retângulo.
Assim, L2 = 6,52 + (45/13)2 = 54,232 L = 7,364 m.
O perímetro é então 4.7,364 = 29,46 m.
7 - Na casa de Marília tem uma piscina cuja forma é a indicada na
figura ao lado. Qual é a área do terreno ocupado pela piscina?
Solução: A piscina consiste de:
(i) um triângulo de base 4 m e altura 2m.
Área = 4.2/2 = 4 m2
(ii) um retângulo de base 4 m e altura 2 m.
Área = 4.2 = 8 m2.
(iii) um semicírculo de raio 2 m.
Área = (1/2).22 = 3,14.2 = 6,28 m2.
Área total = 2 + 8 + 6,28 = 16,28 m2.
Resposta: 16,28 m2
8 - A figura mostra um triângulo circunscrito a uma circunferência.
Se AD = 10 cm, DB = 12 cm, AC = 28 cm, quais são o perímetro e a área do triângulo?
Solução: pelo teorema das tangentes traçadas do mesmo ponto,
AD = AE = 10 cm
DB = FB = 12 cm
CF = CE = AC – AE = 28 – 10 = 18 cm.
Os lados são então:
AC = 28 cm;
CB = CF + FB = 18 + 12 = 30 cm;
AB = AD + DB = 10 + 12 = 22 cm
Perímetro: 28 + 30 + 22 = 80 cm.
Área: p.(p – a).(p – b).(p – c)
onde p = (a + b + c)/2 é o
semiperímetro e a, b, c são os lados.
Com p = 80/2 = 40, tem-se:
A=
40.(40 – 28).(40 – 30).(40 – 22) =
40.12.10.18
= 293,94 cm2.
Resposta: perímetro = 80 cm e área = 293,94 cm2.
-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x-x
=
F
AULA 16
1. ( CEFET - PR ) Um poliedro convexo possui duas faces triangulares, duas quadrangulares e quatro
pentagonais. Logo, a soma dos ângulos internos de todas as faces será:
(a) 3240º
(b) 3640º (c) 3840º (d) 4000º (e) 4060º
Solução: a soma dos ângulos internos de um polígono é S = 180º(n – 2) onde n é o número de
lados.
Para as faces triangulares: 2 x 180º(3 – 2) = 360º
Para as faces quadrangulares: 2 x 180º(4 – 2) = 720º
Para as faces pentagonais: 4 x 180º(5 – 2) = 2160º
Total: 360º + 720º + 2160º = 3240º. Resposta: letra (a)
2. ( CEFET - PR ) O número de vértices de um poliedro convexo de 10 faces quadrangulares é:
(a) 32 (b) 12 (c) 20 (d) 15 (e) 18
Solução: O número de arestas é a metade do número de lados. A = 10.4/2 = 20.
Fazendo F + V = A + 2, resulta: 10 + V = 20 + 2 ou V = 12. Resposta: letra (b)
3. ( PUC - SP ) Um poliedro convexo tem 3 faces pentagonais e algumas faces triangulares. Qual o
número de faces desse poliedro, sabendo-se que o número de arestas é o quádruplo do número de
faces triangulares?
(a) 4 (b) 3 (c) 5 (d) 6 (e) 8
Solução: Seja x o número de faces triangulares.
Total de arestas: 4x = (3.5 + 3.x)/2 8x = 15 + 3x 5x = 15 x = 3. Resposta: letra (b)
4. ( ITA - SP ) Um poliedro convexo tem 13 faces. De um dos seus vértices partem 6 arestas; de 6
outros vértices partem, de cada um, 4 arestas, e finalmente, de cada um dos vértices restantes
partem 3 arestas. O número de arestas desse poliedro é:
(a) 13 (b) 17 (c) 21 (d) 24 (e) 27
Solução: Seja x o número de vértices restantes.
Temos, então:
Faces: F = 13
Arestas: A = (6 + 6.4 + 3x)/2 = 15 + 3x/2 (Observe que se uma aresta liga o vértice A ao vértice B
esta aresta é a mesma que liga do vértice B ao vértice A. Por esse motivo dividiu-se por 2)
Vértices: V = 1 + 6 + x = 7 + x
Fazendo: F + V = A + 2, resulta: 13 + 7 + x = 15 + 3x/2 + 2 x = 6.
Portanto, o número de arestas é 15 + 3.6/2 = 24. Resposta: letra (d)
5. ( PUC - PR ) O número de vértices de um poliedro de 8 faces triangulares e de 4 faces
quadrangulares é igual a :
(a) 10 (b) 12 (c) 40 (d) 20 (e) 8
Solução: F = 8 + 4 = 12; A = (8.3 + 4.4)/2 = 20
F + V = A + 2 12 + V = 20 + 2 V = 10. Resposta: letra (a)
6. ( PUC - PR ) Se a soma dos ângulos das faces de um poliedro regular é 1440º, então o número de
arestas desse poliedro é:
(a) 12 (b) 8
(c)6
(d)20
(e) 4
Solução: Os poliedros têm faces triangulares ou quadrangulares ou pentagonais.
Se triangulares a soma dos ângulos de uma face seria 180º. Assim, seriam 1440:180 = 8 faces
triangulares. Nesse caso temos o octaedro.
Se quadrangulares a soma dos ângulos de uma face seria 360º. Seriam então 1440 : 360 = 4 faces
quadrangulares. Não existe tal poliedro.
Para faces pentagonais, a soma dos ângulos de uma face é 180(5 – 2) = 540. Ora, 1440 : 540 não
é um número inteiro.
Portanto, o único poliedro nestas condições é o octaedro. Onde F = 8, A = 8.3/2 = 12.
Resposta: letra (a)
7. O número de vértices de um poliedro convexo constituído por doze faces triangulares é:
(a) 4
(b) 12 (c) 10
(d) 6
(e) 8
Solução: A = 12.3/2 = 18.
F + V = A + 2 12 + V = 18 + 2 V = 8. Resposta: letra (e)
8. ( CESGRANRIO - RJ ) Um poliedro convexo é formado por 4 faces triangulares, 2 faces
quadrangulares e 1 face hexagonal. O número de vértices desse poliedro é :
(a) 6 (b) 7 (c) 8
(d) 9
(e) 10
Solução: F = 4 + 2 + 1 = 7; A = (4.3 + 2.4 + 1.6)/2 = 13.
F + V = A + 2 7 + V = 13 + 2 V = 8. Resposta: letra (c)
9. ( CESGRANRIO - RJ ) Considere o poliedro regular de faces triangulares que não possui diagonais.
A soma dos ângulos das faces desse poliedro vale, em graus:
(a)180
(b) 360
(c) 540
(d) 720
(e) 900
Solução: O único poliedro regular que não possui diagonal é o tetraedro. São 4 faces triangulares.
Assim, S = 4.180 = 720º. Resposta: letra (d)
10. ( PUC - SP ) O número de vértices de um poliedro convexo que tem 8 faces triangulares e 4
faces quadrangulares é igual a:
(a) 10
(b) 12
(c) 40
(d) 20
(e) 8.
Solução: F = 8 + 4 = 12; A = (8.3 + 4.4)/2 = 20
F + V = A + 2 12 + V = 20 + 2 V = 10. Resposta: letra (a)
11. ( PUC - CAMP ) Se um poliedro convexo possui 16 faces triangulares, o seu número de vértices
é:
(a) 24 (b) 20 (c) 16 (d) 12 (e) 10
Solução: F = 16; A = 16.3/2 = 24
F + V = A + 2 16 + V = 24 + 2 V = 10. Resposta: letra (e)
12. ( PUC - SP ) Um poliedro convexo de 33 arestas possui faces triangulares e hexagonais. Sendo
6840º a soma dos ângulos internos das faces, o número de faces triangulares e hexagonais é,
respectivamente: (a) 4 e 10 (b) 7 e 7 (c) 6 e 8
(d) 5 e 9 (e) 8 e 6
Solução: sejam x e y os nºs de faces triangulares e hexagonais, respectivamente.
Para as arestas: (x.3 + y.6)/2 = 33 3x + 6y = 66 x + 2y = 22 (1)
Para os ângulos internos: x.180º + y.180º(6 – 2) = 6840º 180ºx + 720ºy = 6840º
x + 4y = 38 (2).
Resolvendo o sistema formado pelas equações (1) e (2) resulta x = 6 e y = 8. Resposta: letra (c)