Deslocamento de neutro

O PROBLEMA DO DESLOCAMENTO DE NEUTRO EM CIRCUITOS
TRIFÁSICOS ESTRELA DESEQUILIBRADOS.
Prof. Antonio Sergio Cavalcanti de Menezes
Toda instalação trifásica predial e/ou industrial é uma ligação em estrela
tipicamente desequilibrada. Isto quer dizer que nestas instalações tem que haver um
retorno de corrente que é feito através do fio de neutro que, por sua vez, deve estar em
algum lugar aterrado, isto é, bem fixado a uma ou mais barras de cobre enterradas
convenientemente no chão, fazendo o zero de referência para os circuitos.
O problema é quando este aterramento não está bem feito. Há vários fatores que
contribuem para isso e há literatura especializada que trata exclusivamente do problema do
aterramento. Mas em linhas gerais pode-se que são: fio de aterramento subdimensionado,
resistências de contato devido ao afrouxamento dos contatos elétricos, grande resistividade
do solo, etc. Isto leva ao aparecimento de uma resistência de neutro que vamos chamar de
RN.
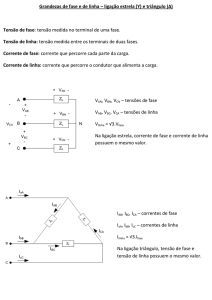
Suponha que o circuito trifásico tenha três impedâncias Z1, Z2 e Z3. Seja RN a
resistência de neutro. Seja ainda IA, IB e IC as correntes de fase de cada umas das cargas,
respectivamente, e IN a corrente de neutro. Pela Lei dos Nós, tem-se:
IN = IA + IB + IC
(1)
Substituindo cada membro da igualdade pela diferença de voltagem que é
desenvolvida em cada uma das impedâncias, e dividindo-se por elas mesmo, tem-se:
VON VAN  VON VBN  VON VCN  VON



RN
ZA
ZB
ZC
(2)
Nas considerações feitas acima, leva-se em conta que o potencial elétrico (assim
como o potencial gravitacional) de um ponto A a um ponto B é a soma de um potencial de
A para um ponto arbitrário X e de X para B. Assim, VAB = VAX + VXB e que VAB = - VBA.
IMPORTANTE!
O ponto O é o neutro do circuito e o ponto N é a referencia absoluta, isto o ponto
aonde o potencial é zero
VON é tensão do ponto O ao terra. Este ponto é o que chamamos de neutro nas
instalações prediais. Isolando algebricamente VON, tem-se:
 1
1
1
1  VAN VBN VCN
 
VON 





R
Z
Z
Z
Z
Z
ZC
A
B
C
A
B
 N
(3)
O que está entre parênteses na equação acima são as três impedâncias RN, ZA, ZB
e ZC em paralelo, isto é,
1
1
1
1
1




Z eq R N Z A Z B Z C
(4)
1
Ou, equivalentemente,
Zeq = RN//ZA//ZB//ZC
(5)
O lado direito da equação (3) é soma das correntes de fase se RN = 0, isto é, se
o circuito estiver perfeitamente aterrado. Chamaremos esta corrente de IN. Assim,
IN 
VAN VBN VCN


ZA
ZB
ZC
(6)
Assim sendo,
VON = Zeq x IN
(7)
O resultado do surgimento de uma resistência de neutro maior que zero é uma
flutuação do neutro do circuito tendo como conseqüência uma flutuação das tensões que
cada fase do circuito recebe. O resultado disso é imprevisível. As tensões do neutro e das
fases do circuito podem assumir qualquer valor no limite da tensão de linha. Na figura
abaixo, tem-se uma figura que mostra qualitativamente o que acontece nestes casos.
Fig. 1 – Diagrama fasorial de uma ligação em estrela a 3 fios.
O ponto O (neutro da instalação) se desloca imprevisivelmente do centro
geométrico do triângulo fasorial trifásico para um ponto qualquer dentro do mesmo.
Exemplo 1: (circuitos elétricos da Coleção Schaum)
Um sistema CBA trifásico, a três fios, 208V volts, tem carga ZA = 600
ZB = 6300 e ZC = 5450.. Determinar as correntes de linha, o fasor de tensão em cada
impedância e a tensão de deslocamento de neutro de neutro VON,
Solução:
Se a ligação é a tres fios, isto quer dizer que não há ligação de neutro. A
ligação de neutro está em aberto, isto é, RN =  . Se o circuito estivesse bem aterrado, a
corrente de cada linha seria:
2
IA
VAN 120  90 0


 20  90 0   j.20
0
ZA
60
IB 
VBN 12030 0

 200 0  20
0
ZB
630
VCN 120150 0
IC 

 24105 0  6,21  j23,18
0
ZC
545
A soma das três correntes acima é a corrente de neutro discutida na Eq.(6).
Assim, somando-se os três termos das equações acima, tem-se:
IN = IA + IB + IC = 13,79 + j.3,18 = 14,15 12,980
Por outro lado, a impedância equivalente total do circuito acima é dada por:
1
1
1
1



 0,167  0,167  30 0  0,2  450
0
0
Z eq 60
630
5450
= 0,167 + (0.145 – 0,084) +(0,141 –j.141) = 0,41 – j0,23 = 0,504-26,51
Zeq = (0,504-26,51)-1 = 1,98+26,510
Assim, pela equação (7), tem-se:
V0N = Zeq x IN = (1,98+26,510)x(14,15 12,980) = 28,0239,490
Na expressão acima, 28,02V é quanto vale a tensão de flutuação do neutro
do circuito (instalação).
As tensões fasorias que cada fase recebe é dada por:
VAO = VAN – VON = 120-900 – 28,0239,490
= -j120 – (21,62 + 17,82) = -21,62 –j137,82
3
= 139,21-98,910
VBO = VBN – VON = 120300 – 28,0239,490 = 92,527,140
VCO = VCN – VON = 1201500 – 28,0239,490 = 132,4161,40
Para a situação acima, tem-se o triângulo fasorial abaixo:
Fig. 2 – Diagrama fasorial para o Exemplo 1
Se no entanto, for uma ligação a quatro fios com um RN <  , o resultado é
um pouco diferente, conforme se verá abaixo:
Seja RN = 30 . Pelo exposto acima, tem-se que acrescentar RN às cargas
presentes no circuito para calcular a nova impedância Zeq :
1
1
1
1
1
+
= 0,504-26,51 + (30)-1



0
0
0
30
Z eq 60
630
645
= 0.534-250
O novo Zeq = (0.534-250 )-1 = 1,873+250
Sendo assim, a nova tensão de flutuação de neutro será:
VON = Zeq x IN = (1,873+250)x(14,15 12,980) = 26,50280
Comparado com situação anterior vê-se que a resistência de 30 de neutro
pouco altera em relação à situação em que esta resistência era infinita. No entanto se a
resistência RN cair para 5  tem-se:
VON = 20,5320
Se RN = 1  , VON = 9,632,180.
Percebe-se, então, que quanto menor a resistência de neutro, menor a
flutuação de neutro. O neutro bem aterrado “amarra” a tensão VON bem próxima do zero
4
.
Idealmente falando, se a resistência de neutro for realmente zero, a tensão do
neutro da instalação será sempre zero. Para descobrir o neutro da instalação podemos nos
valer do que os eletricistas chamam de “chave-teste”. Trata-se de uma chave de fenda
comum que tem no interior de seu cabo uma lâmpada néon. Se a lâmpada acender o ponto
é de fase; se não acender, é de neutro. Se você colocar um voltímetro AC entre este neutro e
um ponto bem aterrado, o voltímetro deve dar uma leitura de poucos volts, isto é, pouca
flutuação. No entanto, se a flutuação for grande, pode estar ocorrendo duas coisas: ou há
problemas no aterramento de neutro, ou o está ocorrendo um forte desbalanceamento, seja
na rede interna, seja na externa (de rua).
Suponha um conjunto de 3 lâmpadas incandescentes comuns. Uma de 100W,
outra de 60W e uma terceira de 40W ligadas num circuito trifásico em estrela, uma em cada
fase, supondo-se que a tensão de linha é de 380V e que a sequencia é ABC
Seja IA a corrente que circula pela carga liga à fase A (100W); seja IB a corrente que circula pela carga ligada à fase B (60W) e seja IC a corrente em C (40W). Seja
ainda RA a resistência associada à carga de 100W; RB a carga de 60W e seja RC a carga de
associada a de 40W

V2
380 / 3
RA  F 
PA
100
RB 

VF2
380 / 3

PB
60

VF2
380 / 3
RC 

PC
40
2  220 2  484
100
2  220 2  806,7
100
2  220 2  1240
40
5
IA 
VAN 22090 0

 j0,455
RA
484
IB 
VBN 220  30 0

 0,273  30 0
RB
806,7
IA 
VCN 220210 0

 0,177210 0
RC
1240
Se a resistência de neutro RN for zero, a corrente de neutro IN será a soma
das três correntes acima. Assim,
IN = IA + IA + IC = 0,245700
Se a resistência de neutro for infinita o calculo de R eq acima, e
considerando-se a equação (4) , tem-se:
1
1
1
1
1
1
1
 4,11x10-3






R eq R A R B R C 484 807 1240
 Req = 243,2 
Assim, VON = RN .IN  243,2. 0,245700 = 59,6 700
O que aconteceu neste caso foi um forte desbalanceamento do neutro
(60V!). Isto reflete nas tensões que cada carga (no caso, cada lâmpada), Para ver isso, as
contas acima são refeitas:
100W: VAO = VAN – VON = 220900 - 59,6 700  16696,60
60W: VBO = VBN – VON = 220-300 - 59,6 700  238--43,90
40W: VCO = VCN – VON = 2202100 - 59,6 700  267-1420
Na verdade, nos resultados finais os ângulos fasorias tem pouca ou nenhuma
importância prática. O que importa mesmo é saber que a lâmpada de 100W está submetida
a uma tensão de 166V, a de 60W, 238V e a de 40W, 267V. Assim sendo, as cargas estarão
sujeitas a grandes diferenças de tensão, podendo até serem queimadas.
O aconteceu neste caso foi que a situação houve um forte desbalanceamento
das tensões de cada fase do circuito, mesmo sem a resistência de neutro ser
necessariamente infinita. O diagrama abaixo ilustra o que aconteceu:
6
Supondo-se, agora, uma resistência de 30Ω de neutro e, tem-se:
1
1
1
1
1
1
1
1
1
 0,037








R eq R A R B R C R N 484 807 1240 30
Logo,
Req  26.7 o que leva a VON =
RN .IN  26.7. 0,245700
= 6,58700
A tensão que cada lâmpada está submetida é dada por:
100W: VAO = VAN – VON = 220900 - 6,58700  21490,60
60W: VBO = VBN – VON = 220-300 - 6,58700  221-320
40W: VCO = VCN – VON = 2202100 - 6,58700  2232110
Não é fácil generalizar, mas em linhas gerais pode-se dizer que as menores
cargas sofrem mais e tem mais chances de se danificarem quando há problemas na
resistência de neutro.
Se o desbalanceamento de cargas for realmente muito forte, como mostrado
abaixo, em que a lâmpada de 100W foi trocada por uma carga igualmente resistiva de
1000W (48,4 ), tem-se para a corrente de neutro com resistência de neutro zero:
IN = j.4,55 + 0,273-300 + 0,1772100 = 4,17890
Refazendo-se os calculos acima tem-se para a resistência equivalente Req:
1
1
1
1
1
1
1
1
1








R eq R A R B R C R N 48,4 807 1240 30
Req = (0,056)-1 = 17, 84 
VON = Req .IN  17,84 x 4,17890 = 74,46890
Neste caso a tensão que cada carga desta recebe é:
1000W: VAO = VAN – VON = 220900 – 74,46890  14490,50
60W: VBO = VBN – VON = 220-300 - 74,46890  265-320
40W: VCO = VCN – VON = 2202100 -74,46890  266900
No entanto, se R =  , VON  190 900. Portanto, uma desbalaceamento de
neutro de cerca de 190V! . Assim, sendo, cada carga receberia:
1000W: VAO = VAN – VON = 220900 – 190 900  31970
60W: VBO = VBN – VON = 220-300 - 190 900  353-580
40W: VCO = VCN – VON = 2202100 -190 900  357 -1230
Assim, duas das cargas estão quase no limite da tensão de linha que é 380V!
7
Exercícios propostos:
1) Resolveu-se iluminar um ambiente externo para uma festa com lâmpadas
incandescentes comuns. Como a quantidade de lâmpadas era muito grande, optou-se por
uma ligação trifásica (em estrela). Colocou-se 50 lâmpadas de 100W na fase A; 40 lâmpadas de 60W na fase B e 100 lâmpadas de 40W na fase C. Se fio de neutro desta ligação se
romper quando todas as lâmpadas estiverem acesas, que voltagens cada conjunto de
lâmpadas estará submetido? A tensão de fase é 220V.
Resp: 187,2V; 261,1V, 218,6V
2) Um certo prédio tem 60 salas comerciais. Para cada sala foram previstas 5
lâmpadas fluorescentes de 40W com reatores com 0,4 de fator de potência e um arcondicionado de 10.000 btus (1500W) com fator de potência de 0,8. Supondo-se que a tensão
de fase do prédio é 220V e instalação foi feito de maneira distribuir igualmente as salas nas
três fases e desconsiderando-se outras cargas presentes no prédio, pergunta-se:
a) Qual a corrente de neutro da instalação da instalação como um todo, se
todas as lâmpadas e arcondicionados do prédio estiverem ligados?
b) Qual tensão de neutro da instalação se medirá se 10 salas estiverem
funcionando plenamente na fase A, 20 na fase B e 17 na fase C, se, por algum motivo a
resistência de neutro for RN = 30  ? Que tensão um usuário da fase A, por exemplo, mede
na sua tomada nestas condições?
Sugestão:
Começar calculando a impedância equivalente de cada carga de cada sala, que
é a impedância das lâmpadas em paralelo com a impedância do arcondicionado.
Se Z = Z  é impedância de uma certa carga, então n impedâncias iguais a
ela em paralelo será:
Z 
Z
n

(b) Tensão de neutro da instalação: 41,23 V; o usuário irá medir na tomada
que estiver na fase aproximadamente 260 V.
8
Solução do exercício proposto 2
A potência aparente das cinco lâmpadas são:
5x 40
 500 VA; cos-1 0,4 = 66,420
0,4
A potência reativa das cinco lâmpadas são:
NL 
QL = NL x sen(66,42o) = 458,26 VAR
Para o arcondicionado, tem-se:
NA 
1500
 1875 VA ; cos-1(0,8) = 36,87O --> QA = 1125 VAR
0,8
NT =
(1500  200) 2  (458,25  1125) 2  2323,076 VA
Logo, a corrente total será:
IT =
NT
2323,08
T 
  43o  10,56  43o
V
220
ZT = 20,83 430 = 15,23 + j 14,21
Z1 = 1,04 430 = 1,523 + j 1,421
VAN 1 0 AC 220 90
VBN 2 0 AC 220 -30
VCN 3 0 AC 220 210
RA 1 5 1.523
LA 5 4 3.77M
RB 2 6 0.762
LB 6 4 1.88M
RC 3 7 0.9
LC 7 4 2.22M
RX 4 0 30
* Resistência de neutro = 30 ohms
.AC LIN 1 60HZ 60HZ
.PRINT AC VM(1,4) VM(2,4) VM(3,4) VM(4,0) IM(RX)
.END
FREQ
VM(1,4)
VM(2,4)
VM(3,4)
VM(4,0)
6.000E+01 2.597E+02 1.920E+02 2.145E+02 4.123E+01
9
IM(RX)
1.374