Leis de Kirchhoff

Capı́tulo 6
Leis de Kirchhoff
6.1
Definições
1. dois nós: B e F
2. três ramos: BAEF, BDF e BCGF
Em alguns casos, um circuito não pode ser resolvido
através de associações em série e paralelo. Nessas
3. três malhas: ABDFEA, BCGFDB e ABCGFEA
situações geralmente são necessárias outras leis, além
da lei de Ohm, para sua resolução. Estas leis adicionais são as leis de Kirchhoff, as quais propiciam uma 6.2 Primeira Lei de Kirchhoff
maneira geral e sistemática de análise de circuitos. Elas
são duas, a saber:
Uma boa introdução à Primeira Lei de Kirchhoff já foi
vista no circuito paralelo. Num dado nó entrava a cor• Primeira lei de Kirchhoff ou lei das Correntes
rente total do circuito e do mesmo nó partiam as correntes parciais para cada resistor. Como no nó não há possi• Segunda lei de Kirchhoff ou lei das Tensões
bilidade de armazenamento de cargas ou vazamento das
Para o uso destas leis são necessárias algumas mesmas, tem-se que a quantidade de cargas que chegam
ao nó é exatamente igual à quantidade de cargas que
definições:
saem do nó.
Desta constatação surge o enunciado da primeira lei
• Nó: é um ponto do circuito onde se conectam no
mı́nimo três elementos. É um ponto onde várias de Kirchhoff:
correntes se juntam ou se dividem.
“A SOMA ALG ÉBRICA DAS CORRENTES EM UM N Ó
• Ramo ou braço: é um trecho de um circuito comÉ SEMPRE IGUAL A ZERO .”
preendido entre dois nós consecutivos. Todos os
elementos pertencentes ao ramo são percorridos
pela mesma corrente elétrica.
n
∑ Ii = 0
• Malha: é um trecho de circuito que forma uma
trajetória eletricamente fechada.
(6.1)
i=0
Por convenção, consideram-se as correntes que entram em um nó como positivas e as que saem como negativas.
Considere o circuito da figura 6.2.
Ao se aplicar a lei de Kirchhoff das correntes aos nós
B e F, obtém-se:
Nó B: I1 + I2 − I3 = 0
Nó F: −I1 − I2 + I3 = 0
Figura 6.1: Circuito elétrico com dois nós
Na figura 6.1, por exemplo, identifica-se:
Observa-se que as equações dos nós B e F são na realidade as mesmas, ou seja, a aplicação da lei das correntes de Kirchhoff ao nó F não aumenta a informação
sobre o circuito. Assim, o número de equações independentes que se pode obter com a aplicação da lei das
correntes de Kirchhoff em um circuito elétrico é igual
ao número de nós menos um.
Se equação do nó B, isolarmos de um lado da igualdade as correntes que chegam no nó (nesse caso I1 e I2 ) e
57
C AP ÍTULO 6. L EIS DE K IRCHHOFF
um potencial mais elevado. Nas quedas de tensão as cargas se dirigem para um potencial mais baixo havendo o
consumo da energia das cargas convertendo-a para uma
forma de energia não-elétrica, por exemplo, calor, luz
etc. Assim, ao percorrer uma malha fechada, percebese que toda a energia entregue às cargas num trecho do
circuito elétrico é dissipada num outro trecho.
A tensão, por definição, está associada à energia cedida às cargas ou retirada das mesmas durante o seu movimento. Daı́ é obtido o enunciado da Segunda Lei de
Kirchhoff:
“A SOMA ALG ÉBRICA DAS TENS ÕES (f.e.m.s e
quedas de tensão) AO LONGO DE UMA MALHA
EL ÉTRICA É IGUAL A ZERO .”
Figura 6.2:
n
do outro lado as correntes que saem do mesmo nó (nesse
(6.2)
∑ Vi = 0
caso apenas a I3 ), temos:
i=0
I1 + I2 = I3
Para a aplicação da lei de Kirchhoff das tensões, fazObservando o resultado da equação podemos concluir
que a soma das correntes que entram no nó é igual a se necessário adotar alguns procedimentos que são dessoma das correntes que saem dele. Essa é uma outra critos a seguir:
forma de se interpretar a primeira lei de Kirchhoff.
1. Atribuir sentidos arbitrários para as correntes em
todos os ramos;
6.3
Segunda Lei de Kirchhoff
A lei de Kirchhoff das tensões é aplicada nas malhas.
Ela já foi usada no estudo dos circuitos de resistores em
série, onde a soma das quedas de tensão nos resistores é
igual à f.e.m. da fonte.
Se no circuito existe mais de uma fonte de f.e.m.
deve-se determinar a resultante das mesmas, ou seja,
somá-las considerando os seus sentidos relativos.
2. Polarizar as fontes de f.e.m. com positivo sempre
na placa maior da fonte, conforme a figura 6.4;
Figura 6.4:
3. Polarizar as quedas de tensão nos resistores usando
a convenção de elemento passivo e sentido convencional de corrente elétrica. Isto equivale a colocar a
polaridade positiva da queda de tensão no resistor
no terminal por onde a corrente entra no mesmo,
conforme a figura 6.5;
Figura 6.3:
Et = VAB +VBC +VCD
Figura 6.5:
Como a tensão em um resistor pode ser calculada
pela lei de Ohm, temos:
4. Montar a equação percorrendo a malha e somando
algebricamente as tensões. O sinal da tensão corresponde ao sinal da polaridade pela qual se ingressa no componente, independentemente do sentido da corrente elétrica.
E1 − E2 = R1 · I + R2 · I + R3 · I
+E2 − E1 + R1 · I + R2 · I + R3 · I = 0
Entenda-se que, na fonte de f.e.m., uma forma de
energia não-elétrica é convertida para elétrica cedendo
energia para as cargas, ou seja, colocando as cargas em
RODRIGO S OUZA E A LVACIR TAVARES
De acordo com o circuito apresentado na figura 6.6,
ao se aplicar a lei das tensões de Kirchhoff às malhas
ABDFEA e BCGFDB, no sentido horário, obtém-se:
58
C URSO DE E LETROMEC ÂNICA /IFSUL
C AP ÍTULO 6. L EIS DE K IRCHHOFF
3. Polarizar as fontes de tensão;
Malha ABDFEA: R1 · I1 + E2 − R2 · I2 + R4 · I1 + E1 = 0
Malha BCGFDB: −E1 + R3 · I3 + E4 + R2 · I2 − E2 = 0
4. Polarizar as quedas de tensão nos resistores de
acordo com o sentido adotado para a corrente;
5. Havendo nós, aplicar a 1a Lei de Kirchhoff,
obtendo-se Ne1 equações (Ne1 = n − 1);
6. Se o número de equações ainda não for suficiente
para resolver o circuito, aplicar a 2a Lei de Kirchhoff, onde o número de equações é dado por
Ne2 = (r − n + 1);
7. Escolher um ponto de partida e adotar um sentido
de percurso para analisar a(s) malha(s).
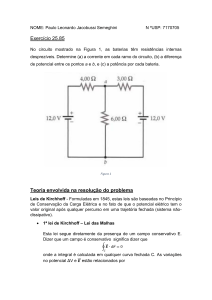
Exemplo 6.1 : Calcule o sentido e o módulo da corrente
elétrica no circuito da figura 6.7.
Figura 6.6:
No circuito da figura 6.6, existe ainda mais uma malha (a malha externa ABCGFEA). Nesta malha poderia
ser aplicada também a lei das tensões de Kirchhoff. Entretanto, como no caso da lei das correntes, a equação resultante seria dependente das duas já obtidas. Portanto,
esta equação seria inútil.
Figura 6.7:
Supondo-se que, no circuito da figura 6.6, fossem
conhecidos os valores de todas as f.e.m.s das fonResolução:
tes de tensão e todas as resistências, restariam como
1. Escolhe-se um sentido para a corrente elétrica no
incógnitas as três correntes. Para resolver um siscircuito. Por exemplo, o sentido indicado na figura
tema de equações lineares com três incógnitas são ne10.5.
cessárias três equações. Uma equação já foi obtida com
a aplicação da lei da correntes de Kirchhoff. Portanto,
2. Polarizam-se as quedas de tensão nos resistores
são necessárias mais duas, que podem ser obtidas pela
(polaridade positiva no terminal por onde a coraplicação da lei das tensões de Kirchhoff.
rente entra) e as f.e.m.s das fontes (o terminal
Em sı́ntese, pode-se concluir que, em um circuito
maior é o positivo).
elétrico com r ramos e n nós, tem-se r correntes, uma
em cada ramo. A lei das correntes de Kirchhoff fornece
3. Percorre-se a malha, somando algebricamente as
Ne1 = n − 1 equações e, portanto, a lei das tensões de
tensões (o sinal da tensão corresponde ao sinal
Kirchhoff deve fornecer Ne2 = r − n + 1 equações para
da polaridade da tensão encontrada na entrada do
que o problema possa ser resolvido.
componente).
Por exemplo, no circuito da figura 6.6, tem-se r = 3,
Estas etapas estão mostradas na figura 6.8 e na
n = 2. Se r = 3, o número de correntes é 3. O número
de equações fornecidas pela lei das correntes é Ne1 = equação abaixo.
2 − 1 = 1 e o número de equações fornecidas pela lei
das tensões é Ne2 = 3 − 1 = 2, conforme discutido anteriormente.
A seguir, apresenta-se um resumo para aplicação da
LKC e LKT.
Resumo para aplicação das Leis de Kirchhoff
Figura 6.8:
1. Identificar os nós, ramos e malhas do circuito
elétrico;
1I + 4, 7I + 3, 3I + 15 − 6 = 0
9I = −9
I = −1A
2. Atribuir para cada ramo do circuito um sentido
para a corrente elétrica;
RODRIGO S OUZA E A LVACIR TAVARES
59
C URSO DE E LETROMEC ÂNICA /IFSUL
C AP ÍTULO 6. L EIS DE K IRCHHOFF
O sinal negativo que aparece para o valor da corrente I
significa que o sentido escolhido para ela está invertido.
Neste exemplo, o sentido correto da corrente elétrica I é
para baixo na figura 6.8 e não para cima como foi arbitrado no inı́cio da resolução.
das correntes. Então, simplificando-se as equações
e colocando-as na forma de um sistema, obtém-se:

+I2
−I3 = 0
 I1
4I1
= 24

−4I1 +6I2
=0
Exemplo 6.2 : No circuito da figura 6.9, calcule os valores das correntes I1 , I2 e I3 a partir dos valores das f.e.m.s
e das resistências elétricas usando as leis de Kirchhoff.
6. Existem vários métodos para se resolver um sistema de equações. Nesse caso foi usado o método
da substituição:
Da segunda equação obtém-se:
24
= 6A
I1 =
4
Substituindo-se o valor de I1 na terceira equação
obtém-se:
−4 · 6 + 6I2 = 0; Logo:
24
I2 =
= 4A
6
Então, substituindo-se os valores de I1 e I2 na primeira equação obtém-se:
Figura 6.9:
6 + 4 − I3 = 0; Logo:
Resolução:
I3 = 10A
1. O circuito possui 2 nós, 3 ramos e 3 malhas.
6.4
2. Os sentidos de corrente e polaridades foram arbitrados conforme 6.10.
Técnica da Análise de Malhas
Partindo das Leis de Kirchhoff, várias técnicas foram
desenvolvidas com o objetivo de facilitar a resolução
de circuitos elétricos. Uma das mais conhecidas é a
Técnica de Análise de Malhas que será estudada nesta
seção.
Consideremos então o circuito da figura 6.11, em que
foi atribuı́da uma corrente em cada ramo.
Figura 6.10:
3. Aplicando-se a lei de Kirchhoff das correntes temse apenas uma equação obtida em relação aos nós,
pois nos dois nós a equação será a mesma:
Figura 6.11: Circuito para análise de malhas
I1 + I2 − I3 = 0
Pela aplicação da Lei de Kirchhoff das correntes
4. Aplicando-se a lei de Kirchhoff das tensões, tem-se temos:
duas equações obtidas pelas malhas:
I1 − I2 − I3 = 0
Malha ACDA: Começando pelo nó A, percorrendo
a malha no sentido horário e chegando novamente
ao no A tem-se:
Isolando-se I3:
+4I1 + 12 − 36 = 0
I3 = I1 − I2
Malha ABCA: Começando pelo nó A, percorrendo
a malha no sentido horário e chegando novamente
ao no A tem-se:
Logo, podemos indicar as correntes no circuito
desprezando a existência de I3 , pois esta pode ser
escrita como I1 − I2 . Então as correntes no circuito
+3, 3I2 + 2, 7I2 − 4I1 = 0
ficam como na figura 6.12.
5. Fica-se então com três equações e três incógnitas,
Consideremos agora, o mesmo circuito com uma lio que nos permite encontrar o valor de cada uma geira modificação, utilizaremos correntes de malha.
RODRIGO S OUZA E A LVACIR TAVARES
60
C URSO DE E LETROMEC ÂNICA /IFSUL
C AP ÍTULO 6. L EIS DE K IRCHHOFF
Figura 6.12: Circuito sem a corrente I3
O método da soma é um dos mais simples para se
resolver sistemas com duas equações, porém só é
possı́vel sua utilização quando as equações são dispostas de forma que, ao subtrair ou somar os polinômios
das equações, todas as incógnitas, exceto uma, se
anulam.
Muitas vezes é necessário multiplicar uma das
equações por algum valor de modo que essa situação
ocorra. Esse é o caso do sistema de equações deste
exemplo. Então devemos multiplicar a segunda equação
por 3, ficando com:
9IA
−3IB = 42
−9IA +21IB = 30
Definimos correntes de malha como a corrente que
flui apenas no perı́metro de uma malha. A corrente de
malha é indicada por uma seta curva que quase fecha em
si mesma sem cortar nenhum ramo.
Por conveniência, as correntes de malha são coloEntão, somando-se as duas equações do sistema,
cadas sempre no sentido horário e, a lei de Kirchhoff
das tensões, também é aplicada nesse mesmo sentido. tem-se:
Utilizando-se essa técnica, não é necessário a aplicação
da lei de Kirchhoff das correntes, o que simplifica a 18IB = 74
resolução do circuito.
Portanto, as correntes de malha são indicadas no cir- Logo: IB = 4A
cuito analisado conforme a figura 6.13.
Substituindo-se o valor de IB na primeira equação
temos:
9IA − 3(4) = 42
Então: IA = 6A
Figura 6.13: Circuito com correntes de malha
A corrente de malha IA corresponde à corrente I1
do circuito da figura 6.11. Enquanto a corrente IB
corresponde à corrente I2 . Porém para obtermos a
corrente I3 (que passa no ramos central) é necessário
subtrair as duas correntes, ou seja:
Conforme foi comentado anteriormente, para resolver
o circuito e encontrar o valor das correntes, basta aplicar
a lei de Kircchoff das tensões às malhas da figura 6.13. I3 = IA − IB = 6 − 4 = 2A
Como no ramos central passam duas correntes de
malha, o valor real da corrente que circula nesse ramo Como o valor de IA é maior do que IB , então o
é a diferença entre as correntes de malha. Então as sentido correto da corrente I3 é o próprio sentido de IA .
equações das malhas fica assim:
Malha A: −42 + 6IA + 3(IA − IB ) = 0
6.5
1. Determine os valores das correntes desconhecidas
no circuito da figura 6.14.
Simplificando-se a equação resulta em:
9IA − 3IB = 42
2. Determine os valores das tensões desconhecidas no
circuito da figura 6.15
Malha B: −10 + 3(IB − IA ) + 4IB = 0
3. Calcule o valor da corrente I no circuito da figura 6.16
Após simplificação fica-se com:
−3IA + 7IB = 10
4. Calcule o valor da resistência do resistor R3 no circuito da figura 6.17.
Então, para encontrar o valor das correntes, devese resolver o seguinte sistema de equações:
9IA −3IB = 42
−3IA +7IB = 10
RODRIGO S OUZA E A LVACIR TAVARES
Execı́cios
5. Sabendo que a corrente através do resistor R3 no
circuito da figura 6.18 vale 4A, calcule os valores e
os sentidos corretos das outras correntes e o valor
do resistor R3 .
61
C URSO DE E LETROMEC ÂNICA /IFSUL
C AP ÍTULO 6. L EIS DE K IRCHHOFF
Figura 6.14:
Figura 6.18:
6. Calcule os valores das correntes I2 e I3 e do resistor R2 , no circuito da figura 6.19, sabendo que a
intensidade da corrente I1 vale 0, 2A.
Figura 6.19:
Figura 6.15:
7. Calcule o valor e o sentido correto das correntes
nos ramos no circuito da figura 6.20.
Figura 6.16:
Figura 6.20:
8. Calcule os valores das correntes I1 e I2 no circuito
da figura 6.21.
9. No circuito da figura 6.22, calcule o valor da corrente I.
10. No circuito da figura 6.23, calcule os valores da
tensão VS e da resistência R.
11. Determine a potência dissipada em R1 e R2 do circuito da figura 6.24.
Figura 6.17:
RODRIGO S OUZA E A LVACIR TAVARES
62
C URSO DE E LETROMEC ÂNICA /IFSUL
C AP ÍTULO 6. L EIS DE K IRCHHOFF
12. Qual deve ser o valor do resistor R para que a corrente no ramo AB da figura 6.25 seja nula?
Figura 6.21:
Figura 6.25:
Respostas dos exercı́cios numéricos
1. I1 = 1A; I2 = 18A; I3 = 9A
2. V1 = 11V ; V2 = 2V ; V3 = −1V
Figura 6.22:
3. I = 0, 3A
4. R3 = 1Ω
5. I1 = 4A; I2 = 0; R3 = 1, 5Ω
6. I2 = 0, 8A; I3 = 0, 6A; R2 = 2, 5Ω
7. I1 = 6A; I2 = 4A; I3 = 10A
8. I1 = 9A; I2 = 1, 5A
9. I = 3A para cima
10. Vs = 14V ; R = 4Ω
11. P1 = 20mW ; P2 = 22, 5mW
Figura 6.23:
12. R = 26kΩ
Figura 6.24:
RODRIGO S OUZA E A LVACIR TAVARES
63
C URSO DE E LETROMEC ÂNICA /IFSUL