Exercício 25.85 Teoria envolvida na resolução do - IFSC-USP

NOME: Paulo Leonardo Jacobussi Semeghini
N ºUSP: 7170705
Exercício 25.85
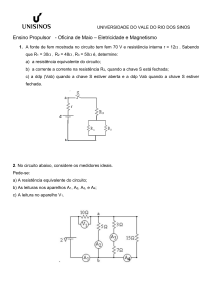
No circuito mostrado na Figura 1, as baterias têm resistências internas
desprezíveis. Determine (a) a corrente em cada ramo do circuito, (b) a diferença
de potencial entre os pontos a e b, e (c) a potência por cada bateria.
Figura 1
Teoria envolvida na resolução do problema
Leis de Kirchhoff - Formuladas em 1845, estas leis são baseadas no Princípio
de Conservação da Carga Elétrica e no fato de que o potencial elétrico tem o
valor original após qualquer percurso em uma trajetória fechada (sistema nãodissipativo).

1ª lei de Kirchhoff – Lei das Malhas
Esta lei segue diretamente da presença de um campo conservativo E.
Dizer que um campo é conservativo significa dizer que
⃗ ∙ 𝑑𝒓
⃗ =0
∮𝑬
𝐶
onde a integral é calculada em qualquer curva fechada C. As variações
⃗ estão relacionados por
no potencial ΔV e 𝑬
𝑏
⃗ ∙ 𝑑𝒓
⃗
∆𝑉 = 𝑉𝑎 − 𝑉𝑏 = − ∮ 𝑬
𝑎
o que significa que a soma das variações no potencial em qualquer
trajetória fechada é igual a zero.

2ª lei de Kirchhoff - Lei dos Nós
Esta lei segue da conservação de carga. A figura 2 mostra a junção de
três fios conduzindo correntes I1, I2 e I3. Como a carga não é criada nem
acumulada neste ponto, a conservação de carga conduz à lei dos nós
que, para este caso, é
I1 = I 2 + I 3
Figura 2
Resolução
(a) Seja I1 a corrente fornecida pela bateria esquerda, I2 a corrente fornecida pela
bateria direita e I3 a corrente que passa pelo resistor de 6Ω.
Figura 3
Podemos aplicar a Lei dos Nós na junção a.
I1 + I 2 = I 3
Eq.(1)
Podemos aplicar a Lei das Malhas à malha que envolve o circuito todo.
12,0 V – (4,0 Ω) * I1 + (3,0 Ω) * I2 – 12,0 V = 0
Eq.(2)
Podemos também aplicar a Lei das Malhas à malha localizada no braço
esquerdo do circuito.
12,0 V – (4,0 Ω) * I1 – (6,0 Ω) * I3 = 0
Eq.(3)
Resolvendo um sistema de equações composto pelas equações (1), (2) e (3) é
possível encontrar o valor das correntes.
I1 = 0,667 A
I2 = 0,889 A
I3 = 1,56 A
(b) Aplicando a lei de Ohm podemos encontrar a diferença de potencial entre os
pontos a e b.
Vab = R * I3
Vab = (6,0 Ω) * (1,56 A)
Vab = 9,36 V
(c)Podemos expressar a potência fornecida pela bateria no braço esquerdo do
circuito.
Pesq = ε * I1
Pesq = (12,0 V) * (0,667 A)
Pesq = 8,0 W
Podemos também expressar a potência fornecida pela bateria no braço direito
do circuito.
Pdir = ε * I2
Pdir = (12,0 V) * (0,889 A)
Pdir = 10,7 W