Exponencial de Matrizes

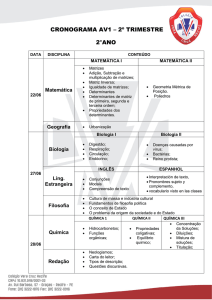
[Indíce]
[Introdução]
[Descrição do ficheiro ExpMatriz.MTH e exemplos]
[Listagem do ficheiro ExpMatriz.MTH]
[Agradecimentos e Referências]
2. Exponencial de matrizes
Seja A uma matriz quadrada de ordem n, de coeficientes complexos. Para
 n n
t A
qualquer número real t, a série 
é (absolutamente) convergente, pelo que
n  0 n!
 n n
t A
podemos definir uma função de variável real pondo e tA  
. Prova-se que esta
n  0 n!
função é diferenciável em qualquer ponto do seu domínio e que  e tA   Ae tA . Mais
precisamente, tem-se o seguinte resultado:
'
Teorema 1
Sejam A e B matrizes quadradas de ordem n. Então F( t )  e tA B é a única solução do
problema de valor inicial
F'( t )  AF( t ), F( 0)  B, para t  R
Demonstração: ver, por exemplo, Ap2.
Observação:
A exponencial assim definida tem muitas propriedades em comum com a função
exponencial usual: por exemplo, e ( t s) A  e tA e sA . Não é, no entanto, válido que
e A  B  e A e B para matrizes A e B quaisquer (apresentaremos mais adiante um contraexemplo), embora isto seja válido se AB  BA.
A solução do sistema homogéneo de equações diferenciais lineares de
coeficientes constantes definido por X'( t )  AX( t ) com condição inicial
X(0)  X 0 , onde X 0 é um vector de dimensão n, é dada pois por X( t )  e tA X 0 . Daqui
resulta a enorme importância de dispôr de processos práticos para calcular e tA . É
imediato constatar que o cálculo directo a partir da série definidora é, em geral,
impraticável, a não ser em casos muito particulares (matrizes diagonais, por exemplo).
Começaremos por demonstrar uma proposição simples que vai permitir resolver o
problema para matrizes 2x2 e 3x3.
Em tudo o que se vai seguir, consideraremos sempre as matrizes sobre o corpo
complexo, ainda que os seus coeficientes sejam reais. Assim, os valores próprios
coincidem com as raízes (em C) do polinómio característico. Diremos que um valor
próprio é simples, duplo, triplo,.... quando ele for raíz simples, dupla, tripla,... do
polinómio característico; quando falarmos da multiplicidade de um valor próprio,
estaremos sempre a considerar a multiplicidade algébrica. Adoptamos ainda a
convenção de que o grau do polinómio idênticamente nulo é   .
Teorema 2
Seja A uma matriz de ordem n. Então:
a) se todos os valores próprios de A são iguais a  tem-se
n 1 k
t
k
e tA  et  A  Id n  .
k 0 k !
b) se A tem n valores próprios distintos  1 ,  2 , n , então
n
e tA  e t  e  k t L k (A ),
k 1
n
sendo L k (A)  
j1
j k
A   j Id n
k  1, 2,, n.
k   j
c) se A tem 2 valores próprios distintos,  e , de multiplicidades n  1 e 1,
respectivamente, vem
k
n2
 t
tk
k
k t  A  Id n 
t
t
 e  A  Id n   e  e      
k !       n 1
k 0 k !
k 0

n 1
n2
e tA
.
Demonstração:

tk
(A  Id n ) k ; como o polinómio característico de A é
k
!
k 0
a) e tA  e t e t ( A Id n )  e t 
  1 n  x   n , segue-se que A  Id n   0, se k  n , pelo teorema de Cayleyk
Hamilton, donde o resultado.
n
b) Seja F( t )   e  k t L k (A ) ; vamos ver que F é solução do problema de valor inicial
k 1
X'  AX
, donde se seguirá que F( t )  etA , pelo teorema 1.

X
(
0
)

Id
n

Tem-se AF( t )  F' ( t )   e  k t A   k Id n L k (A ) ; como o polinómio característico de
n
k 1
A é   1  x   1  x   2  x   n  , segue-se que A   k Id n L k (A)  0 , para
k  1, 2, , n pelo teorema de Cayley-Hamilton, donde F'( t )  AF( t ) . Falta só provar
n
n
que F( 0)  Id n , ou seja, que
L
k 1
k
(A )  Id n .
Considerem-se
os
polinómios
em
x
definidos
por
n
xj
L k ( x)  
k  1, 2,, n ; é imediato que se trata de polinómios em x de
j1  k   j
j k
grau n  1 , que verificam Lk ( i )  0 se i  k e L k (  i )  1 se i  k . Conclui-se que
n
P ( x)  1   Lk ( x) é um polinómio de grau menor ou igual a n  1 que tem n raízes
k 1
distintas  1 ,  2 , ,  n e é pois idênticamente nulo. Portanto, P( A)  0 e logo
n
L
k 1
k
(A )  Id n , como queríamos.
c) Tem-se que:
e
tA
t
e e
t ( A  Id n )

tk
 e  (A  Id n ) k 
k 0 k !
t

tk
tk
k
t
 e  (A  Id n )  e  (A  Id n ) k 
k 0 k !
k  n 1 k !
t
n2
(*)

tk
t n 1 i
k
t
 e  (A  Id n )  e 
(A  Id n ) n 1 i .
k 0 k !
i  0  n  1  i !
t
n2
Como
A  Id n  A  Id n      Id n ,
conclui-se que
A  Id  A  Id   A  Id      A  Id 
n 1
n
n
n
n
n
n 1
;
como o polinómio característico de A é   1  x    x   , segue-se que o
primeiro membro desta igualdade é nulo (pelo teorema de Cayley-Hamilton), donde
n
A  Id      A  Id  . Por aplicação
A  Id       A  Id  e portanto
n 1
n
n
n
n 1 i
n
n 1
repetida desta fórmula, vem que
n 1
i
n

t n 1 i
t n 1 i
i
n 1 i
(A  Id n )

    (A  Id n ) n 1 






i0 n  1  i !
i0 n  1  i !

n 1 
n 1

     t n2 t k
tk
k ( A  Id n )
k  ( A  Id n )


 
 e
      
.
   
n 1
n 1
     
 
k  n 1 k !
k 0 k !
    

Substituindo esta fórmula na última linha de (*), segue-se o resultado.
O teorema 2 resolve completamente o problema do cálculo de e tA para matrizes
2x2 e 3x3. Para matrizes 2x2, os resultados das duas primeiras alíneas são suficientes:
uma matriz 2x2 ou tem um valor próprio duplo ou dois valores próprios distintos; no
primeiro caso, aplica-se a fórmula da alínea a) e no segundo a fórmula da alínea b).
Passando às matrizes 3x3, há três hipóteses a considerar:
1. a matriz tem um valor próprio triplo; usa-se a fórmula da alínea a).
2. a matriz tem três valores próprios distintos; usa-se a fórmula da alínea b).
3. a matriz tem um valor próprio duplo  e um valor próprio simples ; usa-se a
fórmula da alínea c).
Exercício
1 1
Sejam A  
 e B
 0 0
1  1
A B
AB
0 0 . Mostre que e e  e .


O caso das matrizes 4x4 é mais complicado. Há cinco hipóteses distintas:
1. a matriz tem um valor próprio quádruplo; usa-se a fórmula da alínea a).
2. a matriz tem quatro valores próprios distintos; usa-se a fórmula da alínea b).
3. a matriz tem um valor próprio triplo  e um valor próprio simples ; usa-se a fórmula
da alínea c).
4. a matriz tem dois valores próprios simples,  e  e um valor próprio duplo .
5. a matriz tem dois valores próprio duplos,  e .
Para tratar estes dois últimos casos, vamos utilizar um método geral para o
cálculo da exponencial de matrizes: o método de Putzer. Este método tem a vantagem
de ser elementar, não requerendo conhecimentos para além dos referidos na Introdução,
ao contrário do que sucede com o “método do polinómio” descrito em WA ou com os
processos baseados na forma canónica de Jordan.
Teorema 3 (método de Putzer)
Seja A uma matriz quadrada de ordem n e  1 ,  2 , ,  n os seus valores próprios,
repetidos de acordo com as suas multiplicidades. Então
n 1
e tA   rk 1 ( t ) Pk  A 
k 0
onde P0  A  Id n , Pk  A  Pk 1 A A   k Id n , para k  1, 2,, n  1 e r1 t ,rn  t 
são as soluções dos problemas de Cauchy
 r1'   1 r1
r1 (0)  1
 '
 rk 1   k 1 rk 1  rk rk 1  0  0,
k  1,, n  1
.
Demonstração:
Segue-se um método muito semelhante ao usado na prova da alínea b) do teorema 2.
n 1
Seja F( t )   rk 1 ( t ) Pk  A  ; como é evidente que F( 0)  Id n , basta provar que
k 0
F ( t )  AF( t ) para obter o resultado.
Se definirmos r0  0 , vem
'
n 1
n 1
F ' ( t )   rk' 1 ( t ) Pk (A )    rk ( t )   k 1 rk 1 ( t )Pk (A ) 
k 0
k 0
n2
n 1
k 0
k 0
  rk 1 ( t ) Pk 1 (A )    k 1 rk 1 ( t ) Pk 1 (A )
donde F ( t )   n F( t ) 
'
n 2
r
k0
k 1
( t ) Pk 1 ( A )  ( k 1   n ) Pk ( A ) .
Como Pk 1  A  A   k 1Id n Pk  A , segue-se que
Pk 1 ( A )  ( k 1   n ) Pk ( A )   A   n Id n Pk ( A ).
Substituindo esta igualdade na expressão obtida para F ' ( t )   n F( t ), vem :
n2


F ( t )   n F( t )  A   n Id n  rk 1 ( t ) Pk (A) A   n Id n  F( t )  rn ( t ) Pn 1 (A) 
'
k 0
 A   n Id n F( t )  rn ( t ) Pn (A)
Pelo teorema de Cayley-Hamilton, Pn ( A )  0 e vem F' ( t )   n F( t )  AF( t )   n F( t ) ,
donde F' ( t )  AF( t ) , como queríamos.
Observações
1) Pelo teorema anterior, podemos concluir que, dada uma matriz quadrada A de ordem
n, e tA pode ser escrito como um polinómio em A, de grau menor que n e cujos
coeficientes são funções escalares de t. Este resultado pode ser demonstrado
directamente, sem recurso ao método de Putzer (ver CF), mas a demonstração aí
apresentada não leva a um método prático para o cálculo dos coeficientes.
2) As equações diferenciais verificadas pelos coeficientes rk  t  são muito simples:
lineares, de primeira ordem e coeficientes constantes. O problema é que, para k>1,
são não homogéneas, e os seus segundos membros tornam-se cada vez mais
complexos, à medida que k aumenta.
Vejamos agora como resolver o quarto caso do cálculo de e tA para matrizes
quadradas 4x4. A matriz em causa tem dois valores próprios simples,  e  e um valor
próprio duplo . Pelo método de Putzer, devemos considerar o sistema







r1'  r1 ,
r2'  r2  r1 ,
r3'  r3  r2 ,
r4'  r4  r3 ,
r1 (0)  1
r2  0  0
r3  0  0
r4  0  0
As duas primeiras equações são muito fáceis de resolver: obtem-se r1 ( t )  e t e
1
r2 ( t ) 
e t  e t  , respectivamente. A terceira já é má e a quarta muito pior. Uma

maneira de evitar os cálculos extremamente aborrecidos necessários à sua resolução é
utilizar o DERIVE. Para isso, basta abrir a utility file ODE1.MTH, contendo funções
que permitem resolver simbolicamente uma larga gama de equações diferenciais de
primeira ordem. A função que nos interessa é LINEAR1(p, q, x, y, x0,y0), que dá a
solução da equação y'  p( x) y  q ( x) , com a condição inicial y0  y( x0). Basta então
copiar esta função para um novo ficheiro e proceder como indicado na listagem a seguir
para se obter r3 ( x).
Analogamente se obtém r4 :
2
r4 ( t ) 

e t      e t      e t      t  t  1  1  t    t  2
2
          
2

2
Finalmente, vejamos resumidamente como resolver o quinto caso para matrizes
4x4. Sejam  e  os dois valores próprios duplos. O sistema a considerar é







r1'  r1 ,
r2'  r2  r1 ,
r3'  r3  r2 ,
r4'  r4  r3 ,
r1 (0)  1
r2  0  0
.
r3  0  0
r4  0  0
A solução pode obter-se tal como para o quarto caso, eventualmente recorrendo
ao DERIVE para evitar os cálculos mais morosos. Limitamo-nos a indicar os resultados:
r1 ( t )  e t
r2 ( t )  te t
r3 ( t ) 
r4 ( t ) 
e t  t  t  1  e t
   
2
e t  t  t  2  e t  t  t  2
[Anterior]
[Próximo]
   
3
.