Pitagoras – Bombons – Tabuleiros

Pitágoras – Bombons e tabuleiros.
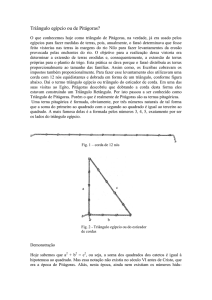
Pitágoras ficou muito conhecido pelo teorema que leva seu nome, talvez esse seja o teorema
mais conhecido da matemática. O teorema de Pitágoras. De acordo com este teorema, em um
triângulo retângulo, a soma do quadrado dos catetos é igual ao quadrado da hipotenusa. A
demonstração geométrica do teorema - existem numerosas maneiras de demonstrá-lo - muito
provavelmente não era do tempo de Pitágoras, embora certamente ele conhecesse os
triângulos retângulos e a relação existente entre os seus lados.
A matemática de Pitágoras era uma matemática de pontinhos. Os números, por assim dizer,
não representavam exatamente uma quantidade, mas uma configuração de pontos. Como os
grãos de areia numa praia, ou as estrelas no céu. Ainda que seja muito difícil contá-las, na
medida em que podem ser delimitadas, é como se o número fizesse parte delas.
A matemática de Pitágoras era uma gostosa matemática das caixas de bombons. Aquelas em
que os bombons vêm organizados em fileiras, cada um em seu lugar. Pitágoras gostava das
caixas de bombons triangulares e também quadradas.
As caixas de bombons triangulares têm 1, 3, 6, 10, 15... bombons. Elas vão ficando maiores, na
medida em que são adicionados números em sequência:
1;
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
Os caixas de bombons quadradas são também boas de matemática.
Estas caixas são interessantes, para aumenta-las, cada vez soma-se um número ímpar, em
sequência:
1
1+3=4
1+3+5=9
1+3+5+7=16
1+3+5+7+9=25
Os números quadrados são efetivamente números quadrados, elevados ao quadrado
(potência de 2):
12=1
22=4
32=9
42=16
52=25
Algumas coisas interessantes acontecem na matemática, que às vezes espantam como são
regulares, eu não podia imaginar que um número quadrado era formado de números ímpares,
somados em sequência. E para a gente “pular” de um número quadrado ao próximo, é só
somar um número ímpar em sequência:
1+3=4
4+5=9
9+7=16
16+9=25
É só ver na figura como fazer para crescer a caixa de bombom quadrada.
Pitágoras era um cara amigo dos números. Talvez visse neles gostosos bombons, em caixas
cuidadosamente ordenadas.
Foi cuidando de seus números quadrados que ele encontrou um aspecto curioso: às vezes, um
número quadrado era formado pela soma de dois outros números quadrados. A interessante
caixa de 25 bombons “cabia” exatamente os bombons das caixas de 9 e 16 bombons.
9+16=25
32+42=52
Esses três números, 3, 4 e 5, ficaram então conhecidos como uma das tríades pitagóricas, que
são os lados de um triângulo que satisfazem as condições algébricas do que ficou
posteriormente conhecido como o teorema “de Pitágoras”: a2=b2+c2
Outras tríades pitagóricas:
 25+144=169  52+122=132
 49+576=652  72+242=252
 81+1600=1681  92+402=412
 121+3600=3721  112+602=612
A matemática de pontinhos de Pitágoras não pode ser transferida sem problemas para uma
concepção geométrica “Euclidiana”. Isso é particularmente evidente com os números
triangulares, embora menos problemático com os números quadrados.
Nos números triangulares, se tivermos 3 bombons num dos lados do triângulo, o número de
bombons será 6. Se o lado tiver 4, o número de bombons será 10. Não há, digamos assim, uma
correspondência entre o triângulo equilátero, como uma figura geométrica, e o número
triangular, embora isso ocorra com o número quadrado.
Em quadrado, calculamos a área pelo quadrado do lado, do mesmo modo que calculamos o
número de bombons de uma caixa quadrada, sabendo o número de bombons de um dos lados
da caixa.
Um aspecto interessante de número triângulos e quadrados, é que a soma de dois números
triângulos sucessivos dá um número quadrado.
É fácil de ver, se dividimos um número quadrado em dois números triângulos:
É fácil de ver como o quadrado de lado 4 é formado pelos números triângulos sucessivos, de
lado 3 e 4.
Já dá para vez como isso é geometricamente estranho. Dois triângulos equiláteros formam um
losango, não um quadrado.
É um estranho enigma. Uma solução que encontrei foi pensar no número quadrado agora não
mais como uma caixa de bombons, mas como um tabuleiro de damas:
Aqui dá para ver que o número triângulo 7 somado ao número triângulo 8 dá o número
quadrado 8.
O número triângulo, na concepção Pitagórica, é então um triângulo retângulo isósceles, e a sua
área aproximada é dada por base x altura /2 ficando de fora parte das casas do tabuleiro.
A área do quadrado o tabuleiro como um todo é 8x8=64
O triângulo retângulo isósceles de cateto = 7 tem área de 7x7/2= 49/2=24,5
O triângulo retângulo isósceles de cateto = 8 tem área de 8x8/2= 64/2=32
Uma parte do tabuleiro, entre as duas linhas vermelhas (vou chamar de x) não entra nesta
conta:
24,5+32+x=64
56,5+x=64
x=64-56,5
x=7,5
Se eu for aumentando o número dos quadrados, a distância entre as duas linhas vermelhas vai
diminuir, o meu número triângulo vai se aproximar cada vez mais o triângulo geométrico:
Aqui o número triângulo 15 somado ao número triângulo 16 dá o número quadrado 16:
Para um tabuleiro de 162casas (=256 casas), a faixa entre as linhas vermelhas vai ser de 15,5.
Na medida em que as casas do tabuleiro ficam menores, as linhas vermelhas vão se
aproximando, no número quadrado de lado 32, formado pela soma de números triângulos 31
e 32:
Nesse tabuleiro de 322 casas (=1024 casas) a faixa entre as linhas vermelhas é de 31,5.
Na medida em que aumentam o número de casas do tabuleiro e elas diminuem em tamanho,
as linhas vermelhas se aproximam, representando parcelas cada vez menores do tabuleiro
como um todo.
A matemática de hoje não incorpora o uso de “pontinhos”; a noção de número tem muito
mais um significado abstrato, e as relações são descritas muito mais em termos algébricos, do
que figurativamente, como Pitágoras parecia fazer com suas caixas de bombons (e eu com os
tabuleiros).
O número triângulo, como vimos, é uma sequência aritmética, produzida pela adição de
números sucessivos:
1, 3, 6, 10, 15, 21,
O número de pontinhos, n, para um dado triângulo vai ser dado pela fórmula algébrica:
Nós já vimos que se somarmos dois números triângulos consecutivos vai dar um número
quadrado (por exemplo, 3+6=9; 6+10=16). Então, o dobro do número triângulo é igual ao
número quadrado mais um dos lados (é só mudar um pouco a fórmula, para ver):
Vamos somar dois triângulos consecutivos, para chegar a um número quadrado:
A matemática de pontinhos não corresponde diretamente à matemática geométrica. Os
pontinhos de Pitágoras são unidades discretas, diferente do ponto geométrico, que não tem
medida, ou dimensão, ou seja, é infinitamente pequeno.
Se levarmos adiante aquela brincadeira de dividir o tabuleiro em quadrados cada vez menores,
nos aproximaremos cada vez mais do ponto geométrico, mas sempre será possível dividir mais
ainda, e ficaremos mais perto, mas ainda poderemos dividir mais, e isso não terá fim.
Chegaremos muito próximo do zero. O zero, digamos, é o limite, zero é o que não pode mais
ser dividido.
Neste ponto, a matemática de pontinhos de Pitágoras vai ser bem próxima da matemática
geométrica:
A área do triângulo dada pela matemática de pontinhos:
Vai ser bem próxima da área calculada pela geometria:
Ou seja, a razão entre as duas fórmulas, vai se aproximar de 1, na medida em que cresce o
valor de L:
(
)
Esta estranha brincadeira parece sugerir que o ponto matemático, não se representa por
pequeno ponto de bordas arredondadas, mas teria certa quadratura, de modo que se pudesse
ocupar o espaço, sem possibilitar a existência de vazios.