Triângulo egípcio ou de Pitágoras?

Triângulo egípcio ou de Pitágoras?
O que conhecemos hoje como triângulo de Pitágoras, na verdade, já era usado pelos
egípcios para fazer medidas de terras, pois, anualmente, o faraó determinava que fosse
feito vistorias nas terras às margens do rio Nilo para fazer levantamentos da erosão
provocada pelas enchentes do rio. O objetivo para a realização dessa vistoria era
determinar a extensão de terras erodidas e, consequentemente, a extensão de terras
próprias para o plantio de trigo. Esta prática se dava porque o faraó distribuía as terras
proporcionalmente ao tamanho das famílias. Assim como, os Escribas cobravam os
impostos também proporcionalmente. Para fazer esse levantamento eles utilizavam uma
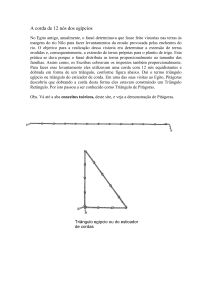
corda com 12 nós equidistantes e dobrada em forma de um triângulo, conforme figura
abaixo. Daí o termo triângulo egípcio ou triângulo do esticador de corda. Em uma das
suas visitas ao Egito, Pitágoras descobriu que dobrando a corda desta forma eles
estavam construindo um Triângulo Retângulo. Por isto passou a ser conhecido como
Triângulo de Pitágoras. Porém o que é realmente de Pitágoras são as ternas pitagóricas.
Uma terna pitagórica é formada, obviamente, por três números naturais de tal forma
que a soma do primeiro ao quadrado com o segundo ao quadrado é igual ao terceiro ao
quadrado. A mais famosa delas é a formada pelos números 3, 4, 5, exatamente por ser
os lados do triângulo egípcio.
Fig. 1 – corda de 12 nós
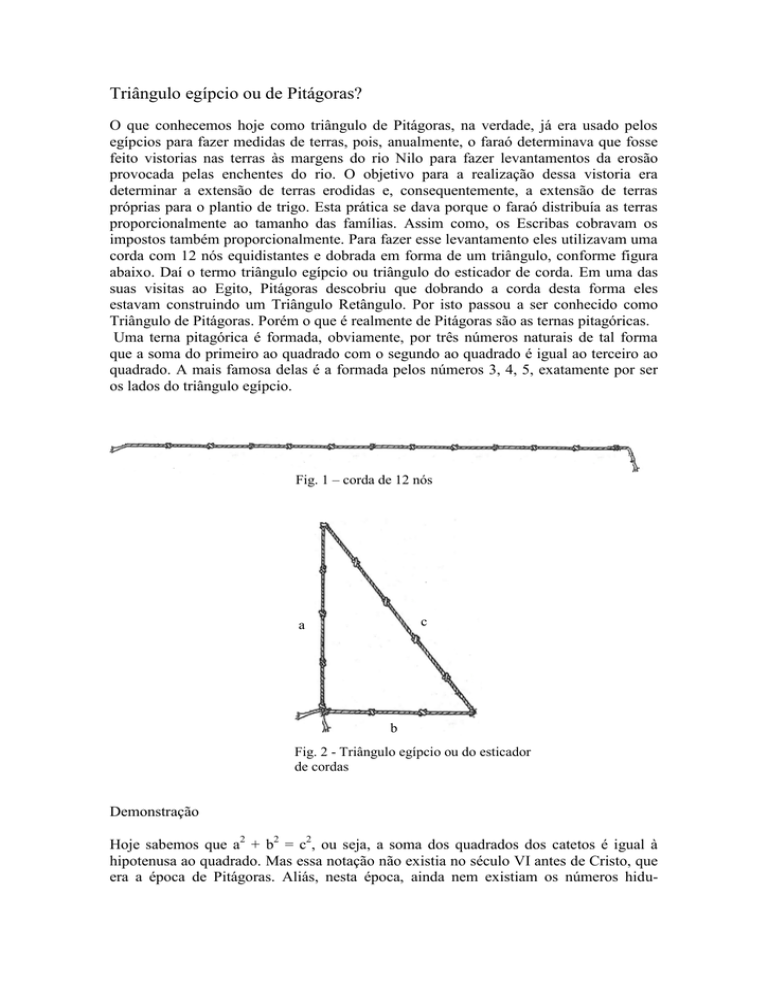
c
a
b
Fig. 2 - Triângulo egípcio ou do esticador
de cordas
Demonstração
Hoje sabemos que a2 + b2 = c2, ou seja, a soma dos quadrados dos catetos é igual à
hipotenusa ao quadrado. Mas essa notação não existia no século VI antes de Cristo, que
era a época de Pitágoras. Aliás, nesta época, ainda nem existiam os números hidu-
arábicos e esta notação surge somente no século XVII com René Descartes. Então,
como Pitágoras fez?
Bem, para se constituir num triângulo retângulo, é necessário que o ângulo formado
pelos lados a e b (catetos), seja um ângulo reto, ou de 90°. Para que ocorra essa
situação, é necessário que estes lados sejam perpendiculares entre si. Percebendo essa
condição, Pitágoras criou quadrados a partir de cada lado do retângulo e subdividiu
esses quadrados em pequenos quadrados de lados iguais à distância entre um nó e outro,
conforme figura 3. Perceba o leitor, que, junto ao cateto a formam-se 16 quadrados,
junto ao cateto b formam-se 9 quadrados e junto à hipotenusa formam-se 25 quadrados.
Aí está a prova que
a2 + b2 = c2
Fig. 3 – Demonstração de Pitágoras da sua primeira terna (3, 4, 5)