β - MAT-UFG

Aspectos Matemáticos e
Históricos Pertinentes ao
Regulador Centrı́fugo de Watt
para a Máquina de Vapor
Jorge Sotomayor
Universidade de São Paulo
http://www.ime.usp.br/˜sotp/
Goiânia, Novembro, 2006
Programa para esta Palestra
• Alguns Marcos de Referência.
• Equações Diferenciais do Regulador.
• Revisitando Maxwell e Vishnegradskii
com Pontryagin .
• Além da Primeira Bifurcação
• Bifurcações e Fatos Novos.
• Recap. e Comentários: O Futuro?
• Referências Bibliográficas
1
I. Alguns Marcos de Referência
• O trabalho nos tempos antigos baseava-se
na:
- força muscular
- rodas movidas pelas águas
- moinhos de vento
Estes controlados pela intervenção HUMANA.
• Um evento NOTÁVEL aconteceu com a
invenção do instrumental para o CONTROLE AUTOMÁTICO — A AUTO REGULAÇÃO— da força do vapor, um passo
fundamental para o sucesso econômico da
REVOLUÇÃO INDUSTRIAL NO SÉCULO
XVIII, na Inglaterra.
2
Força Muscular e do Vento
————————————————–
Controle pela Mão Humana
3
Moinho Hidráulico, Fonte Wikipedia
4
Moinho de Vento com Controle Direcional
5
Moinho de Vento, Diagrama Interno
6
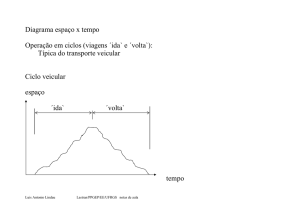
O regulador centrı́fugo de Watt é um dispositivo que controla automaticamente a velocidade de rotação de uma máquina a vapor.
Sua invenção data de 1788 e pode ser tomada
como ponto de partida para a TEORIA DE
CONTROLE AUTOMÁTICO, i.e., sem a intervenção direta da mão humana.
Sistema Máquina de Vapor - Regulador de
Watt
7
Escultura
Máquina de de Watt
Aprimoramentos na arquitetura e desenho do
regulador, ocorridos na primeira metade do séc.
XIX, levaram a produtos menos confiáveis cujo
desempenho passou a ser OSCILATÓRIO ou
mesmo ERRÁTICO em lugar do ideal de velocidade CONSTANTE.
8
Marcos de Referência e Contemporâneos
• Watt, 1788
Adam Smith e a Teoria Econômica
• Maxwell, 1868
Airy
Routh e a Estabilidade
• Vyshnegradskii, 1877
Stodola, Hurwitz
• Pontryagin, 1962
Andronov,
Estabilidade Estrutural,
Bifurcações
9
II. Equações Diferenciais de Pontryagin
dϕ
= ψ
dτ
dψ
g
b
2
2
= c Ω sin ϕ cos ϕ − sin ϕ −
ψ
dτ
l
m
1
dΩ
=
(µ cos ϕ − F )
dτ
I
0, π2
ϕ∈
— ângulo de abertura dos braços do
regulador a partir de seu eixo vertical S1,
Ω ∈ [0, ∞) — velocidade angular de rotação
do volante D, com momento de inércia I,
τ — tempo,
ψ = dϕ/dτ ,
θ — velocidade angular de S1,
θ = c Ω, c > 0 — razão de transmissão,
10
H — camisa mecânica que suporta os braços
do regulador e pode deslizar ao longo de S1,
T — conjunto de engrenagens,
V — válvula que determina a quantidade de
vapor para a máquina,
l — comprimento dos braços do regulador,
m — massa de cada contrapeso esférico,
g — aceleração da gravidade,
b > 0 — constante da força atrito,
F — torque equivalente da carga mecânica,
µ > 0 — uma constante de proporcionalidade.
11
III. Os aspectos Matemáticos desta palestra
referem-se a um relato de nosso estudo, desenvolvido em colaboração com L.F. Mello e
D. Braga, da Estabilidade e Bifurcações dos
pontos de equilı́brio das Equações Diferenciais
de Pontryagin
Realizando as seguintes mudanças nas coordenadas e no tempo
s
x = ϕ, y =
l
ψ, z = c
g
s
l
Ω, τ =
g
s
l
t,
g
as equações de Pontryagin —SRW— se escrevem como
dx
= y
dt
dy
y0 =
= z 2 sin x cos x − sin x − ε y
dt
dz
z0 =
= α (cos x − β )
dt
x0 =
12
dependendo dos parâmetros normalizados
ε > 0, α > 0, 0 < β < 1,
dados por
b
ε=
m
s
l
clµ
F
, α=
, β= .
g
gI
µ
SRW é uma famı́lia a 3 parâmetros de equações
diferenciais
x0 = f (x, ζ),
f (x, ζ) =
y, z 2 sin x cos x − sin x − εy, α
(cos x − β ) ,
π
x = (x, y, z) ∈ 0,
× R × [0, ∞),
2
ζ = (β, α, ε) ∈ (0, 1) × (0, ∞) × (0, ∞) .
13
SRW tem apenas um ponto de equilı́brio
s !
1
.
β
P0 = (x0, y0, z0) = arccos β, 0,
A matriz Jacobiana de f em P0 é






Df (P0) = 




0
1 − β2
−
β
q
−α 1 − β 2
1
0
0
0




q

2
−ε 2 β(1 − β ) 





e seu polinômio caracterı́stico p(λ)
−p(λ) =
λ3 + ε λ2 +
1 − β2
1 − β2
3/2
λ+2αβ
.
β
β
14
IV. Teorema do livro de Pontryagin e Primeiro
Coeficiente de Lyapunov l1
Para todo
ε > 2 α β 3/2
SRW tem P0 como um ponto de equilı́brio assintoticamente estável.
Para 0 < ε < 2 α β 3/2, P0 é instável (sela).
A superfı́cie de parâmetros crı́ticos — superfı́cie
de bifurcação — Σ1 é
εc = ε(β, α) = 2 α β 3/2.
15
Superfı́cie Σ1
DESCREVER a mudança na estabilidade do
equilı́brio P0 quando os parâmetros intersectam a superfı́cie Σ1 é o principal objetivo desta
apresentação.
16
Bifurcação de Hopf
17
Artigos anteriores sobre o estudo da bifurcação
de Hopf sobre Σ1:
Estudo numérico da bifurcação de Hopf:
B. D. Hassard, N. D. Kazarinoff and Y. H.
Wan, Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge,
1981.
Estudo analı́tico da bifurcação de Hopf mas
pouco conclusivo a respeito do sinal de l1:
A. Al-Humadi and N. D. Kazarinoff, Hopf bifurcation in the Watt steam engine, Bull. Inst.
Math. Appl., 21 (1985), 133-136.
18
Um estudo sobre a bifurcação de Hopf de codimensão 1 em SRW está em:
J. Sotomayor, L. F. Mello and D. C. Braga,
Stability and Hopf bifurcation in the Watt governor system, Commun. Appl. Nonlinear Anal.,
13 (2006), 1-17.
http://arxiv.org/abs/math.DS/0606230.
Um estudo mais geral sobre a bifurcação de
Hopf até a codimensão 3 em SRW está em:
J. Sotomayor, L. F. Mello and D. C. Braga,
Bifurcation analysis of the Watt governor system, aceito para publicação em Comp. Appl.
Math. (2006).
http://arxiv.org/abs/math.DS/0604177.
19
Encontramos uma EXPRESSÃO SIMPLES para o PRIMEIRO COEFICIENTE DE LYAPUNOV – l1 – sobre Σ1, seu sinal e a curva onde
ele se anula Σ2:
Teorema (Sotomayor, Mello, Braga). O primeiro coeficiente de Lyapunov para P0 em um
ponto de Σ1 é dado por
l1 = −
3/2
2
2
2
4
6
αβ
(1 − β ) 3 + (α − 5)β + α β
.
2
2
4
2
2
4
2 1−β +α β
1 − β + 4α β
Se
g(β, α) = 3 + (α2 − 5)β 2 + α4β 6
é diferente de zero, então SRW tem um ponto
de Hopf transversal — H1 — em P0.
20
Se (β, α, εc) ∈ S ∪ U então SRW tem um ponto
de Hopf H1 em P0. Se (β, α, εc) ∈ S então
o ponto H1 em P0 é assintoticamente estável
e para cada ε < εc, mas próximo de εc, existe
uma órbita periódica estável perto do equilı́brio
instável P0.
Se (β, α, εc) ∈ U então o ponto de Hopf H1 em
P0 é instável e para cada ε > εc, mas próximo
de εc, existe uma órbita periódica instável perto
do equilı́brio assintoticamente estável P0.
21
Curta nota biográfica sobre Pontryagin Em
1952 Pontryagin, originalmente renomado topólogo, começou a estudar problemas de matemática aplicada, enfocando as equações diferenciais e a teoria do controle. Esta virada não
era inesperada. De fato, nos anos 30 Pontryagin fez amizade com o fı́sico A. A. Andronov e
com ele passou a discutir problemas nas teorias das oscilações e do controle automático,
nos quais Andronov trabalhava.
L. S. Pontryagin (1908–1988)
22
Na sua vibrante autobiografia cientı́fica (Russian Math. Surveys, 33:6 (1978)) ele escreve :
“ Certo dia, em 1932 eu acho, um jovem fı́sico
chamado Aleksandr Aleksandrovich Andronov,
a quem eu não conhecia até esse momento,
chegou a meu apartamento sem haver-se previamente anunciado. Ele me disse que havia
ouvido falar de meu interesse em trabalhar em
problemas matemáticos aplicados e que gostaria
de contar-me algo. Foi dele que pela primeira
vez ouvi dizer o que é um retrato de fase e o
que são os ciclos limite, além de outras coisas
semelhantes. Ele argumentou que tudo isto é
aplicável a várias partes da tecnologia e, em
particular, à teoria das oscilações. Foi assim
que uma amizade sólida nasceu entre Andronov
e eu, a qual durou por vinte anos, até seu falecimento. Durante todos esses anos fui consultor
matemático de Andronov....”
23
“ ... a influência que Andronov teve em mim
redirecionaram meus interesses matemáticos.
Como resultado abandonei meu trabalho em
problemas de matemática abstrata.
... Estudei sistemas dinâmicos próximos de
Hamiltonianos e participei de seu trabalho sobre Sistemas Estruturalmente Estáveis.”
Este trabalho foi publicado in 1937.
Em 1961 juntamente com seus estudantes V.
G. Boltyanskii, R. V. Gamkrelidze e E. F. Mishchenko escreveu o livro clássico A Teoria Matemática dos Processos Ótimos.
O livro Ordinary Differential Equations, já citado, foi traduzido para o Inglês em 1962.
Andronov, Lefschetz, Peixoto, Thom, ....
24
V. IDÉIAS GERAIS SOBRE AS BIFURCAÇÕES E FATOS NOVOS SOBRA A DINÂMICA DO REGULADOR
PONTOS DE EQUILÍBRIO
x0 = f (x, u, v, w, ...)
x, variável dinâmica, estado;
u, v, w, .., parâmetros de controle.
ÓRBITAS PERIÓDICAS,
HOMOCLÍNICAS
DIAGRAMA DE BIFURCAÇÃO E SUA COMPLEXIDADE CRESCENTE COM O NÚMERO
DE PARÂMETROS – MULTIPLICIDADE – A
DIMENSÃO DE x.
DOIS DIAGRAMAS PARA EQUILÍBRIOS, x
DIMENSÃO 1: CÚSPIDES, ANDORINHAS
25
Cúspide , Wolfram MathWorld
f (x, u, v) = x3 + vx + u
26
Seção da Andorinha, Wolfram MathWorld
f (x, u, v, w) = x4 + vx2 + ux + w, v = −1
27
Em IV ficou determinado o conjunto Σ2 ⊂ Σ1
onde o primeiro coeficiente de Lyapunov se anula, definido por g(β, α) = 0.
Teorema (Sotomayor, Mello, Braga). O segundo coeficiente de Lyapunov para P0 em um
ponto de Σ2 é dado por
α β 3/2 h(β, α)
,
l2(β, α, εc) =
2
2
4
36(9 − 9β + 4α β )h1(β, α)
onde
h1(β, α) = (1 − β 2 + α2β 4)3(1 − β 2 + 4α2β 4)3
28
Expressão de h numa página
− 216 − 54(−16 + 37α2)β 2 − 3α2(389
+ 180α2)β 4 − 36(150 − 1709α2 + 564α4)β 6
+ (11880 − 220113α2 + 111026α4 − 5533α6)β 8
− 6(1944 − 59747α2 + 36063α4 + 5186α6)β 10
+ (5616 − 310545α2 + 189480α4 + 279290α6
− 16022α8)β 12 + 2(−540 + 69732α2
− 32266α4 − 369482α6 + 9347α8)β 14
− α2(25647 + 3390α2 − 960987α4 − 151080α6
+ 21205α8)β 16
+ 2α4(2319 + 4α2(−79183 − 58517α2
+ 8384α4))β 18 − 2α6(−84400 − 251671α2
+ 31277α4 + 7208α6)β 20
+ 2α8(−94479 − 6748α2 + 23208α4)β 22
− α10(−31463 + 58672α2 + 4880α4)β 24
+ 16α12(1627 + 718α2)β 26
− 16α14(453 + 40α2)β 28 + 640α16β 30.
29
A figura a seguir apresenta uma sı́ntese geométrica do Teorema anterior. O sinal de h(β, α)
dá o sinal do segundo coeficiente de Lyapunov
l2 para P0: l2 < 0 sobre o arco aberto, denotado por C1, da curva Σ2 onde l1 = 0. Sobre
este arco um ponto tı́pico R é representado.
Ainda, l2 > 0 sobre o arco aberto, denotado
por C2, da curva Σ2. Este arco contêm um
tı́pico ponto denotado por T .
30
Teorema. Se (β, α, εc) ∈ C1 ∪ C2 então SRW
tem um ponto de Hopf transversal de codimensão 2 –H2– em P0. Se (β, α, εc) ∈ C2
então P0 é instável e o diagrama de bifurcação
é como no ponto T abaixo. Se (β, α, εc) ∈ C1
então P0 é assintoticamente estável e o diagrama de bifurcação é como no ponto R.
31
Diagrama de bifurcação em T
32
Diagrama de bifurcação em R
33
Teorema. (Sotomayor, Mello, Braga). Para
SRW existe um ÚNICO ponto Q = (β, α, εc),
com coordenadas
β = 0.86828033997971281542...,
α = 0.85050048430685017856...
e
εc = 1.37624106484659953171...
onde as curvas Σ2 (l1 = 0) and l2 = 0, sobre a
superfı́cie crı́tica Σ1, se intersectam e o fazem
transversalmente.
Além disto, para os valores dos parâmetros
em Σ3 = {Q} SRW tem um ponto de Hopf
transversal de codimensão 3 –H3– em P0 o
qual é instável, pois l3(Q) > 0. O diagrama
de bifurcação em Q está ilustrado nas figuras
a seguir.
34
Diagrama de bifurcação em Q
Diagrama de bifurcação em R1
35
Teorema. Suponha que o sistema
x0 = f (x, ζ), x = (x, y, z), ζ = (β, α, ε)
tenha equilı́brio x = 0 para ζ = 0 com autovalores λ2,3(ζ) = η(ζ) ± iω(ζ) e ω(0) = ω0 > 0,
η(0) = 0, l1(0) = 0, l2(0) = 0, onde l1(ζ) e
l2(ζ) são o primeiro e segundo coeficientes de
Lyapunov, respectivamente. Assuma que
l3(0) 6= 0, onde l3(0) é o terceiro coeficiente
de Lyapunov;
a aplicação ζ → (η(ζ), l1(ζ), l2(ζ)) é regular em
ζ = 0.
Então, pela introdução de uma variável complexa, o sistema acima, reduzido à famı́lia parâmetro dependente de variedades centrais, é
topologicamente equivalente a
w0 = (η + iω0)w + τ w|w|2 + νw|w|4 + l3w|w|6
onde η, τ e ν são parâmetros de desdobramento.
36
VI. Recapitulação e Conclusões
Para a famı́lia a 3 parâmetros de E.D.O. SRW,
que modela o acoplamento do Regulador de
Watt com uma máquina a vapor, foi encontrada uma estratificação Σ1 ⊃ Σ2 ⊃ Σ3 =
{Q} do espaço de parâmetros, de acordo com
a codimensão e o caráter da estabilidade do
equilı́brio P0 como um ponto de Hopf.
Cada estrato é determinado implicitamente e
o caráter da estabilidade é determinado pelo
sinal do coeficiente de Lyapunov.
O ponto Q tem coordenadas β = 0.8682..., α =
0.8505..., ε = 1.3762..., com terceiro coeficiente
de Lyapunov POSITIVO.
No interior de uma lı́ngua cuspidal sólida, “do
lado de cima” da superfı́cie Σ1, com vértice
em Q, um equilı́brio atrator e uma órbita periódica atratora coexistem.
37
—VOLTANDO AO PASSADO—
Para se ter uma idéia da repercussão e aplicabilidade da idéia de Watt, podemos citar que
existiam 75000 unidades construı́das, somente
na Inglaterra, nos 80 primeiros anos após sua
invenção. Dado de MacFarlane. (Referências
no final)
Máquina com regulador – Museu do Vapor,
Londres
38
Regulador de Watt – Museu do Vapor,
Londres
A IDÉIA DE AUTO-REGULAÇÃO POR REALIMENTAÇÃO —FEEDBACK— É BEM ANTERIOR A WATT. VER OBRA DE O. MAYR.
SUA IMPLEMENTAÇÃO NO PROGRESSO
DA TECNOLOGIA TEM SIDO ESTIMULADO
POR DESAFIOS ECONÔMICOS, INDUSTRIAIS E DE DEFESA.
39
Scientific American, setembro 1952
O PRESENTE – COMPUTADORES E CHIPS
O FUTURO? – DESAFIOS TECNOLÓGICOS?
– MAIS GLOBAL E MATEMÁTICO!
Poincaré, Hilbert.
40
VII. Referências Pertinentes
A. A. Andronov, E. A. Leontovich et al., Theory of Bifurcations of Dynamic Systems on a
Plane, Halsted Press, J. Wiley & Sons, New
York, 1973.
M. Denny, Watt steam governor stability, Eur.
J. Phys., 23 (2002), 339-351.
Y. A. Kuznetsov, Elements of Applied Bifurcation Theory, Springer-Verlag, New York, 2004.
Y. A. Kuznetsov, Numerical normalization techniques for all codim 2 bifurcations of equilibria
in ODE’s, SIAM J. Numer. Anal., 36 (1999),
1104-1124.
A. G. J. MacFarlane, The development of frequency - response methods in automatic control, IEEE T. Automat. Contr., AC-24 (1979),
250-265.
J. C. Maxwell, On governors, Proc. R. Soc.
London, 16 (1868), 270-283.
41
O. Mayr, The Origins of Feedback Control,
MIT Press, Cambridge, MA, 1970.
L. S. Pontryagin, Ordinary Differential Equations, Addison-Wesley Publishing Company Inc.,
Reading, 1962.
F. Takens, Unfoldings of certain singularities
of vectorfields: Generalized Hopf bifurcations,
J. Diff. Equat., 14 (1973), 476-493.
I. A. Vyshnegradskii, Sur la théorie générale
des régulateurs, C. R. Acad. Sci. Paris, 83
(1876), 318-321.
Página de L. F. Mello contendo arquivos usados na prova com auxilio computacional:
http://www.ici.unifei.edu.br/luisfernando/wgs
42