x - Univap

Exercı́cios de Cálculo Numérico
Zero de Função
1. Dê um exemplo de função f (x), que tenha pelo menos uma raiz, que não pode
ser determinada usando o Método da Bisseção.
2. Dê um exemplo de função f (x), que tenha pelo menos uma raiz, onde o Método
de Newton-Raphson não converge.
3. A equação x2 − 7x + 12 = 0 tem 3 e 4 como raı́zes. Considere a função de
iteração dada por ϕ(x) = x2 − 6x + 12. Determine o intervalo (a, b), onde
para qualquer que seja x0 escolhido a sequência xn+1 = ϕ(xn ) converge para a
raiz x = 3. Mostre que a convergência é quadrática.
4. Para determinar a raiz quadrada de um número c ≥ 0, basta resolver a equação
x2 −c = 0. É possı́vel determinar sua raiz quadrada usando a função de iteração
ϕ(x) = c/x. Justifique a resposta.
5. As funções de iterações ϕ1 (x) = x2 /2 − 2x + 4 e ϕ2 (x) = x2 /2 − 2.5x + 5, geram
sequências convergentes para a raiz x = 2, para qualquer aproximação inicial
x0 ∈ (1.5, 3). Qual das duas funções geram sequências mais rapidamente
convergente para esta raiz. Justifique a resposta.
6. Determine um intervalo (a, b) e uma função de iteração ϕ(x) associada, de tal
forma que ∀x0 ∈ (a, b) a função de iteração gere uma sequência convergente
para a(s) raiz(es) de cada uma das funções abaixo, usando o método iterativo
linear (MIL) com tolerância ² ≤ 1.10−3 .
√
(a) f1 (x) = x − e−x
(b) f2 (x) = ln(x) − x + 2
(c) f3 (x) = ex/2 − x3
(d) f4 (x) = sen(x) − x2
(e) f5 (x) = x/4 − cos(x)
7. Determine a(s) raiz(es) da função f1 (x), usando o método da Bisseção, Método
da Falsa posição e da Falsa posição modificada com tolerância ε = 1.10−3 .
Quantas iterações foram necessárias para cada um dos métodos.
8. Determine as raı́zes do exercı́cio (6), usando o Método de Newton-Raphson.
9. Determine as raı́zes do exercı́cio (6), usando o Método das Secantes.
10. Determine os pontos extremos do exercı́cio (6), usando o Método de NewtonRaphson.
11. Determine o ponto de intersecção entre as funções f1 (x) e f2 (x), f2 (x) e f3 (x)
e entre f1 (x), f2 (x) e f3 (x).
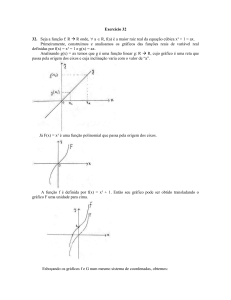
12. O Teorema do Valor Médio, diz que para função diferenciável f (x), existe um
número 0 < α < 1, tal que :
f (x) = f (a) + (x − a)f 0 (a + α(x − a))
Considere a = 0; α = 1/2 e f (x) = arctan(x). Determine o x > 0 que satisfaz
a igualdade acima.
13. Sabe-se que se x = ξ é uma raiz dupla de f (x) então o Método de NewtonRaphson não converge quadraticamente. Mostre que se
f 0 (ξ) = 0, mas todas as outras condições de convergência estão satisfeitas,
então a iteração:
2f (xn )
xn+1 = ϕ(xn ) = xn − 0
f (xn )
converge quadraticamente.
14. Seja x = ξ uma raiz de f (x), tal que f 0 (ξ) 6= 0 e f ”(ξ) = 0. Mostre que neste
caso o Método de Newton-Raphson tem convergência cúbica.
15. Encontre todas as raı́zes reais do polinômio abaixo pelo método de NewtonRaphson.
p(x) = x4 − 2x3 + 4x − 1.6
16. Uma pessoa tomou um empréstimo de A reais, que acrescenta os juros no total
antes de computar o pagamento mensal. Assim, se a taxa mensal de juros, em
porcentagem, é q e o empréstimo é pelo prazo de n meses, a quantia total que
o tomador concorda em pagar é:
C = A + A.n.
q
.
100
Isto é dividido por n para dar o total de cada pagamento P , ou seja
P =
³1
C
q ´
=A
+
n
n 100
Isto é perfeitamente legal e muito usado em lojas de departamento .( É chamado
o empréstimo com acréscimo). Mas a verdadeira taxa de juros que o tomador
está pagando é alguma coisa além de q%, porque ele não conserva o total do
empréstimo por todos os n meses: Ele está pagando-o de volta com o decorrer
do tempo. A verdadeira taxa de juros pode ser encontrada pela determinação
de uma raiz x da equação:
F (x) = (Ax − P )(1 + x)n + P = 0
Isto fornece a taxa de juros por perı́odo de pagamento, que pode ser convertida
em taxa anual multiplicando-se a mesma por 12. Seja A = R$1000, n = 24 e
q = 5%. Determine a verdadeira taxa de juros.
Gabarito – Zero de Função
Exercí ci o 1:
2
Um exemplo é f(x) = (x - r ) , r ∈ R
A raiz x = r não pode ser determinada pelo Método da Bisseção porque f(x) • ∀ x ∈ R.
′ muda de sinal quando x se aproxima de r.
Temos também que f (x)
Exercí ci o 2:
Seja r a raiz de f(x). O método de Newton-Raphson pode não convergir se
[
−U é
“grande”.
Um exemplo: f(x) = arctg(x).
Para algum xc ∈ [1.39,1.40] , se x0 > xc , a seqüência {x n } diverge, xn − r
cada iteração.
Duas observações-extras:
1. Se x0 = xc , então o método produz o ciclo x1 = −xc , x 2 = xc , x3 = −xc,...
2. Se x0 < xc , a seqüência {x n } converge para r = 0.
Exercí ci o 3:
I = (2, 4).
(x) = x 2 − 6x + 12
f(x) = x 2 − 7x + 12
Supondo x0 = 2.1 , temos:
x1 = (2.1) 2 − 6(2.1) + 12 = 3.81
x 2 = 3.6561
cresce a
x 3 = 3.43046721
x4 = 3.185302019
x5 = 3.03433683 7
x6 = 3.001179018
x7 = 3.00000138 9
x8 = 2.999999997
x9 = 3.00000000 2
x10 = 2.999999998
x11 = 3
x12 = 3
.
.
.
xk = 3, k → ∞
Obs.: Se eu escolher x0 = 2, xk = 4, quando k → ∞.
Se eu escolher x0 = 4, xk = 4, quando k → ∞.
Mas, se eu escolher 2 < x0 < 4, xk = 3, quando k → ∞.
Para mostrar que a convergência é quadrática, temos que aplicar:
lim
n →∞
xn +1 − r
xn − r
2
= C, 0 ≤ C ≤ 1, quando n → ∞
Então:
lim
n →∞
x n +1 − 3
xn − 3
2
= lim
n →∞
((
n
) −3
xn − 3
2
= lim
x n 2 − 6x n + 12 − 3
n →∞
xn − 3
2
= lim
x n 2 − 6x n + 9
n →∞
xn − 3
2
= lim
n →∞
xn − 3
2
xn − 3
2
Portanto, a convergência é quadrática.
Exercí ci o 4:
Condição suficiente para convergência: × ′(r) < 1 ⇒ -1 < × ′(r) < 1
Aqui, sabemos que as raízes são: r1 = c e r2 = − c
Então, × ′(x) =
c
x
2
<1 ⇒ x
2
> c ⇒ x > c ⇒ x < − c ou x > c
Como r1 e r 2 não pertencem ao intervalo I = (- ∞, - c ) ∪ ( c , + ∞ ), logo não é possível
determinar a raiz quadrada de um número c ≥ 0 usando a função de iteração ×(x) =
Exercí ci o 5:
×1 (x) =
x2
− 2x + 4 ⇒ ×1' (x) = x − 2
2
Nas proximidad es da raiz (r ≈ 2), temos que ×1' (2) = 0
c
.
x
=1
× 2 (x) =
x2
− 2.5x + 5 ⇒ × 2 ' (x) = x − 2.5
2
Nas proximidad es da raiz (r ≈ 2) temos que × 2 ' (2) = 0.5
Como ×1' (2) < × 2' (2) , então ×1 (x) convergirá mais rapidamente para a raiz.
Veja o comportamento de ambas as funções:
Para ϕ1 (x)
Exercí ci o 6:
(a) f 1 (x) =
−
x −e x
−
x −e x =0 ⇒
−
−
−
x = e x ⇒ x = e 2x ⇒ ×1 (x) = e 2x
Graficamen te, percebemos que r ∈ (0,1).
Um bom intervalo para encontrar a raiz é I = (0.42, 0.44).
Usando x0 = 0.43 , temos:
x1 = 0.42316208 2 ⇒ Æ = 0.006837.. . > 0.001
x 2 = 0.42898893 ⇒ Æ = 0.005826.. . > 0.001
x 3 = 0.42401864 1 ⇒ Æ = 0.0049702. .. > 0.001
x4 = 0.42825465 ⇒ Æ = 0.00423600 9... > 0.001
x5 = 0.42464179 5 ⇒ Æ = 0.0036128. .. > 0.001
x6 = 0.42772124 6 ⇒ Æ = 0.00307945 ... > 0.001
x7 = 0.42509504 8 ⇒ Æ = 0.00262619 ... > 0.001
x8 = 0.42733368 9 ⇒ Æ = 0.00223864 ... > 0.001
Para ϕ 2 (x)
x9 = 0.42542467 3 ⇒ Æ = 0.00190901 5... > 0.001
x10 = 0.42705206 2 ⇒ Æ = 0.00162738 9... > 0.001
x11 = 0.42566436 2 ⇒ Æ = 0.00138769 9... > 0.001
x12 = 0.42684739 2 ⇒ Æ = 0.00118303 06... > 0.001
x13 = 0.42583863 9 ⇒ Æ = 0.00100875 208... > 0.001
x14 = 0.42669863 9 ⇒ Æ = 0.00086000 0166 < 0.001 ⇒ aqui está a aproxim ação!
(b) f 2 (x) = ln(x) − x + 2
ln(x) − x + 2 = 0 ⇒ x − 2 = ln(x) ⇒ x = e x −2 ⇒
2 (x)
= e x −2
Temos duas raízes : r1 ∈ (0, 0.5) e r2 ∈ (3, 3.5)
usando x0 = 0.43, temos :
x1 = 0.20804518 2 ⇒ Æ = 0.22195481 8 > 0.001
x 2 = 0.16663411 1 ⇒ Æ = 0.04141107 1 > 0.001
x 3 = 0.15987454 1 ⇒ Æ = 0.00675957 > 0.001
x4 = 0.15879750 2 ⇒ Æ = 0.00107703 9 > 0.001
x5 = 0.15862656 3 ⇒ Æ = 0.00017093 9 < 0.001 ⇒ aqui está a aproximaçã o!
(c)f 3 (x) = e x/2 − x 3
(
e x/2 − x 3 = 0 ⇒ e x/2 = x 3 ⇒ e x/2
Então, pelo gráfico, r ∈ (1, 2).
)
1/3
( )
= x3
1/3
⇒ e x/6 = x ⇒
3 (x)
= e x/6
x0 = 1.3 (uma a proximação inicial a rbitrária)
x1 = 1.24193005 6 ⇒ Æ = 0.05806994 4 > 0.001
x 2 = 1.22996823 4 ⇒ Æ = 0.01196182 2 > 0.001
x 3 = 1.22751856 6 ⇒ Æ = 0.0024496. .. > 0.001
x 4 = 1.2270175 ⇒ Æ = 0.00050106 ... < 0.001 ⇒ aqui está a aproxima ção!
(d)f4 (x) = sen(x) − x 2
41(x)
=
sen(x)
r1 ∈ (0, Ñ
x0 = 1.5
x1 = 0.99874670 7
x 2 = 0.91694774 5
x 3 = 0.89092581
x 4 = 0.88184699 9
x5 = 0.87858658 1
x6 = 0.87740386 8 ⇒ Æ = 0.00118271 3 > 0.001
x7 = 0.87697329 2 ⇒ Æ = 0.00043057 6 < 0.001 ⇒ uma das ra ízes
A outra raiz terá de ser encontrada em
(e ) f5 ( x ) =
42 (x)
= − sen(x)
x
− cos( x )
4
x
x
x 
− cos( x ) = 0 ⇒ cos( x ) = ⇒ x = arccos   ⇒
4
4
4
5(x)
x
= arccos  
4
Usando x0 = 1.5 temos :
x1 = 1.18639955 2 ⇒ Æ = 0.31360044 8 > 0.001
x 2 = 1.26966597 1 ⇒ Æ = 0.08326641 9 > 0.001
x 3 = 1.24779248 2 ⇒ Æ = 0.02187348 8 > 0.001
x 4 = 1.25355354 3 ⇒ Æ = 0.00576106 147 > 0.001
x5 = 1.25203725 5 ⇒ Æ = 0.00151628 804 > 0.001
x6 = 1.25243640 9 ⇒ Æ = 0.00039915 439 < 0.001 ⇒ uma aproxi mação para a raiz
Exercí ci o 7:
(i)
Método da Bisseção:
f 1 (x) =
x − e −x
r ∈ (0, 1);
x0 =
0 +1
= 0.5 ⇒ f 1 (0.5) = 0.10057612 1 > 0 ⇒ r ∈ (0, 0.5)
2
x1 =
0 + 0.5
= 0.25 ⇒ f 1 (0.25) = -0.2788007 83 < 0 ⇒ r ∈ (0.25, 0.5)
2
x2 =
0.25 + 0.5
= 0.375 ⇒ f 1 (0.375) = -0.0749168 43 < 0 ⇒ r ∈ (0.375, 0.5)
2
x3 =
0.375 + 0.5
= 0.4375 ⇒ f 1 (0.4375) = -0.8873924 7 < 0 ⇒ r ∈ (0.4375,0. 5)
2
x4 =
0.4375 + 0.5
= 0.46875 ⇒ f 1 (0.46875) = 0.05886918 7 > 0 ⇒ r ∈ (0.4375,0. 46875)
2
x5 =
0.4375 + 0.46875
= 0.453125 ⇒ f 1 (0.453125) = 0.03750692 7 > 0 ⇒ r ∈ (0.4375,0. 453125)
2
0.4375 + 0.453125
= 0.4453125
2
⇒ r ∈ (0.4375,0. 4453125)
x6 =
⇒ f 1 (0.4453125 ) = 0.02669334 1 > 0
0.4375 + 0.4453125
= 0.44140625
2
⇒ r ∈ (0.4375,0. 44140625)
x7 =
⇒ f 1 (0.4414062 5) = 0.02125273 1 > 0
0.4375 + 0.44140625
= 0.43945125
2
⇒ r ∈ (0.4375,0. 43945125)
x8 =
x9 =
⇒ f 1 (0.4394512 5) = 0.01852126 > 0
0.4375 + 0.43945125
= 0.43847562 5 ⇒ Æ = 0.43945125 -0.4384756 25 = 0.00097562 5 < 0.001
2
Portanto, a raiz apr oximada é x 9 = 0.43847562 5
(ii) Método da Falsa Posição:
Aqui, usamos média ponderada entre a e b com pesos |f(b)| e |f(a)|, respectivamente.
a f(b) + b f(a)
x =
f(b) + f(a)
=
af(b) − bf(a)
, visto que f(a) e f(b) têm sinais opostos.
f(b) − f(a)
r ∈ (0, 1) ⇒ f 1 (0) = −1 < 0 ; f 1 (1) = 0.63212055 8 > 0
0(0.632120 558) − 1( −1)
= 0.61269983 7 ⇒ f 1 (0.6126998 37) = 0.24086556 4 > 0
0.63212055 8 − ( −1)
⇒ r ∈ (0, 0.61269983 7)
x0 =
- 0.612699837(-1)
= 0.379921807 ⇒ f1(0.379921807) = - 0.067536909 < 0 ⇒
1.612699837
r ∈ (0.379921807, 0.612699837)
x1 =
0.379921807(0.240865564) − 0.612699837( −0.067536909)
= 0.430897755
0.240865564 − ( −0.067536909)
⇒ f1(0.430897755) = 0.00650268784 > 0 ⇒ r ∈ (0.379921807, 0.430897755)
x2 =
0.379921807(0.006502668784) − 0.430897755( −0.067536909)
= 0.426420694
0.006502668784 + 0.067536909
⇒ f1(0.426420694) = 0.000167316215 > 0 ⇒ r ∈ (0.379921807, 0.426420694)
x3 =
x4 = 0.426305782 ⇒ Æ = 0.000114911851 < 0.001 ⇒ aqui está uma aproximação!
Exercí ci o 8: Usar Método de Newton-Raphson para as letras (a), (b), (c), (d), (e) do Ex. 6.
Exercí ci o 9: Usar Método das Secantes para as letras (a), (b), (c), (d), (e) do Ex. 6.
Exercí ci o 10: Pontos extremos são pontos onde f’(x) = 0. Resolver essa equação por
Newton-Raphson para as letras (a), (b), (c), (d), (e) do Ex. 6.
Exercí ci o 11:
(i)
f1(x) = f 2 (x)
−
x − e x = ln(x) − x + 2
isolando x no membro esquerdo da equação, obtemos :
ln(x) =
x − e −x + x − 2 ⇒ x = e
x −e − x + x −2
w(x)
Pelo gráfico abaixo, temos duas raízes : r1 ∈ (0, 1) e r2 ∈ (1, 2).
Vamos resolver pelo Método de Newton-Raphson usando 4 casas decimais:
Aqui, já uso as equações :
h(x) = x − e − x − ln(x) + x − 2
h ′(x) =
1
+ e −x −
2 x
1
+1
x
Para aplicar a fórmula de Newton - Raphson :
xn +1 = xn −
h(x n )
h ′(xn )
Usando x0 = 0.07 temos :
x1 = 0.0759
x 2 = 0.0762
x 3 = 0.0762 ⇒ Aqui, está uma aproximaçã o!
f1(0.0762) = f 2 (0.0762) = −0.6506
Portanto, um dos pontos de interseção é P1 = (0.0762, - 0.6506)
Agora, para r2 ∈ (1, 2).
Usando x0 = 1.4, temos :
x1 = 1.3998
x 2 = 1.3998
f1(1.3998) = f 2 (1.3998) = 0.9365
Então, outro ponto de interseção é P2 = (1.3998, 0.9365)
(ii)
f 2 (x) = f 3 (x)
ln(x) - x + 2 = e x/2 − x 3 ⇒ e x/2 = ln(x) − x + 2 + x 3
h1 (x)
h 2 (x)
Pelo gráfico abaixo, temos apenas uma raiz r ∈ (0, 1) :
Vamos resolver pelo Método de Newton-Raphson usando 4 casas decimais:
Obs. :
f(x) = e x/2 − x 3 − ln(x) + x − 2
′ =
f (x)
1 x/2
1
− 3x 2 − + 1
e
2
x
Usando x 0 = 0.7, temos :
x1 = 0.8116
x 2 = 0.8022
x 3 = 0.8021
x 4 = 0.8021
f 2 (0.8021) = f 3 (0.8021) = 0.9774
O ponto de interseção é (0.8021, 0.9774)
f1 ∩ f 2 :
P1 = (0.0762, −0.6506)
P2 = (1.3998,0. 9365)
f 3 (0.0762) = 1.0384 ≠ −0.6506
f 3 (1.3998) = −0.7293 ≠ 0.9365
f 2 ∩ f 3 ⇒ P = (0.8021,0. 9774)
f 1 (0.8021) = 0.4472 ≠ 0.9774
Portanto, não existe ponto de interseção entre f1 , f 2 e f 3 simultanea mente.
Exercí ci o 12:
Substituin do os valores dados na equação, temos :
x 
arctg(x) = arctg(0) + (x - 0) f ′ 
2 
0
x 
arctg(x) = x f ′ 
2 
′
Sabendo que (arctg(x) ) =
1
, temos :
+
1 x2






1
1
4x
 ⇒ arctg(x) = x 

arctg(x) = x 
 4 + x 2 /4  ⇒ arctg(x) = 4 + x 2
1 +  x 2  


 4 
h1 (x)



h 2 (x)

(
)
Obs. : O exercício pede x > 0, então r ∈ (1, 2).
Vamos resolver por Método de Newton-Raphson com duas casas decimais:
f(x) = arctg(x) -
4x
x +4
2
5x 4 − 4x 2
x + 9x 4 + 24x 2 + 16
Usando x 0 = 1.4, temos :
′ =
f (x)
8
x 1 = 1.29
x 2 = 1.29
Então, x ≈ 1.29
Exercí ci o 13:
Definição: uma raiz ε da função f(x) é dita de multiplicidade p se 0
g(x) = (x - ε )-p f(x).
_J
ε )|”0H
Note que nessas condições: f( ε ) = f’( ε ) = f” ( ε ) = ... = f p-1 ( ε ) = 0.
Vamos mostrar agora um algoritmo, que tem convergência quadrática, mesmo quando
as raízes têm multiplicidade p > 1.
Considere o desenvolvimento de Taylor de f(x) na vizinhança da raiz ε . Então:
f ( x ) = f ( Æ ) + ( x − Æ ) f ′( Æ ) +
(x − Æ)2
(x − Æ) p
f ′′( Æ ) + ... +
f
2!
p!
p
(Æ) =
( x − Æ) p
f
p!
p
(  ), onde  ∈ ( x , Æ )
pois pela hipótese Æ é uma raiz de multiplicidade p. Derivando f(x), obtemos que:
f ′( x ) = p
( x − Æ ) p −1
f
p!
Definimos h(x) =
p
(Â ) =
( x − Æ ) p −1
f
( p − 1)!
p
(Â )
f (x)
.
f ′( x )
Então,
lim
x →Æ
h(x)
f(x)
= lim
= lim
′
− Æ x →Æ
x − Æ x →Æ f (x)(x
(x − Æ p f p (ÂÂ
p!
(x − Æ p −1 f p (ÂÂ − Æ
(p − 1)!
=
1
≠0
p
Da definição de multiplicidade conclui-se que h(x) tem uma raiz x = Æ simples ou de
multiplicidade 1, pois
lim h(x) =
x →Æ
1
lim (x − Æ = 0
p x →Æ
Dessa forma pode ser empregado qualquer método numérico para obtenção da raiz de
h(x), mantendo a ordem de convergência. Em particular para o Método de NewtonRaphson, temos:
x n +1 = x n −
h( xn )
,
h ′( x n )
n = 0,1,...
(1)
Por definição,
h( x ) =
f (x)
f ′( x )
⇒ h ′(x) = 1 -
′
f ′(x)f(x)
[f ′( x ) ]
2
= 1−
f ′′( x )
h( x ) .
f ′( x )
Assim temos o seguinte algoritmo para determinar a raiz simples da função h(x):

f ( xn )
h ( x n ) =
f ′( x n )


f ′′( x n )
h( xn ) ,
h ′( x n ) = 1 −
f ′( x n )


h( xn )
x n +1 = x n −

h ′( x n )
n = 0,1,...
(2)
Definição (Ordem de Convergência): Seja x n +1 = 3 ( x n ) , n = 0, 1, 2,... uma seqüência
convergente com lim x n = 0 e seja V uma vizinhança da raiz 0 tal que x n ∈ V para todo
n →∞
n. Então a iteração converge com ordem p > 1 em V, se × ∈ C p (V ) e
× (j) (Æ ) = 0 , ∀j = 1,2,...,(p - 1) e × (p) (Æ ) ≠ 0
Proposição: Considere a seguinte modificação do Método de Newton-Raphson
x n +1 = x n − p
f ( xn )
,
f ′( x n )
n = 0,1,...
Seja p a multiplicidade da raiz Æ de f(x). Prove que o método iterativo acima tem
convergência quadrática.
Prova: Usando a definição acima, basta mostrar que × ′′(Æ ) ≠ 0 , onde
×( x ) = x − p
f (x)
f ′( x )
Exercí ci o 14:
Seja x = Æ uma raiz de f(x), tal que f ′(Æ ) ≠ 0 e f ′′(Æ ) = 0 . Então do MNR tem-se que
x n +1 = x n −
f ( xn )
f ′( x n )
Subtraindo Æ em ambos os lados da igualdade e definindo o erro e n = x n − Æ tem-se
e n +1 = e n −
f ( xn )
f ′( x n )
(1)
Fazendo o desenvolvimento de Taylor de x na vizinhança de x n temos:
f ( x ) = f ( xn ) + ( x − xn ) f ′( xn ) +
( x − xn ) 2
( x − xn ) 3
f ′′( xn ) +
f ′′′( Ân ) , onde Ân ∈ (x , xn ) .
2!
3!
Tomando x = Æ em (2), obtemos
0 = f ( Æ ) = f ( x n ) − e n f ′( x n ) +
( en ) 2
(e ) 3
f ′′( x n ) − n
f ′′′( Â n )
2!
3!
(3)
′ n ) ≠ 0 , obtemos
Dividindo a igualdade por f (x
−
( e ) 2 f ′′( x n ) ( e n ) 3 f ′′′( Â n )
f ( xn )
−
= −e n + n
2!
3!
f ′( x n )
f ′( x n )
f ′( x n )
(4)
Substituindo em (1), obtemos que
e n +1 =
( e n ) 2 f ′′( x n ) ( e n ) 3 f ′′′( Â n )
−
2!
3!
f ′( x n )
f ′( x n )
Fazendo n → ∞ tem-se que lim
n →∞
lim
n →∞
e n +1
( en ) 3
= − lim
n →∞
f ′′( x n )
= 0 . Logo,
f ′( x n )
f ′′′( Â n )
f ′′′( Æ )
=−
=C ≠0
3! f ′( x n )
3! f ′( Æ )
Portanto a ordem de convergência é cúbica nesse caso.
(5)
(2)
Exercí ci o 15:
p(x) = x 4 − 2x 3 + 4x − 1.6
x 4 – 2x 3 = 1.6 – 4x
Gráfico de
Pela tabela abaixo:
x
p(x)
-2
22,4
-1
-2,6
0
-1,6
+1
1,4
+2
6,4
+3
37,4
+4
142,4
Temos duas raízes duplas: r1 ∈ ( −2,−1) e r2 ∈ ( 0, 1)
Vamos então aplicar o algoritmo de Briot-Ruffini com Newton-Raphson:
Para r1 ∈ ( −2,−1) , com uma aproximação inicial de
decimais, temos:
-1,50
-1,50
x1 = x0 −
-2
-3,50
-5,00
0
5,25
12,75
4
-3,88
-23,00 = p’(-1,50)
-1,6
4,22 = p(1,50)
4
-1,78
-15,64 = p’(-1,32)
-1,6
0,75 = p(-1,32)
4
-1,27
-13,87 = p’(-1,27)
-1,6
0,01= p(-1,27)§
p(x0 )
4,22
= −1,50 +
≈ −1,32
′
p (x0 )
23,00
-1,32
-1,32
x 2 = x1 −
1
1
1
x 0 = 1,50 e usando duas casas
1
1
1
-2
-3,32
-4,64
0
4,38
10,50
p(x1 )
0,75
= −1,32 +
≈ −1,27
p ′(x1 )
15,64
-1,27
-1,27
1
1
1
-2
-3,27
-4,54
0
4,15
9,92
Então, r1 ≈ 1,27
Para r2 ∈ ( 0, 1) , com uma aproximação inicial de x 0 = 0,50, vamos usar duas casas
decimais. Como já achamos uma das raízes ( r1 ≈ 1,27 ) então vamos usar apenas os
coeficientes do último q(x). Assim, temos:
1
1
1
0,50
0,50
-3,27
-2,77
-2,27
4,15
2,75
1,62 = p’(0,50)
-1,27
0,11 = p(0,50)
4,15
2,93
1,89 = p’(0,43)
-1,27
-0,01 = p(0,43)
4,15
2,90
1,85 = p’(0,44)
-1,27
0,01 = p(0,44)
p(x0 )
0,11
= 0,50 −
≈ 0,43
p′(x0 )
1,62
x1 = x0 −
1
1
1
0,43
0,43
-3,27
-2,84
-2,41
p(x1 )
0,01
= 0,43 +
≈ 0,44
p′(x1 )
1,89
x 2 = x1 −
0,44
0,44
1
1
1
-3,27
-2,83
-2,39
§
Então, r2 ≈ 0,44
Exercí ci o 16:
Dados do problema:
A = 1000 reais
N = 24 meses = 2 anos
q = 5% a.m = 60% a.a.
Substituindo esses dados na segunda equação do enunciado, que dá o valor de P,
temos:
60 
1
P = 1000  +
 = 1000 (0,5 + 0,6 ) = 1000 (1,1) = 1100 reais
2
100


Agora, substituindo os valores de A, P e n na equação de F(x), temos:
(
)
F(x) = (1000x - 1100)(1 + x) 2 + 1100 = 0 ⇒ F(x) = 10x 3 + 9x 2 − 12x = 0 ⇒ x 10x 2 + 9x − 12 = 0
Repare que x = 0 é uma das raízes da equação. Mas como se trata de taxa de juros,
essa raiz é descartada.
Vamos tentar resolver com o Algoritmo de Briot-Ruffini associado ao Método de NewtonRaphson.
Pela tabela abaixo:
x
F(x)
0
-12
1
7
2
46
...
...
Vemos mudança do sinal de F(x) para
[ ∈ .
Com uma aproximação inicial de x 0 = 0,50 temos:
0,50
0,50
10
10
10
9
14
19 = p’ (0,50)
-12
-5 = p(0,50)
x1 = x0 −
p(x0 )
5
= 0,50 +
≈ 0,76
′
p (x0 )
19
10
10
10
0,76
0,76
x 2 = x1 −
-12
0,62 = p(0,76)
p(x1 )
0,62
= 0,76 −
≈ 0,73
p ′(x1 )
24,20
0,73
0,73
x 3 = 0,73 +
Então, x
9
16,60
24,20 = p’ (0,76)
10
10
10
9
16,30
23,60 = p’ (0,73)
-12
-0,10 = p(0,73)
0,10
≈ 0,73
23,60
§
⇒ 73% a.a. ⇒
73
%a.m. ≈ 6,08 % a.m.
12