Solução

www.fisicaexe.com.br
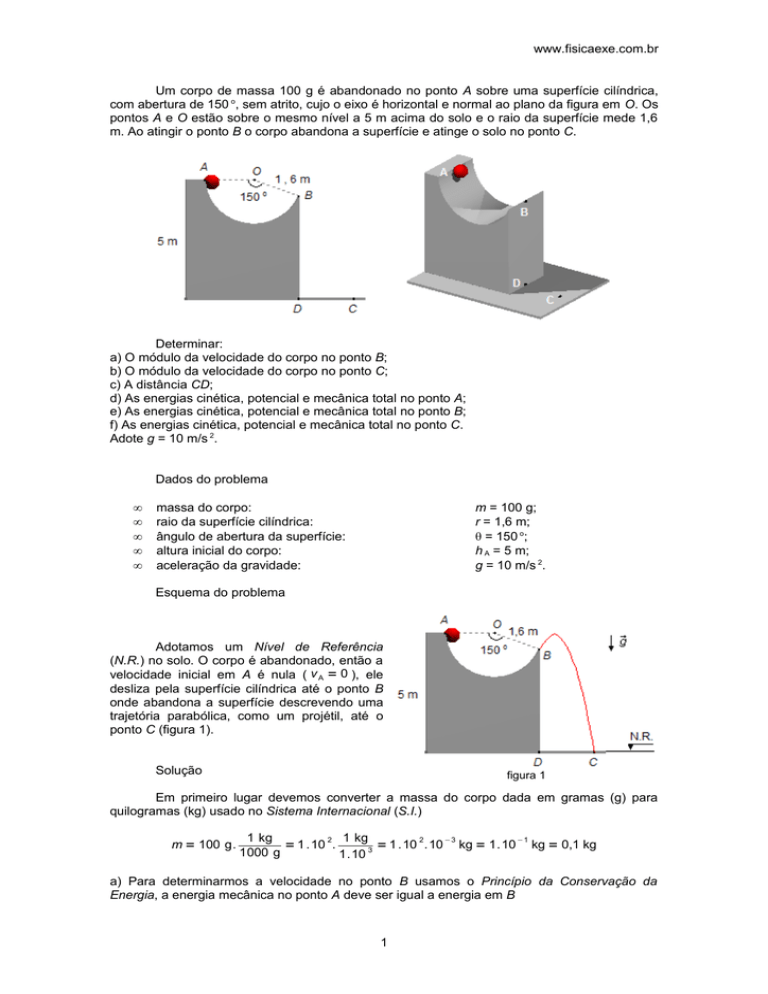
Um corpo de massa 100 g é abandonado no ponto A sobre uma superfície cilíndrica,
com abertura de 150 o, sem atrito, cujo o eixo é horizontal e normal ao plano da figura em O. Os
pontos A e O estão sobre o mesmo nível a 5 m acima do solo e o raio da superfície mede 1,6
m. Ao atingir o ponto B o corpo abandona a superfície e atinge o solo no ponto C.
Determinar:
a) O módulo da velocidade do corpo no ponto B;
b) O módulo da velocidade do corpo no ponto C;
c) A distância CD;
d) As energias cinética, potencial e mecânica total no ponto A;
e) As energias cinética, potencial e mecânica total no ponto B;
f) As energias cinética, potencial e mecânica total no ponto C.
Adote g = 10 m/s 2.
Dados do problema
•
•
•
•
•
massa do corpo:
raio da superfície cilíndrica:
ângulo de abertura da superfície:
altura inicial do corpo:
aceleração da gravidade:
m = 100 g;
r = 1,6 m;
θ = 150 o;
h A = 5 m;
g = 10 m/s 2.
Esquema do problema
Adotamos um Nível de Referência
(N.R.) no solo. O corpo é abandonado, então a
velocidade inicial em A é nula ( v A = 0 ), ele
desliza pela superfície cilíndrica até o ponto B
onde abandona a superfície descrevendo uma
trajetória parabólica, como um projétil, até o
ponto C (figura 1).
Solução
figura 1
Em primeiro lugar devemos converter a massa do corpo dada em gramas (g) para
quilogramas (kg) usado no Sistema Internacional (S.I.)
m = 100 g.
1 kg
2 1 kg
2
−3
−1
= 1 .10 .
kg = 1.10 kg = 0,1 kg
3 = 1 .10 . 10
1000 g
1.10
a) Para determinarmos a velocidade no ponto B usamos o Princípio da Conservação da
Energia, a energia mecânica no ponto A deve ser igual a energia em B
1
www.fisicaexe.com.br
À
B
EM= E M
E E ÀC = E BP E BC
2
2
mv A
mv B
m g h A
= m g h B
2
2
À
P
simplificando a massa m de ambos os lados da igualdade, temos
2
g h A
2
vA
vB
= g h B
2
2
(I)
Pela figura 2 vemos que
h A = hh B
portanto a altura do ponto B será de
h B = h A −h
(II)
O segmento O P é horizontal,
como o ângulo de abertura da superfície
 B será
cilíndrica é de 150 o, o ângulo P O
de 30 o (180 o – 150 o = 30 o).
Como o segmento O B é um raio
do cilindro e representa a hipotenusa do triângulo ΔPOB, temos
o
sen 30 =
o
da Trigonometria temos que sen 30 =
figura 2
cateto oposto
h
=
hipotenusa
r
1
, então
2
1
h
=
2 1,6
1,6
h=
2
h = 0,8 m
(III)
substituindo (III) em (II) e a altura do ponto A dada, a altura do ponto B será de
h B = 5−0,8
h B = 4,2 m
(IV)
substituindo (IV) em (I) e os dados do
problema, obtemos (figura 3)
2
2
vB
0
= 10 .4,2
2
2
v B2
500 = 42
2
2
vB
50− 42 =
2
2
v B = 2 .8
v B2 = 16
v B =  16
10.5
figura 3
v B = 4 m/s
2
www.fisicaexe.com.br
b) Para determinarmos a velocidade no ponto C usamos o Princípio da Conservação da
Energia, a energia mecânica no ponto A deve ser igual a energia em C.
A
C
EM =EM
A
E P E AC = E CP E CC
2
2
mv A
mv C
m g h A
= m g h C
2
2
simplificando a massa m de ambos os
lados da igualdade, temos
2
g h A
2
vA
vC
= g h C
2
2
(V)
substituindo os dados do problema e
sendo a altura do ponto C nula (h C = 0),
pois este ponto não tem altura em relação
ao Nível de Referência, temos
figura 4
2
2
vC
0
= 10. 0
2
2
2
vC
500 = 0
2
2
v
50 = C
2
2
v C = 2 .50
v 2C = 100
v C =  100
10. 5
v C = 10 m/s
c) Pela figura 5-B vemos que no movimento ao longo da direção x temos que para intervalos de
tempos iguais temos intervalos de espaços iguais (∆x1 = ∆x2 = ∆x3 = ∆x4 = Δx5). Na direção y
temos que durante a subida para intervalos de tempos iguais temos intervalos de espaços
menores, pois a esfera está sendo freada pela ação da gravidade (∆y1 > ∆y2) até que a
velocidade vy zera e então a gravidade começa a puxar o corpo de volta em direção ao solo
com velocidade acelerada, assim para intervalos de tempos iguais temos intervalos de espaços
cada vez maiores (∆y3 < ∆y4 < ∆y5)
figura 5
3
www.fisicaexe.com.br
A velocidade no ponto B pode ser decomposta ao longo dos eixos x e y. A velocidade
inicial vB, com que a esfera deixa a superfície, tem componentes nas direções x e y (figura 5-A)
o
v B x = v B cos 60
o
v B y = v B sen 60
o
Da Trigonometria temos que cos60 =
1
o
 3 e usando o valor de v
e sen 60 =
B
2
2
obtido no item (a), temos
1
2
v B x = 2 m/s
vB x = 4.
vB y = 4.
(VI)
3
v
2 B
v B y = 2  3 m/s
(VII)
Da decomposição do movimento vemos que na direção x não há aceleração agindo
sobre a esfera, então ela está em Movimento Uniforme (M.U.) e seu movimento é regido pela
equação
S x = S0 x v x t
como no movimento uniforme v x =v B x é constante podemos substituir vx pelo valor de (VI) e
S 0x =0
S x = 0 2 t
(VIII)
Sx = 2 t
Na direção y a esfera está sob a ação da aceleração da gravidade, portanto está em
queda livre que é regido pela equação
2
S y = S0 yv B y t−g
t
2
o sinal de negativo indica que a aceleração da gravidade está contra a orientação do
referencial, substituindo vBy pelo valor dado em (VII) e S 0 y = 4,2 m
2
t
2
2
S y = 4,22  3 t−5 t
S y = 4,22  3 t −10
(IX)
Quando o corpo atinge o solo no ponto C, que está no Nível de Referência, temos que
o espaço final ao longo do eixo y é nulo (S y = 0),
2
−5 t 2  3 t4,2 = 0
esta é uma Equação do 2.º Grau onde a incógnita é o valor de t desejado
2
2
Δ=b −4 a c =  2  3  −4 .−5. 4,2 = 4 . 320. 4,2 = 1284 = 96
t=
−b±  Δ −2  3 ±  96
−2 .1,73±9,80 −3,46±9,80
=
=
=
2a
−10
−10
2 . −5 
onde a raízes serão
4
www.fisicaexe.com.br
t 1=
−3,469,80
= −0,6
−10
e
t 1=
−3,46−9,80
= 1,3
−10
desprezando a primeira raiz que tem valor negativo (t 1 < 0), o tempo para a esfera atingir o
chão será t = 1,3 s . Como o intervalo de tempo para a esfera subir e descer é o mesmo que
ela leva para ir percorrer a distância CD ao longo do eixo x, substituindo este intervalo de
tempo na expressão (VIII), obtemos
S x = 2 . 1,3
S x = 2,6 m
d) Energia Cinética no ponto A
2
mv A
2
2
0,1 .0
A
EC=
2
A
EC =
A
EC=0 J
Energia Potencial no ponto A
A
E P = m g hA
E AP = 0,1 .10. 5
A
EP =5 J
Energia Mecânica Total no ponto A
A
A
A
E M = E CE P
E AM = 05
A
E M= 5 J
e) Energia Cinética no ponto B
2
m vB
2
0,1 . 4 2
B
EC=
2
0,1
.16
E BC =
2
1,6
B
EC =
2
B
EC=
B
E C = 0,8 J
Energia Potencial no ponto B
B
E P = m g hB
E = 0,1. 10. 4,2
B
P
B
E P = 4,2 J
5
www.fisicaexe.com.br
Energia Mecânica Total no ponto B
B
B
B
E M = E CE P
E BM = 0,84,2
B
E M= 5 J
f) Energia Cinética no ponto C
2
mv C
2
0,1 .10 2
C
EC =
2
0,1 . 100
C
E C=
2
10
C
EC=
2
C
E C=
C
E C= 5 J
Energia Potencial no ponto C
C
E P = m g hC
E CP = 0,1 .10. 0
C
EP=0 J
Energia Mecânica Total no ponto C
C
C
C
E M = E CE P
E CM = 50
C
E M= 5 J
Observação: nos pontos A, B e C as energias cinética e potencial têm valores diferentes
dependendo das velocidades e das alturas, respectivamente, mas a energia mecânica total é
sempre a mesma, uma vez que não há perdas e dissipações.
6