E Enten ndend do o T Teore ma d e Bay yes

Enten
E ndend
do o Teore
T
ma de Bay
yes
Vejamos
V
oa
assunto porr meio de um
m exemplo::
A cidade de
e Diabetelân
ndia tem 10.000 habita
antes, sendo
o 4.400 velh
hos, 3.300 jjovens, 2.300 criançass. Os
dados
d
mosttram que nesta
n
cidad
de está havvendo uma
a desertifica
ação urbanna em virtu
ude da falta
a de
empregos.
e
Foi
F realizad
da uma pessquisa pela Secretaria
a de Saúde
e onde se constatou
c
uuma grande
e incidência
a de
diabetes
d
na população
o. A pesquis
sa revelou que 132 ve
elhos são portadores
p
dda doença,, 33 jovenss são
portadores
p
e 46 criança
as são porta
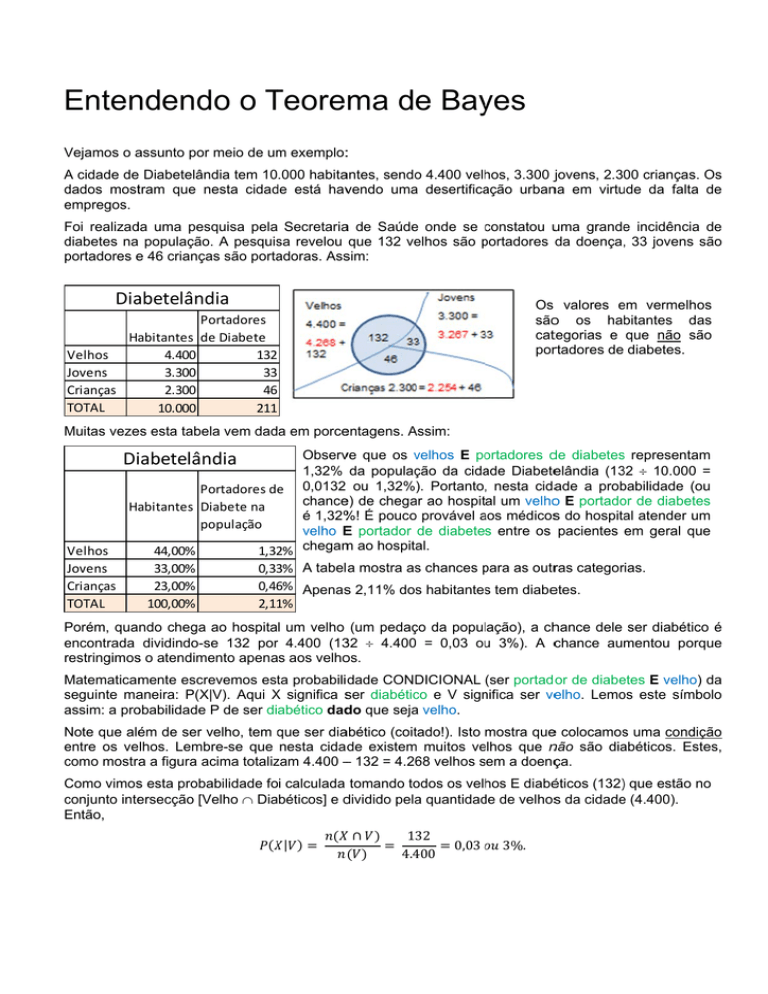
adoras. Asssim:
Diaabetelând
dia
Os valores em
e vermelh
hos
sãoo os habitantes das
d
cattegorias e que não são
s
porrtadores de diabetes.
Portadores Haabitantes de Diabete
V
Velhos
4.400
132
J
Jovens
3.300
33
Crianças
C
2.300
46
T
TOTAL
10.000
211
Muitas
M
veze
es esta tabe
ela vem dada em porce
entagens. Assim:
A
Observve que os velhos
v
E po
ortadores dde diabetes
s representa
am
1,32% da populaç
ção da cida
ade Diabeteelândia (13
32  10.000
0 =
babilidade (ou
(
Portadores de 0,0132 ou 1,32%). Portanto, nesta cidaade a prob
chance
e) de chega
ar ao hospital um velhoo E portado
or de diabettes
D
Diabete na é 1,32%
%! É pouco
o provável aos
a médicoss do hospita
al atender um
u
população
velho E portador de diabetes entre os pacientes em geral que
q
m ao hospita
al.
2% chegam
1,32
p
as outrras categorrias.
0,33
3% A tabel a mostra ass chances para
0,46
6% Apenass 2,11% doss habitantes
s tem diabeetes.
2,11
1%
Diiabetelân
ndia
Haabitantes
Velhos
V
J
Jovens
C
Crianças
T
TOTAL
44,00%
33,00%
23,00%
100,00%
Porém,
P
quando chega ao hospital um velho (um pedaç
ço da popullação), a chhance dele ser diabético é
dividindo-sse 132 porr 4.400 (13
encontrada
e
32  4.400 = 0,03 ou
u 3%). A cchance aumentou po
orque
re
estringimoss o atendimento apena
as aos velho
os.
Matematicam
M
mente escrrevemos estta probabili dade COND
DICIONAL (ser portadoor de diabe
etes E velho
o) da
seguinte
s
ma
aneira: P(X
X|V). Aqui X significa sser diabétic
co e V sign
nifica ser veelho. Lemo
os este sím
mbolo
assim:
a
a pro
obabilidade P de ser diabético dad
do que seja
a velho.
Note
N
que alé
ém de ser velho,
v
tem que
q ser dia
abético (coittado!). Isto mostra quee colocamos
s uma cond
dição
entre
e
os velhos. Lemb
bre-se que nesta cida de existem
m muitos ve
elhos que nnão são dia
abéticos. Esstes,
como
c
mostra
a a figura acima
a
totaliz
zam 4.400 – 132 = 4.26
68 velhos sem a doençça.
Como
C
vimoss esta proba
abilidade fo
oi calculada tomando to
odos os velhos E diabééticos (132)) que estão no
conjunto
c
inte
ersecção [V
Velho  Dia
abéticos] e d
dividido pela
a quantidad
de de velhoss da cidade
e (4.400).
Então,
E
|
∩
132
4.4
400
0,03
3%.
Lembrem-se que, os eventos ser velho e ser diabético são INDEPENDENTES. Isto significa que ser
velho não precisa ser diabético e ser diabético não precisa ser velho ou, em outras palavras, nem todo
velho é diabético e nem todo diabético é velho.
A expressão acima poderia ser calculada de outra maneira:
|
∩
∩
∩
1,32%
44%
0,03
3%.
Repetindo isto para as outras categorias podemos montar a seguinte tabela:
Diabetelândia
Habitantes
Velhos
Jovens
Crianças
TOTAL
44,00%
33,00%
23,00%
100,00%
Portadores de Diabetes na categoria P(X|Ai)
3,00%
1,00%
2,00%
2,11%
Cabe aqui a pergunta:
Qual a probabilidade de um velho ser diabético?
Resposta: 3%. Esta é a chance de aparecer em qualquer lugar da cidade um velho que é diabético.
Não precisa ter medo deles!!!! A chance é pequena e a doença não infecto-contagiosa!
Esta pergunta requer que encontremos P(X|V), certo?
Outra pergunta: Qual a probabilidade de um diabético ser velho?
É a mesma coisa que antes? 3%?
Posto de outra forma, chega ao hospital um diabético, qual a chance dele ser velho?
Agora queremos a probabilidade condicional P(V|X), ou seja, o contrário de antes. Imporemos agora
uma CONDIÇÃO entre todos os diabéticos – eles devem ser velhos. Observando a figura anterior,
temos que dividir nº de velhos diabéticos pelo total de diabéticos
|
∩
∩
∩
1,32%
2,11%
0,6256
62,56%.
Se atentarmos para os diabéticos da cidade, a chance dele ser velho é 62,56%. É, nesta cidade, entre
os diabéticos temos muitos velhos (ver figura acima).
Diabetelândia
Habitantes
Velhos
Jovens
Crianças
TOTAL
44,00%
33,00%
23,00%
100,00%
Fica bem claro que:
Portadores de A Categoria dos Diabetes na categoria Portadores de P(X|Ai)
Diabetes P(Ai|X)
3,00%
62,56%
1,00%
15,64%
2,00%
21,80%
2,11%
100,00%
Médicos, ao chegar um paciente
diabético, é muito grande (62,56%)
dele ser velho.
I.
II.
III.
P(X | Ai) ≠ P(Ai | X)
P(X  Ai) = P(A i X)
Pela definição de probabilidade condicional
|
Temos que: P(X  Ai) = P(X|Ai) P(Ai).
Dessa forma podemos fazer:
∩
|
∩
∩
∩
∩
⋯
∩
Ou, usando a definição de probabilidade condicional:
|
∩
P X|A P A
P X|A P A
P X|A P A
⋯
P X|A P A
∑
∩
P X|A P A
Este resultado recebe o nome de Teorema de Bayes.
USANDO TABELA
De acordo com o desenvolvimento anterior poderemos realizar os cálculos por meio de uma tabela.
Assim
Espaço Amostral
Participação da Partição do Partição no Espaço Espaço Amostral Amostral Ai
P(Ai)
P(X|Ai) conhecido
P(X  Ai) = P(X|Ai).P(Ai)
P(Ai|X)
A1
P(A1)
P(X|A1)
P(A1) * P(X|A1)
[P(A1) * P(X|A1)]/SOMA
A2
P(A2)
P(X|A2)
P(A2) * P(X|A2)
[P(A2) * P(X|A2)]/SOMA
A3
...
...
...
An
TOTAL
P(A3)
P(X|A3)
P(A3) * P(X|A3)
[P(A3) * P(X|A3)]/SOMA
P(An)
100,00%
P(X|An)
P(An) * P(X|An)
SOMA
[P(An) * P(X|An)]/SOMA
USANDO O EXCEL
Já que podemos fazer uma tabela, podemos também realizar tudo no Excel.
Abra uma pasta de trabalho e introduza os títulos conforme a figura abaixo:
Faça
F
100 pa
artições do espaço amostral (acho
o que fica o suficiente, não?). Com
m isso precisamos
selecionar
s
o intervalo A2:A101
A
e colocar
c
os tíítulos Ai.
Para
P
criarmo
os uma plan
nilha com re
ecursos ava
ançados do
o Excel, vam
mos definir uum nome ao intervalo de
células
c
onde
e existirem valores, deixando o re
esto das células em bra
anco, evitanndo assim colunas
c
com
m
ZEROS
Z
dessnecessários, pois não faremos cá
álculos naquelas linhas
s.
Para
P
se nom
mear um intervalo de células no E
Excel, procedemos sele
ecionando o intervalo de
d células
G2:G101,
G
de
epois na gu
uia Formata
ar, no grupo
o Nomes De
efinidos, esc
colhemos D
Definir Nome
e. Aparecerrá a
ja
anela:
Na
N caixa No
ome: ProbIn
nterseção
Na
N
ccaixa
e
a:
intrroduza
a
Refere-se
=DESLOC(P
=
PLAN1!$G$
$2;0;0;CONT.NÚM(Pla
an1!$G$2:$G
G$101;1)). Dê OK.
seguinte
fórm
mula:
Selecione
S
o intervalo G2:G101 e escolha a cor bran
nca para a fonte. Issoo para não poluir a no
ossa
disto para evitarmos as
planilha
p
com
m dados e precisamos
p
a referencias circularees do Excel ao introdu
uzir a
fu
unção SOM
MA na célula
a D101..
Vamos
V
ente
ender o que fizemos. Primeiro, porr que usar a função DE
ESLOC?
Esta função embutida do Excel retorna uma referência a um intervalo que possui um número específico
de linhas e colunas com base em um referência especificada (no nosso caso se houver número e a
existência ou não de números é identificado com a função CONT.NÚM que falaremos abaixo). A sintaxe
da função DESLOC é: =DESLOC(ref;Lins;cols;altura;largura). Os argumentos em negrito são
obrigatórios e os outros são opcionais.
A função CONT.NÚM calcula o nº de células em um intervalo que contém números. Sua sintaxe é:
CONT.NÚM(valor1;valor2;....). Novamente os argumentos em negrito são obrigatórios. Aqui usamos
valor2 = 1, para não retornar zero quando não encontrar número e com isso causando um erro de
altura na função DESLOC.
Dessa forma a função DESLOC nomeará o intervalo na coluna G que tiver números e com isso não
serão introduzidos zeros quando a célula estiver em branco na coluna D que apresenta a fórmula
SOMA(DADOS) na célula D101.
Voltemos à célula D2 e introduzimos a fórmula: =SE(B2=””;””;B2*C2) e na célula E2, introduzimos:
=SE(D2=””;””;D2/$D$102).
A planilha ficou pronta. Agora é só salvar e guardar com carinho para quando precisar.
DIAGRAMA DE ÁRVORE
O diagrama de árvore ajuda a montar o problema e fazer as contas.
Voltemos à cidade Diabetelândia e vemos que lembremos que a população foi dividida em 3 categorias
de habitantes (velhos, jovens e crianças). Algumas das pessoas de cada categoria eram portadoras de
diabetes.
Então, estabelecendo que X é portador e
não é portador, temos
0,0132
0,0211
X 0,44 x 0,03 = 0,0132 ou 1,32%
0,6256
62,56%
0,1564
15,64%
3%
V
97%
44%
X 0,33 x 0,01 = 0,0033 ou 0,33%
0,0033
0,0211
1%
33%
J
99%
23%
X 0,23 x 0,02 = 0,0046 ou 0,46%
2%
0,0046
0,0211
0,2180
21,80%
______________
C
0,0211 ou 2,11%
98%
EXERCÍCIOS RESOLVIDOS
1. Uma urna A contém 3 fichas vermelhas e 2 azuis, e uma urna B contém 2 vermelhas e 8 azuis. Jogase uma moeda “honesta”. Se a moeda der cara, extrai-se uma ficha da urna A; se der coroa, extraise uma ficha da urna B. Uma ficha vermelha é extraída.
Qual a probabilidade de ter saído cara no lançamento da moeda?
Solução
A
B
3V
2V
2A
8A
Queremos encontrar a probabilidade de sair cara
dado a bola ser vermelha, isto é P(Ca|V)
P(A) = P(Ca) = (1/2)
P(V|A) = (3/5) = 60% = P(V|Ca)
P(B) = P(Co) = (1/2)
P(V|B) = (2/10)= 40% = P(V|Co)
Pelo Teorema de Bayes, temos
|
∩
P X|A P A
P X|A P A
P X|A P A
⋯
P X|A P A
∑
∩
P X|A P A
|
∩
∩
3 20
10
0 8
P V|A P A
P V|A P A
P V|B
V P B
60
0
80
3
4
0,75
5
3 1
5 2
3 1 2 1
5 2 10 2
3
10
3
0
10
2
20
6
3
10
20
2
75%
Temos, p
portanto, 75% de probabilid
dade de qu
ue a bola vermelha seja extr
raída da urna
u
A por te
er obtido cara no lançamento
l
o da moeda
a.
Na plani
ilha Excel
l, preench
ha apenas a área az
zul:
Faça o e
exercício usando a árvore.
2.
2 A caixa A tem 9 carttas numerad
das de 1 a 9
9. A caixa B tem 5 carttas numeraddas de 1 a 5. Uma caixa é
escolhida ao acaso e uma carta é retirada. Se
e o número é par , qual a probabiliddade de que a carta sortteada
tenha vind
do de A?
Solução
A
1234
5678
9
B
1234
5
Queremos
s encontr
rar a prob
babilidad
de da car
rta vir
da urna A dado que
q
o seu número é par, is
sto é
P(A|par) .
P(A) = (
(1/2)
) = (4/9)=
= 44,44%
P(par|A)
P(B) = (
(1/2)
P(par|B)
) = (2/5)=
= 40%
Pelo Teo
orema de Bayes,
B
tem
mos
|
|
∩
P X|A P A
∩
4
18
P X|A P A
P X|A P A
40 36
4
180
∩
de
P X|A P A
P par|A P A
P par|A P A
P par|B P B
4 180
76
18
1
Temos, portanto,
, 52,63%
extraída
a da urna A.
⋯
40
7
76
10
19
proba
abilidade
0,5263
de
Na plani
ilha Excel
l, preench
ha apenas a área az
zul:
∑
∩
P X|A P A
4 1
9 2
4 1 2 1
9 2 5 2
4
18
4
18
2
10
5
52,63%
que a
carta
de
núme
ero
par
s
seja
3.
3 Num colégio, 4% doss homens e 1% das mu
ulheres têm mais de 1,75 m de altu ra. 60% dos
s estudantess são
mulheres. Um estuda
ante é escollhido ao aca
aso e tem mais
m
de 1,75
5 m. Qual a probabilida
ade de que seja
homem?
Solução
er mais de
e 1,75 m d
de altura.
.
A = evento te
P(M) = 6
60%
P
P(A|M)
= 1%
1
P(H) = 4
40%
P
P(A|H)
= 4%
4
Quer
remos P(H|
|A)
Pelo Teo
orema de Bayes,
B
tem
mos
∩
|
∩
|
P X|A P A
∩
0,016
6
0,022
2
8
11
P X|A P A
P X|A P A
⋯
P A |H P H
P A|H P H
P A|M P M
0,7273
P X|A P A
∑
0,04 0,440
0,0
04 0,40 0,,01 0,60
∩
P X|A P A
0,016
006
0,016 0,0
72 ,73%
Temos, p
portanto, 72,73% de
d probabi
ilidade de
e que o es
studante c
com mais de 1,75 m de
escolhido ao acaso
altura e
o seja ho
omem. Embo
ora o colégio tenh
ha mais mulher
m
do que
homem, h
há mais ho
omens com altura su
uperior a 1,75 m do
o que mulh
heres.
Na plani
ilha Excel
l, preench
ha apenas a área az
zul:
4.
4 Uma caixxa tem 3 mo
oedas: uma não viciada
a, outra com
m 2 caras e uma terceeira viciada, de modo que a
probabilidade de ocorrrer cara nes
sta moeda é 1/5. Uma moeda
m
é selecionada aoo acaso na caixa. Saiu cara.
obabilidade de
d que a 3ª moeda
m
tenha
a sido a selec
cionada?
Qual a pro
Solução
A = primeira moeda,
m
B = segunda moeda,
C = terceira moeda
P(A) = 1
1/3
P
P(Ca|A)
= 50% ou 1/
/2
P(B) = 1
1/3
P
P(Ca|B)
= 100% ou 1
P(C) = 1
1/3
P
P(Ca|C)
= 20% ou 1/
/5
Querem
mos P(C|Ca
a)
Pelo Teo
orema de Bayes,
B
tem
mos
∩
|
∩
|
P X|A P A
P X|A P A
P X|A P A
∩
P Ca|A P A
0,20 1/3
1
1
1
1
0,,20
3
3
3
0,5
50
⋯
P X|A P A
∑
P Ca|C
C
P C
P Ca|B
C
P B
P Ca|C P C
0,20
0,20
2
0,5
50 1 0,2
20 1,70 17
∩
P X|A P A
0,117
76
11,76%
%
Temos, p
portanto, 11,76% de
d probabi
ilidade de
e que a face cara seja apre
esentada pela
p
3ª moeda
a quando esta
e
for escolhida
e
ao acaso.
.
Na plani
ilha Excel
l, preench
ha apenas a área az
zul:
5.
5 A probabilidade de um
m indivíduo de classe A comprar um
m carro de 3/4,
3 da B é dde 1/5 e da C é de 1/20
0. As
probabilidades se os indivíduos co
omprarem um
m carro da marca
m
x são 1/10, 3/5 e 33/10, dado qu
ue sejam de A, B
e C, respectivamente. Certa loja vendeu um carro da ma
arca x. Qual a probabili dade de que
e i indivíduo
o que
comprou sseja da classse B?
Solução
A = classe A,
,
B = classe B,
C = classe C
P(A) = 3
3/4
P
P(car|A)
= 1/10
P(B) = 1
1/5
P
P(car|B)
= 3/5
P(C) = 1
1/20
P
P(car|C)
= 3/10
Qu
ueremos P(
(B|car)
Pelo Teo
orema de Bayes,
B
tem
mos
∩
|
|
∩
P X|A P A
P X|A P A
P X|A P A
∩
⋯
P X|A P A
∑
∩
P X|A P A
P car|B P B
P car|B P B
P car|A P A
3 1
3
5
5
25
3
3
3
1 3 3 1 3 1
40 25 200
10 4 5 5 10 20
0,5714 57,14%
P car|C P C
3
3 200
2
25
15 24 3 25 42
200
4
7
Temos, portanto, 57,14% de proba
abilidade de que o carro
indivídu
uo da clas
sse B.
foi comp
prado por
r um
Na plani
ilha Excel
l, preench
ha apenas a área az
zul:
6.
6 Um certo programa pode
p
ser usado com um
ma entre duas sub-rotinas A e B, ddependendo do problem
ma. A
experiência tem mosttrado que a sub-rotina A é usada 40
0% das veze
es e B é usaada 60% da
as vezes. Se
eAé
usada, exxiste 75% de
e chance de que o progrrama chegue a um resu
ultado dentroo do limite de tempo. Se
eBé
usada, a cchance é de
e 50%. Se o programa fo
oi realizado dentro
d
do lim
mite de tempoo. Se B é us
sada, a chan
nce é
de 50%. S
Se o programa foi realiz
zado dentro do limite de
e tempo, qua
al a probabillidade de qu
ue a sub-rotina A
tenha sido
o a escolhida
a?
Solução
40%
P(A) = 4
P
P(resultad
do|A) = 75
5%
P(B) = 6
60%
P
P(resultad
do|B) = 50
0%
Quere
emos P(A|r
resultado).
Pelo Teo
orema de Bayes,
B
tem
mos
|
∩
P X|A P A
P X|A P A
P X|A P A
∩
|
0,75 0,40
0,75
5 0,40 0,5
50 0,60
∩
0,30
0
0,30 0,30
⋯
P X|A P A
∑
∩
P X|A P A
P resuultado|A P A
P ressultado|A P A
P resultado|B P B
0,30 1
0,5000 50,00%
0,60 2
Temos, p
portanto, 50,00% de
e probabi lidade de
e que o re
esultado f
foi atingi
ido dentro
o do
limite u
usando a sub-rotina
s
a A.
Na plani
ilha Excel
l, preench
ha apenas a área az
zul:
7. A urna X contém 2 bolas azuis, 2 brancas e 1 cinza, e a urna Y contém 2 bolas azuis, 1 branca e 1 cinza.
Retira-se uma bola de cada urna. Calcule a probabilidade de saírem 2 bolas brancas sabendo-se que são
bolas de mesma cor?
Solução
X
Y
2 A
2
A
2 B
1
B
1 C
1
C
Após retirar uma bola de cada urna queremos
saber P(B  B|mesma cor).
A cor da bola que sai da segunda urna não é influenciada pela cor da bola que saiu
da primeira urna, isto é os eventos são independentes.
P(mesma cor) = P(BB) + P(AA) + P(C  C)= P(B).P(B) + P(A).P(A) +
P(C).P(C) = (2/5)(1/4) + (2/5)(2/4) + (1/5)(1/4) = (2/20)+(4/20)+(1/20) =
(7/20) = 0,35 ou 35%
Agora
P BB|mesmacor
∩
8. Uma companhia de transporte urbano tem três linhas numa cidade, de forma que 45% dos ônibus cobrem o
serviço da linha 1, 25% cobre a linha 2 e 30% cobre o serviço da linha 3. Sabe-se que a probabilidade de que,
diariamente, um ônibus quebre é de 2%,3% e 1%, respectivamente, para cada linha.
a. Calcular a probabilidade de que, em um dia, um ônibus quebre.
b. Calcular a probabilidade de que, em um dia, um ônibus não quebre.
c. De que linha de transporte é mais provável que um ônibus quebre?
Solução
A1 = Cobre o serviço da linha 1
A2 = Cobre o serviço da linha 2
A3 = Cobre o serviço da linha 3
B1 = Quebra
B2 = Não quebra
P(A1) = 45% = 0,45
P(A2) = 25% = 0,25
P(A3) = 30% = 0,3
P(B1|A1) = 2% = 0,02
P(B1|A2) = 3% = 0,03
P(B1|A3) = 1% = 0,01
P(B2|A1) = 1 - P(B1|A1) = 1 - 0,02 = 0,98
P(B2|A2) = 1 - P(B1|A2) = 1 - 0,03 = 0,97
P(B2|A3) = 1 - P(B1|A3) = 1 - 0,01 = 0,99
a. A probabilidade de que, em um dia, um ônibus quebre, representada por P(B1), é
encontrada pela probabilidade total:
P(B1) = P(A1  B1) + P(A2  B1) + P(A3  B1)
P(B1) = P(A1).P(B1|A1) + P(A2).P( B1|A2) + P(A
P 3).P(B1|A
| 3)
P(B1) = 0,45.0
0,02 + 0,2
25.0,03 + 0,30.0,01
1 = 0,0195
5 ou 1,95%
%
b. A pro
obabilidad
de de que,
, em um di
ia, um ôni
ibus não quebre,
q
re
epresentada por P(B2),
é enc
contrada pela
p
proba
abilidade total:
P(B2) = P(A1  B2) + P(A2  B2) + P(A3  B2)
P(B2) = P(A1).P(B2|A1) + P(A2).P( B2|A2) + P(A
P 3).P(B2|A
| 3)
P(B2) = 0,45.0
0,98 + 0,2
25.0,97 + 0,30.0,99
9 = 0,9805
5 ou 98,05
5%
Ou ta
ambém, sab
bendo-se que
q
P(B2) = 1 – P(B
B1) = 1 – 0,0195 = 0,9805 ou
u 98,05%.
c. Para encontrar
rmos a lin
nha de tra
ansporte que
q
seja a mais pro
ovável de um ônibus
quebr
s. Assim
rar, aplic
camos o te
eorema de Bayes a cada
c
uma das
d
linhas
∩
|
1 | 1
0,4615
0
46
6,15%
P X|A P A
1∩ 1
1∩ 1
1
1
2 | 1
2
3 | 1
3
∩
1
1
1
∩
1
P X|A P A
P X|A P A
∩
1| 1 2
1
1
1
∩
1
3
P
1
1| 2
⋯
P X|A P A
1| 1 1
1| 2 2
P
2
1
P
1| 3
P
3
1
1| 3 33
∩
P X|A P A
∑
,
,
,
0,03 0,25
0,0195
0,3846
38,46%
0,01 0,30
0,0195
0,1538
15,38%
Temo
os, portan
nto, a linha A1 ap
presentand
do a maior
r chance (maior pr
robabilida
ade)
de u
um ônibus quebrar.
Na p
planilha Excel,
E
pre
eencha ape
enas a áre
ea azul:
9.
9 Uma emp
presa dedicada à comerc
cialização de
e televisores
s está consid
derando com
mercializar um
m novo televvisor.
No passad
do 90% dos televisores que
q comercia
alizou tiveram êxito e 10
0% não. Sabee-se que a probabilidade
p
e que
.recebera um relatório
o favorável de
e pesquisa fo
oi de 85% e 35%, respec
ctivamente.
e a probabilid
dade de que os televisore
es exitosos recebem um relatório dessfavorável de
e pesquisa
a. Calcule
b. Calcule
e a probabilid
dade de que os televisore
es não exitos
sos recebam
m um relatórioo desfavoráv
vel de pesquiisa.
c. Calcule a probabilid
dade de que um televisorr receba um relatório favo
orável de pessquisa. P(B1) = 0,8
d. Calcule
e a probabilid
dade de que um televisorr receba um relatório des
sfavorável dee pesquisa. P(B
P 2) = 0,2
e. Qual é a probabilida
ade de que o equipamen
nto do televis
sor tenha êxitto no mercaddo? P(A1|B1) = 0,9563
Solução
levisores exitosos
A1 = Tel
P(A1) = 90%
A2 = Tel
levisores não exito
osos
P(A2) = 10%
B1 = Rel
latório fa
avorável de
d pesquis
sa
B2 = Rel
latório de
esfavoráve
el de pesq
quisa
P(B1|A1) = 85%
P(B1|A2) = 35%
a.
b.
c.
d.
e.
P(B2|
|A1) = 15
5%
P(B2|
|A2) = 65
5%
P(B1) = P(A1).P(B1|A1) + P(A2).
.P(B1|A2)= 0,90x0,
,85 + 0,1
10x0,35 = 0,8
P(B2) = P(A1).P(B2|A1) + P(A2).
.P(B2|A2)= 0,90x0,
,15 + 0,1
10x0,65 = 0,2
Aqui queremos
s P(A1|B1) e será encontra
ado pelo teorema de Bayes
s
P 1| 1 P 1
1∩ 1
1∩ 1
1 | 1
P 1 | 1 P 1
P 1 | 2 P 2
1
1
0,76550
0,85 0,90
0,7650
0,9563 95,63%
0,85 0,90 0,35
0,8
5 0,10 0,7
7650 0,0350
No Excel:
10. A probabilidade de qu
ue uma pess
soa tenha um
ma determina
ada doença é 0,02.
agnóstico mé
édico disponííveis para de
eterminar se uma pessoaa tem realme
ente a doença
a. Se
Existem provas de dia
a doença estiver realmente prese
ente, a proba
abilidade de
e que a prov
va de diagnóóstico indique a presençça da
doença é de 0,95.
a. Qual é a probabilidade de se
e ter a doen
nça, se a prova
p
de diagnóstico inddica a prese
ença da messma?
Calcular à mão e no
n Excel.
b. Qual é a probabiliidade de não
o ter a doençça, se a prov
va de diagnó
óstico não inndica a prese
ença da messma?
Calcular à mão e no
n Excel.
Solução
P(A
P 1) = Pro
obabilidade de que uma pess oa tenha determina
ada doença
a = 0,02 ou
o 2%.
obabilidade de que uma pess oa não te
P(A
P 2) = Pro
enha deter
rminada do
oença = 0,98 = 98%.
P(B
P 1|A1) = Probabili
idade de que
q
o dia
agnóstico indique a presença
a da doenç
ça dado qu
ue a
pessoa
p
est
teja doent
te = 0,95 ou 95%.
P(B
P 1|A2) = Probabili
idade de que
q
o dia
agnóstico indique a presença
a da doenç
ça dado qu
ue a
pessoa
p
não
o esteja doente
d
= 0,05
0
ou 5%
%.
P(B
P 2|A1) = 1 – P(B1|A1) = 1 – 0,95 = 0 ,05 ou 5%
P(B
P 2|A2) = 1 – P(B1|A2) = 1 – 0,05 = 0 ,95 ou 95%
a. O qu
ue querem
mos é a probabili
idade de uma pessoa ter a doença
a dado qu
ue a
prov
va de dia
agnóstico
o indica a presen
nça da mes
sma = P(A
A1|B1).
P
Para isso
o usamos o teorema
a de Baye
es:
∩
|
1 | 1
0,2794
0
27,94%
P X|A P A
P X|A P A
P X|A P A
1∩ 1
1∩ 1
1
1| 1 1
1| 1 1
⋯
P X|A P A
1
1| 2 2
,
,
,
,
,
∑
,
∩
P X|A P A
,
,
b. Agor
ra o que queremos é a pr
robabilid
dade de uma
u
pesso
oa NÃO ter a doe
ença
dado
o que o diagnósti
d
ico NÃO i
indica a presença
a da mesm
ma = P(A
A2|B2). Ai
inda
P(B2) = 1 – P(B1) = 1 – 0,068
80 = 0,93
320 ou 93
3,20%
2 | 2
2
∩
2
2
2
∩
2
2
P
2| 2
P
0,9320
2
0,95 0,988
0,9320
0,9989
99,98%
No Exce
el:
11. Uma fábrrica de sacolas tem 3 má
áquinas inde pendentes que
q produzem
m o mesmo ttipo de saco
olas. A máquina 1
produz 15
5% das sacollas, com 1% delas com d
defeito. A má
áquina 2 prod
duz 45% dass sacolas, co
om 3% delass com
defeito. A máquina 3 produz
p
40% das
d sacolas,, com 2% de
elas com defe
eito.
a.
elecionarmoss uma sacola
a aleatoriame
ente, qual é a probabilida
ade de que eela seja defe
eituosa?
Se se
b.
a uma sacola, se a sacola não tem ddefeito?
De qu
ual máquina é mais provável que saia
Solução
P(A1) = Probabili
idade da sacola
s
ser
r produzid
da pela má
áquina 1 = 15%
P(A2) = Probabili
idade da sacola
s
ser
r produzid
da pela má
áquina 2 = 45%
P(A3) = Probabili
idade da sacola
s
ser
r produzid
da pela má
áquina 3 = 40%
P(B1|A1) = Probabilidade da
d sacola com defei
ito vir da
a máquina 1 = 1%
P(B1|A2) = Probabilidade da
d sacola com defei
ito vir da
a máquina 2 = 3%
P(B1|A3) = Probabilidade da sacola com defeito vir da máquina 3 = 2%
P(B2|A1) = Probabilidade da sacola boa, vir da máquina 1 = 1 - P(B1|A1) = 99%
P(B2|A2) = Probabilidade da sacola boa, vir da máquina 2 = 1 - P(B1|A2) = 97%
P(B2|A3) = Probabilidade da sacola boa, vir da máquina 3 = 1 - P(B1|A3) = 98%
a. Queremos a probabilidade de que a sacola seja defeituosa.
P(B1) ?
P(B1) = P(B1  A1) + P(B1  A2) + P(B1  A3)
P(B1) = P(A1). P(B1|A1) + P(A2). P(B1|A2)+ P(A3). P(B1|A3)
P(B1) = 0,15x0,01 + 0,45x0,03 + 0,40x0,02 = 0,0015 + 0,0135 + 0,0080 = 0,0230 ou
2,30%
b. Para sabermos qual a máquina mais provável de produzir uma sacola sem defeito
(boa), basta aplicarmos o Teorema de Bayes a todas as máquinas e elegermos a
maior probabilidade:
P(B2) = 1 – P(B1) = 1 – 0,0230 = 0,9770
1 | 2
1
2 | 2
2
∩
2
2
2
∩
∩
1
2
2
2
2
2
∩
2
P
P
P
0,9770
2| 2 P
0,9770
1
2
0,99 0,15
0,9770
0,97 0,45
0,9770
0,1520
15,20%
0,4468
44,68%
0,98 0,40
P 3
0,4012 40,12%
0,9770
0,9770
2
2
A máquina mais provável de produzir uma sacola boa é a máquina 2 com uma
probabilidade 44,68%.
3 | 2
3
∩
2
2
∩
3
P
2| 1
2| 3
12. O primeiro ano de bacharelado no curso de Administração de uma Universidade é integrado por 35 estudantes
que se especializarão em Recursos Humanos (RH), 47 em Agronegócios e 40 em Finanças e 38 em
Administração Geral. Sabe-se que a probabilidade que um estudante seja reprovado é de 5%, 4%, 3% e 4%,
respectivamente. Qual a especialidade é mais provável que seja o estudante, se sabemos que ele ficou
reprovado?
Solução
P(A1)=Probabilidade do estudante cursar a especialidade RH=(35/160)=0,2188 ou 21,88%
P(A2)=Probabilidade do estudante cursar a especialidade Agronegócios=(47/160)=0,2938
ou 29,38%
P(A3)=Probabilidade do estudante cursar a especialidade Finanças=(40/160)=0,2500 ou
25,00%
P(A4)=Probabilidade
do
estudante
Geral=(38/160)=0,2375 ou 23,75%
cursar
a
especialidade
Administração
P(B1|A1) = Probabilidade dos alunos de RH serem reprovados = 5% = 0,05.
P(B1|A2) = Probabilidade dos alunos de Agronegócios serem reprovados = 4% =
0,04
P(B1|A3) = Probabilidade dos alunos de Finanças serem reprovados = 3% = 0,03.
P(B1|A4) = Probabilidade dos alunos de Adm. Geral serem reprovados = 4% = 0,04
A especialidade mais provável de vir um aluno reprovado é encontrada
verificando-se o maior dos P(Ai|B1) (probabilidade da especialidade dado que o
aluno é reprovado).
P(B1) = P(B1  A1) + P(B1  A2) + P(B1  A3) + (B1  A4)
P(B1) = P(A1). P(B1|A1) + P(A2). P(B1|A2)+ P(A3). P(B1|A3)+ P(A4). P(B1|A4)
P(B1) = 0,2188
8x0,05 + 0,2938x0,0
0
04 + 0,2500x0,03 + 0,2375x0
0,04 = 0,0
0109 + 0,0
0118
+ 0,0
0075 + 0,0
0095 = 0,0
0397 ou 3,
,97%
∩
1 | 1
1
2 |1
2
3 | 1
3
4 | 1
4
1
1
∩
1
∩
1
1
A especialid
dade
Agronegócios.
.
∩
2
1
1
1
1
∩
1
1
∩
1
∩
3
1
1
1
1
∩
4
1
mai
is
prová
ável
P
1| 1
1
P
1| 2
2
P
0,0397
0
P
0,0397
0
P
1| 3
P
0,0397
0
3
0,05 0,21188
0,03977
0,2938x0,004
0,0397
0,2500x00,03
0,2960
0
27,56
6%
29,60%
%
0,188
89
18,89%
%
P 4
0,2375x00,04
0,239
93
0,0397
0
0,03977
de vir um aluno reprovad
do
23,93%
%
P
1| 4
0,275
56
0,03977
é
a
do
,
X 0,44 x 0,03 = 0,0132 ou 1,32%
,
0,6256
62,56%
0,1564
15,64%
3%
V
97%
44%
X 0,33 x 0,01 = 0,0033 ou 0,33%
,
,
1%
33%
J
99%
23%
X 0,23 x 0,02 = 0,0046 ou 0,46%
2%
C
______________
0,0211 ou 2,11%
98%
Jovens
Velhos
3.300 =
4.400 =
4.268 +
132
132
33
3.267 + 33
46
Crianças 2.300 = 2.254 + 46
,
,
0,2180
21,80%