n x x = 1 - professor.tulio.uss

Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
1. REVISÃO DE ESTATÍSTICA
Aplicando a regra dos 5%.
1.1.
ESTATÍSTICA DESCRITIVA
5% de 51 = 2,55
A estatística descritiva é a etapa inicial da análise
utilizada para descrever e resumir os dados. A
disponibilidade de uma grande quantidade de dados e
de métodos computacionais muito eficientes revigorou
esta área da estatística.
Em determinada pesquisa, verificou-se a idade que as
pessoas conseguiam ter seu próprio carro. Foram
perguntadas 100 pessoas e obteve-se a seguinte tabela
de dados:
53
32
49
58
62
R = 56,1
Logo para o cálculo das classes
k = 56,1/10 = 5,61 classes  6 classes
1.1.1. Agrupamento de Dados
44
Então expande-se o intervalo de 12,45 até 67,55.
Com isso tem-se uma nova amplitude corrigida.
40
21
27
Então 56,1/6 = 9,35  intervalo de classe igual 9
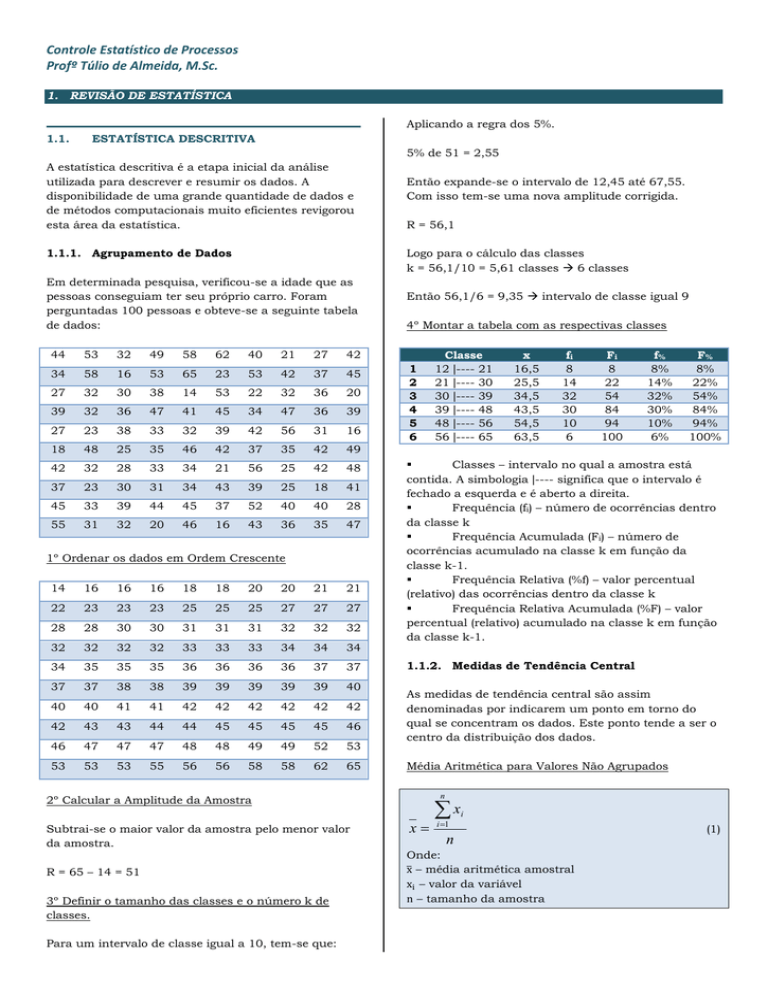
4º Montar a tabela com as respectivas classes
42
34
58
16
53
65
23
53
42
37
45
27
32
30
38
14
53
22
32
36
20
39
32
36
47
41
45
34
47
36
39
27
23
38
33
32
39
42
56
31
16
18
48
25
35
46
42
37
35
42
49
42
32
28
33
34
21
56
25
42
48
37
23
30
31
34
43
39
25
18
41
45
33
39
44
45
37
52
40
40
28
55
31
32
20
46
16
43
36
35
47
1º Ordenar os dados em Ordem Crescente
14
16
16
16
18
18
20
20
21
21
22
23
23
23
25
25
25
27
27
27
28
28
30
30
31
31
31
32
32
32
32
32
32
32
33
33
33
34
34
34
34
35
35
35
36
36
36
36
37
37
37
37
38
38
39
39
39
39
39
40
40
40
41
41
42
42
42
42
42
42
42
43
43
44
44
45
45
45
45
46
46
47
47
47
48
48
49
49
52
53
53
53
53
55
56
56
58
58
62
65
1
2
3
4
5
6
R = 65 – 14 = 51
3º Definir o tamanho das classes e o número k de
classes.
Para um intervalo de classe igual a 10, tem-se que:
x
16,5
25,5
34,5
43,5
54,5
63,5
fi
8
14
32
30
10
6
Fi
8
22
54
84
94
100
f%
8%
14%
32%
30%
10%
6%
F%
8%
22%
54%
84%
94%
100%

Classes – intervalo no qual a amostra está
contida. A simbologia |---- significa que o intervalo é
fechado a esquerda e é aberto a direita.

Frequência (fi) – número de ocorrências dentro
da classe k

Frequência Acumulada (Fi) – número de
ocorrências acumulado na classe k em função da
classe k-1.

Frequência Relativa (%f) – valor percentual
(relativo) das ocorrências dentro da classe k

Frequência Relativa Acumulada (%F) – valor
percentual (relativo) acumulado na classe k em função
da classe k-1.
1.1.2. Medidas de Tendência Central
As medidas de tendência central são assim
denominadas por indicarem um ponto em torno do
qual se concentram os dados. Este ponto tende a ser o
centro da distribuição dos dados.
Média Aritmética para Valores Não Agrupados
n
2º Calcular a Amplitude da Amostra
Subtrai-se o maior valor da amostra pelo menor valor
da amostra.
Classe
12 |---- 21
21 |---- 30
30 |---- 39
39 |---- 48
48 |---- 56
56 |---- 65
x
x
i 1
i
n
Onde:
x̅ – média aritmética amostral
xi – valor da variável
n – tamanho da amostra
(1)
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Quando é possível realizar um censo da população dos
dados em análise usa-se de forma similar a equação
para médias populacionais:
N

x
i 1
i
(2)
N
Moda
A moda de um conjunto de dados é o valor que ocorre
com maior frequência. Quando dois valores ocorrem
com a mesma frequência máxima, cada um deles é
uma moda e o conjunto se diz bimodal. Quando tal
situação ocorre com três ou mais valores o conjunto é
multimodal. Há casos onde não há moda. Tal medida
de tendência central é representada por Mo.
Para o exemplo abordado, o conjunto é bimodal, há
frequência idêntica (7) de dois valores, o 32 e o 42.
Onde:
μ – média aritmética populacional
xi – valor da variável
N – tamanho da população
Para o exemplo dado é:
x
A mediana de um conjunto de valores é o valor do meio
deste conjunto quando os valores estão dispostos em
ordem crescente (ou decrescente). É representada
geralmente por Med.
Para o exemplo abordado, a mediana é o valor 37.
3714
 x  37,14
100
1.1.3. Medidas de Dispersão
Média Aritmética para Dados Agrupados
Desvio ou Amplitude
n
x
x f
i i
i 1
(3)
n
Onde:
x̅ – média aritmética amostral
xi – média do intervalo de classe
fi – frequência do intervalo de classe
n – tamanho da amostra
R  máx( xi )  mín( xi )
Para o exemplo dado é:
x
Uma medida de dispersão muito útil e muito simples
de se calcular, a amplitude de variação ou
variabilidade trabalha com valores absolutos. É muito
usual quando a escala do desvio padrão é muito
pequena.
Variância
3824
 x  38,24
100
Também é utilizada para análises de variabilidade.
Matematicamente, é o quadrado do desvio padrão.
Observação: A forma como ocorre o agrupamento pode
interferir no valor da média aritmética.
Outra medida de tendência central que é muito
importante, a diferença é que esta faz uso de pesos,
para diferenciar a importância dos valores. Tais valores
normalmente são atribuídos a critérios.
n
xp 
i 1
n
i
i
w
i 1
i 1
i
x

2
(6)
n 1
Desvio Padrão
Dentre as medidas de dispersão, destaca-se o desvio
padrão que pode ser assim como a média aritmética,
amostral ou populacional.
Para determinar o padrão de variação de um grupo de
dados, a princípio, considerando uma amostra de
dados tem-se a equação a seguir:
i
Onde:
wi – peso de cada critério.
Mediana
(4)
 x
n
s2 
Média Ponderada
w x
(5)
n
s
 (x  x )
2
i
i 1
n 1
Onde:
s – desvio padrão amostral
x̅ – média amostral
x𝑖 – valor da variável
(7)
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
n – tamanho da amostra
E para a população tem-se outra equação similar:
N

 (  x )
2
i
i 1
N
(8)
Onde:
σ – desvio padrão populacional
μ– média populacional
xi – valor da variável
N – tamanho da população
1.1.4. Gráficos Típicos
Gráfico é um recurso visual da Estatística utilizado
para representar um fenômeno. Sua utilização em
larga escala nos meios de comunicação social, técnica
e científica, devem-se tanto à sua capacidade de refletir
padrões gerais e particulares do conjunto de dados em
observação, como à facilidade de interpretação e a
eficiência com que resume informações dos mesmos.
Embora os gráficos forneçam menor grau de detalhes
que as tabelas, estes apresentam um ganho na
compreensão global dos dados, permitindo que se
aperceba imediatamente da sua forma geral sem deixar
de evidenciar alguns aspectos particulares que sejam
de interesse do pesquisador.
Uma representação gráfica coloca em evidência as
tendências, as ocorrências ocasionais, os valores
mínimos e máximos e também as ordens de grandezas
dos fenômenos que estão sendo observados.
Histograma
É um gráfico de colunas justapostas que representa
uma distribuição de frequência para dados contínuos
ou uma variável discreta quando esta apresentar
muitos valores distintos.
No eixo horizontal são dispostos os limites das classes
segundo as quais os dados foram agrupados enquanto
que o eixo vertical corresponde às frequências
absolutas ou relativas das mesmas.
É um gráfico que permite descrever dados
quantitativos por meio da frequência acumulada.
A ogiva é um gráfico de linha que une os pontos cujas
abscissas são os limites superiores das classes, e,
ordenadas suas respectivas frequências acumuladas.
Convém observa-se que o ponto inicial desse gráfico é
o limite inferior do primeiro intervalo, com frequência
acumulada zero, pois não existe qualquer valor inferior
a ele.
Quando os dados contidos em cada classe são
distribuídos uniformemente, pode-se estimar, a partir
da ogiva, o número de elementos pertencentes a
qualquer uma das classes que compõe a distribuição
de frequência dos dados e a quantidade ou
porcentagem de elementos que estão abaixo de certo
valor pertencente ao conjunto de dados.
1.2.
PROBABILIDADE E ESTATÍSTICA
A teoria de probabilidades nos permite descrever os
fenômenos aleatórios, ou seja, aqueles em que está
presente a incerteza.
A palavra probabilidade deriva do Latim probare
(provar ou testar). Informalmente, provável é uma das
muitas palavras utilizadas para eventos incertos ou
conhecidos, sendo também substituída por algumas
palavras como “sorte”, “risco”, “azar”, “incerteza”,
“duvidoso”, dependendo do contexto.
1.2.1. Probabilidade de Eventos Independentes
A probabilidade de ocorrência do evento A ou do evento
B pode ser dada pela seguinte equação.
P(A  B)  P(A)  P(B)
A
Exemplo:
Ogiva
B
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Jogando-se aleatoriamente 1 dado, qual a
probabilidade de se obter um número par?
Como o dado possui 6 faces, tem-se 6 possibilidades
(espaço amostral). Logo as probabilidades individuais
se distribuem da seguinte forma:
P(X=1) = 1/6
P(X=2) = 1/6
P(X=3) = 1/6
P(X=4) = 1/6
P(X=5) = 1/6
P(X=6) = 1/6
Os números 2,4 e 6 são pares, porém só será possível
obter um deles. Desta forma será 2 OU 4 OU 6.
P( x  par) 
1 1 1 3 1
   
6 6 6 6 2
Ou seja, 50% de chance.
Exemplo:
Em uma prova foram propostas duas questões.
Nenhum dos participantes zerou a prova e obteve-se a
seguinte estatística:
80% das pessoas acertaram a 1ª questão.
40% das pessoas acertaram a 2ª questão.
Qual a porcentagem de pessoas que acertaram apenas
uma das duas questões?
P(X=1)= 0,80
P(X=2)= 0,40
P(X=1e2) = 0,80.0,40 = 0,32
Então:
P(x  apenas1)  0,80  0,40  0,32  0,88
1.2.2. Probabilidade de Eventos Dependentes
A probabilidade de ocorrência do evento A e do evento
B pode ser dada pela seguinte equação.
P(A  B)  P(A).P(B)
A
P(AB)  P(A)  P(B)  P(A).P(B)
B
Exemplo:
Jogando-se aleatoriamente 2 dados, qual a
probabilidade de se obter dois números 6?
Como o dado possui 6 faces, tem-se 6 possibilidades
(espaço amostral). Logo as probabilidades individuais
se distribuem da seguinte forma:
P(X=1) = 1/6
P(X=2) = 1/6
P(X=3) = 1/6
P(X=4) = 1/6
P(X=5) = 1/6
P(X=6) = 1/6
Logo, deseja-se calcular a probabilidade de se obter 6
no primeiro dado e 6 no segundo dado.
1 1 1
P( x  6e6)  . 
6 6 36
Ou seja, 2,8% de chance.
1.2.3. Probabilidade de Eventos Mutuamente
Exclusivos
A probabilidade de ocorrência do evento A ou do evento
B, mas não ambos, pode ser dada pela seguinte
equação.
1.2.4. Probabilidade Condicional
A probabilidade de ocorrência de A, dada a
probabilidade de ocorrência de B.
A probabilidade condicional também pode ser dada
pela função. Se ..., então ....
P(AlB) 
P(A  B)
P(B)
Pode ser lido da seguinte maneira:
Probabilidade de A dado B, ou seja, calcula-se a
probabilidade de A condicionada a probabilidade de B
(conhecida).
Observação: Tal conceito faz uso do Teorema de Bayes.
Exemplo:
Em uma urna há um total de 10 bolas, sendo 3
amarelas, 4 azuis e 3 verdes. É retirada uma bola
dessa urna, ao acaso, e verifica-se que ela é verde.
Qual a probabilidade de se retirar uma bola azul
sabendo que a bola verde retirada inicialmente não foi
reposta?
O primeiro passo é identificar os eventos em questão.
Evento A: sair uma bola azul
Evento B: sair uma bola verde
Resolver o exercício consiste em determinar a
probabilidade de se retirar uma bola azul da urna
sabendo que já foi retirada uma bola verde. Observe
que a ocorrência do evento A está condicionada à
ocorrência do evento B. Esse é o caso mais simples de
problemas envolvendo probabilidade condicional, não
sendo necessária a aplicação da fórmula. Veja:
Após a retirada da bola verde, restaram na urna 9 das
10 bolas. Dessas 9 bolas, 4 são azuis. Assim, temos
que:
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
P(AIB) 
1.3.
Probabilidade de X ser igual a três.
P(X=3)=?
4
9
Variáveis Quantitativas Contínuas
VARIÁVEIS ALEATÓRIAS
São compostas de dados numéricos contidos em
intervalos.
1.3.1. Tipos de Variáveis
Alguns conjuntos de dados consistem em números,
enquanto outros não são números. Utiliza-se a
nomenclatura de dados (ou variáveis) qualitativos ou
quantitativos.
Probabilidade de X estar contido entre 20 e 25.
P(X|20<X<25)=?
Esquema Gráfico
Conjuntos Numéricos
V = [0;100]
Variáveis Discretas  Inteiros (ℤ)
Variáveis Contínuas  Reais (ℝ)
Discretas
Quantitativas
Contínuas
Variáveis
Nominais
Qualitativas
Ordinais
1.3.2. Variáveis Qualitativas
São dados categóricos ou atribuídos (não numéricos)
que não podem ser expressos em números.
Variáveis Qualitativas Nominais
Não há sentido de ordenação, separando os dados por
categorias.
Exemplo: raça de cavalo, sexo, estado civil, cor dos
olhos etc.
Variáveis Qualitativas Ordinais
Há sentido de ordenação, separando os dados por
classes.
Exemplo: faixa de idade, nível de instrução, classe
social.
Observação: Há uma espécie de “hierarquia” entre as
classes.
1.3.3. Variáveis Quantitativas
Variáveis Quantitativas Discretas
São compostas por dados numéricos, valores pontuais
absolutos que podem ser contados.
Os dados discretos resultam de um conjunto finito de
valores possíveis, ou de um conjunto enumerável
desses valores (ou seja, o número de valores possível é
0, ou 1, ou 2 etc.)
V = { 1,2,3,4,5,6,7,8,9,10}
1.4.
DISTRIBUIÇÕES DISCRETAS DE
PROBABILIDADE
1.4.1. Distribuição Binomial
Considera-se experimentos que satisfaçam as
seguintes condições:
a.
O experimento deve ser repetido, nas mesmas
condições, um número finito de vezes (n).
b.
As provas repetidas devem ser independentes,
isto é, o resultado de uma não deve afetar os
resultados das sucessivas.
c.
Em cada prova deve aparecer um dos dois
possíveis resultados: sucesso e insucesso.
d.
No decorrer do experimento, a probabilidade p
do sucesso e a probabilidade q (q = 1-p) do insucesso
manter‐se‐ão constantes.
A distribuição binomial é usada em problemas do tipo:
determinar a probabilidade de se obterem k sucessos
em n tentativas.
O experimento “obtenção de caras em cinco
lançamentos sucessivos e independentes de uma
moeda” satisfaz essas condições.
Sabe-se que, quando da realização de um experimento
qualquer em uma única tentativa, se a probabilidade
de realização de um evento (sucesso) é p, a
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
probabilidade de não‐realização desse mesmo evento
(insucesso) é 1 – p = q.
Suponhamos, agora, que realizemos a mesma prova n
vezes sucessivas e independentes. A probabilidade de
que um evento se realize k vezes nas provas é dada
pela função:
n
f ( x )  P(X  k )   .p k .q n k
k
Onde:
P (X=k) – é a probabilidade de que o evento se realize k
vezes em n provas;
p – é a probabilidade de que o evento se realize em
uma só prova – sucesso;
q – é a probabilidade de que o evento não se realize no
decurso dessa prova – insucesso;
n
 
k
- é o coeficiente binomial de n sobre k, igual a
n!
(n  k )!.k!
Média
  n.p
Variância
 2  n.p.(1  p)
Desvio Padrão
  n.p.(1  p)
1.4.2. Distribuição Hipergeométrica
Um experimento hipergeométrico é um experimento
estatístico que tem as seguintes propriedades:

Uma amostra de tamanho n é selecionada
aleatoriamente sem reposição de uma população de N
itens.

Na população, k itens podem ser classificados
como sucessos e N – k itens podem ser classificados
como fracassos.
sucesso seja constante em cada tentativa. Com o
experimento acima, a probabilidade de um sucesso
muda em cada tentativa. No início, a probabilidade
de selecionar uma bolinha vermelha é 5/10. Se
você selecionar uma bolinha vermelha na primeira
tentativa, a probabilidade de selecionar uma
bolinha vermelha na segunda tentativa é 4/9. E se
você selecionar uma bolinha verde na primeira
tentativa, a probabilidade de selecionar uma bolinha
vermelha na segunda tentativa é 5/9.
Note ainda que se você selecionou as bolinhas com
reposição, a probabilidade de sucesso não mudaria.
Ela seria 5/10 em cada tentativa. Então, este seria um
experimento binomial.
Notação
A seguinte notação é útil, quando falamos a respeito
da probabilidade hipergeométrica e distribuições
hipergeométricas:

N: O número de itens na população.

k: O número de itens na população que são
classificados como sucessos.

n: O número de itens na amostra.

X: O número de itens na amostra que são
classificados como sucessos.

C kx : O número de combinações de k coisas,
tomando x coisas de cada vez.

h(x;N,n,k): Probabilidade hipergeométrica ‐ a
probabilidade que um experimento hipergeométrico
de n‐tentativas resulte em exatamente x sucessos,
quando população consistir de N itens, k dos quais são
classificados como sucessos.
Função de Probabilidade
Uma variável aleatória hipergeométrica X é o número
de sucessos que resulta de um experimento
hipergeométrico. A distribuição de probabilidades de
uma variável aleatória hipergeométrica é chamada
função distribuição hipergeométrica.
C kx .C nNxk
h (X  x; N, n, k ) 
C nN
Fazendo
p
Exemplo
Esperança
Considere o seguinte experimento estatístico. Você tem
uma urna de 10 bolinhas de gude – 5 vermelhas e 5
verdes.
Você seleciona aleatoriamente 2 bolinhas de gude sem
reposição e conta o número de bolinhas vermelhas
que você selecionou. Este seria um experimento
hipergeométrico.
Note que não será um experimento binomial. Um
experimento binomial exige que a probabilidade de
E(X)  n.p
k
Nk
e q
N
N
Variância e Desvio Padrão
Var (X)  n.p.q.
Var (X)   2
( N  n)
( N  1)
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
1.4.3. Distribuição de Poisson
A distribuição de Poisson é empregada em
experimentos, nos quais não se está interessado no
número de sucessos obtidos em n tentativas, como
ocorre no caso da distribuição Binomial, mas sim no
número de sucessos ocorridos durante um intervalo
contínuo, que pode ser um intervalo de tempo, espaço,
etc. Como por exemplo:

O número de suicídios ocorridos em uma
cidade durante um ano;

O número de acidentes automobilísticos
ocorridos numa rodovia em um mês;

Número de chegadas a um caixa automático de
um banco durante um período de 15 minutos

A probabilidade de um carro chegar a um
posto de gasolina em quaisquer dois períodos de tempo
de mesmo tamanho.

A chegada ou não chegada de um carro em
qualquer período de tempo independentemente da
chegada ou não chegada de outro carro em qualquer
outro período.

Defeitos por unidade (m2, m, etc.) por peça
fabricada

Erros tipográficos por página, em um material
impresso

Carros que passam por um cruzamento por
minuto, durante certa hora do dia.

Usuários de computador ligados à Internet
Note que nos exemplos acima, não há como
determinar‐se a probabilidade de ocorrência de um
sucesso, mas sim a frequência média de sua
ocorrência, como, por exemplo, dois suicídios por ano,
a qual será que denominada λ.
É, então, uma distribuição de probabilidade discreta
que se aplica a ocorrência de eventos ao longo de
intervalos especificados. A variável aleatória é o
número de ocorrência do evento no intervalo. Os
intervalos podem ser de tempo, distância, área, volume
ou alguma unidade similar.
Uma variável aleatória X admite distribuição de
Poisson se:
distribuição de Poisson têm os valores de X de 0; 1; 2;
_ _ _ , sem qualquer limite superior.
Observação: O parâmetro λ é usualmente referido como
taxa de ocorrência.
Propriedades do experimento de Poisson:
a.
A probabilidade de uma ocorrência é a mesma
para quaisquer dois intervalos
b.
A ocorrência ou não ocorrência em qualquer
intervalo é independente da ocorrência ou não‐
ocorrência em qualquer intervalo.
1.5.
DISTRIBUIÇÕES CONTÍNUAS DE
PROBABILIDADE
1.5.1. Função Densidade de Probabilidade
A Função Densidade de Probabilidade (fdp),
apresenta de forma matemática (função) o
comportamento probabilístico de um determinado
evento através de seus dados amostrais. Tal função é
vinculada diretamente a uma Distribuição de
Probabilidade.
A função densidade possui as seguintes propriedades:

f (x)  0


 f (x)dx  1



P(a  x  b)  b  f ( x )dx
a
onde a integral de a até b define a área sob a curva f(x).
1.5.2. Função de Distribuição Acumulada
A distribuição acumulada de probabilidade é a
integral da função densidade, conforme segue na
equação.
b

X = {0, 1, 2, ...} (não tem limites);
F(a  x  b)   f ( x )dx

e   .k
P( X  k ) 
k!
Os valores de F(X) são tais quais que:
, k = 0, 1, 2, ...; é a
probabilidade de k ocorrências em um intervalo

E(X) =  =  ;

Var(X) =  2 =  .
Uma distribuição de Poisson difere de uma
distribuição binomial nestes aspectos fundamentais:
1. A distribuição binomial é afetada pelo tamanho da
amostra n e pela probabilidade p, enquanto que a
distribuição de Poisson é afetada apenas pela média _;
2. Na distribuição binomial, os valores possíveis da
variável aleatória X são 0; 1; 2; _ _ _ ; n, mas a
a
0  F(x)  1
1.5.3. Distribuição Uniforme
A distribuição uniforme é a mais simples distribuição
contínua, entretanto uma das mais importantes e
utilizadas dentro da teoria de probabilidade. A
distribuição uniforme tem uma importante
característica a qual a probabilidade de acontecer um
fenômeno de mesmo comprimento é a mesma.
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Definição
Uma variável aleatória X tem distribuição Uniforme no
intervalo [a,b] se sua função densidade de
probabilidade for dada por:
 1

f (x)   b  a

0
, se a ≤ x ≤ b
O gráfico que segue apresenta uma função densidade
de probabilidade (fdp) para a=0 e b=1.
A função densidade de probabilidade é:
f (x) 
1
e
2 2
1  x  
 

2  
2
Simplificando para que se faça uso da tabela z, tem-se
que:
x 
z

  
Logo:
A função de distribuição acumulada (fda) se dá pelo
cálculo do área do gráfico.
f (z) 
1
2 2
e

z2
2
A função de distribuição acumulada é definida por:
F( x )   f ( x )dx
F(x)
Obtendo assim:
F(z)   f (z)dz
F(z)  
1
2 2
e

z2
2
dz
Os valores de z são tabelados e podem ser encontrados
na tabela z reduzida ou na completa.
1.5.4. Distribuição Normal
1.5.5. Distribuição t de Student
Dentre as distribuições contínuas, é a mais conhecida
devido as suas diversas aplicações e fazer uso de
parâmetros de tendência central e dispersão como a
média aritmética e o desvio padrão.
Uma variável aleatória contínua X tem distribuição t
de Student com ν graus de liberdade se sua função
densidade de probabilidade é dada por
 1 
 (  1) 
2  2 
2


x
 .1 

f (x)  


 
.

2
 
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Onde:
ν – (nu) - graus de liberdade (amostral), equivale a n-1.
Γ (ν/2) - (gama) – valor obtido para o ν/2 na tabela
Gama.
A fdp é dada por:
f (x)  e x
Graficamente pode ser vista da seguinte forma:
Mas os tamanhos das amostras são algumas vezes
pequenos, e frequentemente não conhecemos o desvio
padrão da população. Quando um destes problemas
ocorrerem, os estatísticos contam com a distribuição
da estatística t (também conhecida como t‐score), cujos
valores são dados por:
x 
t
s
n
x
F( x )   e x dx
0
Fazendo mudança de variáveis:
u  x
du
du
   dx 
dx

onde:
t – variável t
𝑥̅ – média amostral
μ - média populacional
s - desvio padrão amostral
n – tamanho da amostra
Substituindo, tem-se que:
A distribuição t de Student tem grande importância
para a inferência de parâmetros da população e para a
estatística de pequenas amostras.
F(x)  1  e x
 x
F( x ) 
 e
u
0
 
du
 F( x )   e u

x
0
 e   x  [ e 0 ]
Desta forma, obtém-se a seguinte fda:
A distribuição exponencial não faz uso de tabelas!
Observação: A distribuição t de Student, faz uso da
tabela t, que é usual para amostras inferiores a 30
unidades.
1.5.6. Distribuição Exponencial
Esta é uma distribuição que se caracteriza por ter uma
função de taxa de falha constante. A distribuição
exponencial é a única com esta propriedade. Ela é
considerada uma das mais simples em termos
matemáticos. Esta distribuição tem sido usada
extensivamente como um modelo para o tempo de vida
de certos produtos e materiais. Ela descreve
adequadamente o tempo de vida de óleos isolantes e
dielétricos, entre outros.
1.6.
ESTATÍSTICA INFERENCIAL
É o estudo de técnicas que possibilitam a extrapolação,
a um grande conjunto de dados, das informações e
conclusões obtidas a partir da amostra.
1.6.1. Amostragem
Uma área importante em muitas aplicações
Estatísticas é a da Tecnologia de Amostragem.
Exemplos de Aplicação:

Pesquisa de mercado,

Pesquisa de opinião,

Avaliação do processo de produção,

Praticamente em todo experimento.
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Amostragem Aleatória
Cada elemento da
população tem a mesma
chance de ser escolhido.
Observação: Viável para amostras inferiores ou iguais a
30 unidades.
Exemplo:
A seguinte amostra: 9, 8, 12, 7, 9, 6, 11, 6, 10, 9 foi
extraída de uma população normal. Construir o
intervalo de confiança de 95%, para μ.
Amostragem Estratificada
Classificar a população
em, ao menos dois
estratos e extrair uma
amostra de cada um.
Calculando-se a média:
x  8,7
Calculando-se o desvio padrão:
s  2,0
Da tabela, obtém-se que:
Amostragem Sistemática
t  / 2  2,262
Escolher cada elemento de ordem k.
Desta forma:
8,700  2,262.
2,000
10,000
   8,700  2,262.
2,000
10,000
O intervalo de confiança que detém 95% dos valores é:
7,27    10,13
Amostragem por Conglomerados
Dividir em seções a área
populacional, selecionar
aleatoriamente algumas
dessas seções e tomar
todos os elementos das
mesmas.
Ou seja, 95% de chance da média estar dentro do
intervalo citado.
Intervalos de Confiança para Proporção
f  z .
2
Amostragem de Conveniência
Utilizar resultados de fácil acesso.
f (1  f )
f (1  f )
 p  f  z .
2
n
n
f – é a estimativa amostral
α – nível de significância (%)
n – tamanho da amostra
z α/2 - valor de z tabelado
Observação: Viável para amostras superiores a 30
unidades.
Exemplo:
1.6.2. Intervalos de Confiança
Intervalos de Confiança para Média
x  t .
2
s
n
   x  t .
2
Onde:
x – é a média amostral
α – nível de significância (%)
s – desvio padrão amostral
n – tamanho da amostra
t α/2 - valor de t tabelado
s
n
Entre 500 pessoas inquiridas a respeito de suas
preferências eleitorais, 260 mostravam-se favoráveis ao
candidato B. Calcular o intervalo de confiança ao nível
de 90% para a porcentagem ou proporção dos eleitores
favoráveis a B.
Tem-se:
n = 500
x = 260
1-α = 90%
Calculando-se f
f
x 260

 0,52
n 500
Da tabela obtém-se que:
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
z   1,64
da distribuição t de Student com
liberdade.
2
graus de
Desta forma:
0,52  1,64.
0,52.0,48
0,52.0,48
 p  0,52  1,64.
500
500
O intervalo de confiança que detém 90% dos valores é:
0,4834  p  0,5566
1.6.3. Testes de Hipóteses
Teste para Médias
Considere uma população da qual retiramos uma
amostra
. Estamos interessados em
realizar inferência sobre a média populacional .
Se o teste é unilateral, determinamos o ponto
crítico
tal que
.
Quando o desvio padrão populacional σ é conhecido:
Z
x  0

n
No caso de pequenas amostras (n<30) onde o desvio
padrão populacional não é conhecido.
t
x  0
s
n
Se o teste é unilateral à esquerda, determinamos o
Etapas do Teste:
1.
ponto
Estabelecer as Hipóteses:
Fixamos
. Dependendo da informação que
fornece o problema que estamos estudando, a hipótese
alternativa pode ter uma das três formas abaixo:
- H1: μ≠μ0 (teste bilateral)
- H1: μ > μ0 (teste unilateral à direita)
- H1: μ < μ0 (teste unilateral à esquerda)
2.
Fixar o nível de significância
3.
Determinar a região crítica.
a.
Se o teste é bilateral, determinamos os pontos
críticos
que
e
.
tais
a partir
tal que
.
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
A variável normal reduzida associada a
x  596,25 mL é:
z
(596,25  600,00)
 1,88
1,99
Utilizando a tabela da distribuição normal padrão,
obtemos que a área sob acurva à direita de −z vale 0,5
– 0,4699 = 0,03.
4.
Fazer os cálculos!
Exemplo:
Portanto
A cervejaria BebeBier vende cervejas em embalagens
cujos rótulos indicam um conteúdo de 600 ml. O
Instituto Nacional de Pesos e Medidas (INPM) seleciona
aleatoriamente 50 garrafas de cerveja produzidas pela
companhia, mede seu conteúdo e obtém uma média
amostral igual a 596,25 ml com desvio padrão de
14,06 ml. Com um nível de significância de 0,01, teste
a hipótese de que a cervejaria esta enganando seus
consumidores.
O que o INPM quer testar é se a quantidade média de
cerveja nas garrafas é diferente de 600 ml. Portanto,
vai se adotar como hipótese nula a hipótese de que a
quantidade média de cerveja por garrafa é igual a 600
ml. A hipótese alternativa é que a quantidade média de
cerveja por garrafa é diferente de 600mL:
H0: μ = 600mL
H1: μ ≠ 600mL
Portanto, o teste a ser feito é do tipo bilateral. Como a
amostra escolhida é grande (n > 30), o Teorema
Central do Limite nos diz que a distribuição amostral
das médias é aproximadamente normal.
Como o desvio padrão da população σ é desconhecido,
podemos estimá-lo pelo desvio padrão da amostra.
Desta forma, a distribuição amostral dos volumes
médios de cerveja por garrafa será normal com,
 x  600 mL
x 
s
n

14,06
50
 1,99
P  2x(0,03)  0,06
Como o valor P é maior que 0,01, não se pode rejeitar a
hipótese nula. Deve-se concluir que não há base
suficiente para se mover um inquérito contra
acervejaria.
O que se deve fazer num caso assim é repetir o estudo
com uma nova amostra maior.
1.7.
BIBLIOGRAFIA E REFERÊNCIAS
[1] MONTGOMERY; RUNGER. Probabilidade e
Estatística para Engenheiros. LTC: São Paulo, 2005.
[2] DE ALMEIDA, T.S. Avaliação da Integridade
Estrutural de Componente Mecânico Através de
Métodos Estatísticos: Estudo de Caso de um Eixo
de Transmissão de Potência. Dissertação de
Mestrado. Universidade Federal Fluminense. Volta
Redonda, 2015.
[3] BERTOLO. Apostila de Estatística. TMA.
Distribuições Discretas. 21 páginas. Disponível em:
ww.bertolo.pro.br. Acessado em agosto de 2016.
[4] BERTOLO. Apostila de Estatística. TMA.
Distribuições Contínuas. 45 páginas. Disponível em:
ww.bertolo.pro.br. Acessado em agosto de 2016.
[5] PORTAL ACTION. www.portalaction.com.br.
Acessado em agosto de 2016
[6] TRIOLA, M.F. Introdução à Estatística. 9ª edição.
LTC: São Paulo, 2005.
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
ANEXOS
Distribuição Normal Acumulada.
Tabela z padrão.
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0
0,50000
0,50399
0,50798
0,51197
0,51595
0,51994
0,52392
0,52790
0,53188
0,53586
0,1
0,53983
0,54380
0,54776
0,55172
0,55567
0,55962
0,56356
0,56749
0,57142
0,57535
0,2
0,57926
0,58317
0,58706
0,59095
0,59483
0,59871
0,60257
0,60642
0,61026
0,61409
0,3
0,61791
0,62172
0,62552
0,62930
0,63307
0,63683
0,64058
0,64431
0,64803
0,65173
0,4
0,65542
0,65910
0,66276
0,66640
0,67003
0,67364
0,67724
0,68082
0,68439
0,68793
0,5
0,69146
0,69497
0,69847
0,70194
0,70540
0,70884
0,71226
0,71566
0,71904
0,72240
0,6
0,72575
0,72907
0,73237
0,73565
0,73891
0,74215
0,74537
0,74857
0,75175
0,75490
0,7
0,75804
0,76115
0,76424
0,76730
0,77035
0,77337
0,77637
0,77935
0,78230
0,78524
0,8
0,78814
0,79103
0,79389
0,79673
0,79955
0,80234
0,80511
0,80785
0,81057
0,81327
0,9
0,81594
0,81859
0,82121
0,82381
0,82639
0,82894
0,83147
0,83398
0,83646
0,83891
1,0
0,84134
0,84375
0,84614
0,84849
0,85083
0,85314
0,85543
0,85769
0,85993
0,86214
1,1
0,86433
0,86650
0,86864
0,87076
0,87286
0,87493
0,87698
0,87900
0,88100
0,88298
1,2
0,88493
0,88686
0,88877
0,89065
0,89251
0,89435
0,89617
0,89796
0,89973
0,90147
1,3
0,90320
0,90490
0,90658
0,90824
0,90988
0,91149
0,91309
0,91466
0,91621
0,91774
1,4
0,91924
0,92073
0,92220
0,92364
0,92507
0,92647
0,92785
0,92922
0,93056
0,93189
1,5
0,93319
0,93448
0,93574
0,93699
0,93822
0,93943
0,94062
0,94179
0,94295
0,94408
1,6
0,94520
0,94630
0,94738
0,94845
0,94950
0,95053
0,95154
0,95254
0,95352
0,95449
1,7
0,95543
0,95637
0,95728
0,95818
0,95907
0,95994
0,96080
0,96164
0,96246
0,96327
1,8
0,96407
0,96485
0,96562
0,96638
0,96712
0,96784
0,96856
0,96926
0,96995
0,97062
1,9
0,97128
0,97193
0,97257
0,97320
0,97381
0,97441
0,97500
0,97558
0,97615
0,97670
2,0
0,97725
0,97778
0,97831
0,97882
0,97932
0,97982
0,98030
0,98077
0,98124
0,98169
2,1
0,98214
0,98257
0,98300
0,98341
0,98382
0,98422
0,98461
0,98500
0,98537
0,98574
2,2
0,98610
0,98645
0,98679
0,98713
0,98745
0,98778
0,98809
0,98840
0,98870
0,98899
2,3
0,98928
0,98956
0,98983
0,99010
0,99036
0,99061
0,99086
0,99111
0,99134
0,99158
2,4
0,99180
0,99202
0,99224
0,99245
0,99266
0,99286
0,99305
0,99324
0,99343
0,99361
2,5
0,99379
0,99396
0,99413
0,99430
0,99446
0,99461
0,99477
0,99492
0,99506
0,99520
2,6
0,99534
0,99547
0,99560
0,99573
0,99585
0,99598
0,99609
0,99621
0,99632
0,99643
2,7
0,99653
0,99664
0,99674
0,99683
0,99693
0,99702
0,99711
0,99720
0,99728
0,99736
2,8
0,99744
0,99752
0,99760
0,99767
0,99774
0,99781
0,99788
0,99795
0,99801
0,99807
2,9
0,99813
0,99819
0,99825
0,99831
0,99836
0,99841
0,99846
0,99851
0,99856
0,99861
3,0
0,99865
0,99869
0,99874
0,99878
0,99882
0,99886
0,99889
0,99893
0,99896
0,99900
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Distribuição t-Student
Graus de Liberdade vs Probabilidade
ν/p
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0,6
0,32492
0,288675
0,276671
0,270722
0,267181
0,264835
0,263167
0,261921
0,260955
0,260185
0,259556
0,259033
0,258591
0,258213
0,257885
0,257599
0,257347
0,257123
0,256923
0,256743
0,25658
0,256432
0,256297
0,256173
0,25606
0,255955
0,255858
0,255768
0,255684
0,255605
0,7
0,726543
0,617213
0,58439
0,568649
0,55943
0,553381
0,54911
0,545934
0,54348
0,541528
0,539938
0,538618
0,537504
0,536552
0,535729
0,53501
0,534377
0,533816
0,533314
0,532863
0,532455
0,532085
0,531747
0,531438
0,531154
0,530892
0,530649
0,530424
0,530214
0,530019
0,8
1,376382
1,06066
0,978472
0,940965
0,919544
0,905703
0,89603
0,88889
0,883404
0,879058
0,87553
0,872609
0,870152
0,868055
0,866245
0,864667
0,863279
0,862049
0,860951
0,859964
0,859074
0,858266
0,85753
0,856855
0,856236
0,855665
0,855137
0,854647
0,854192
0,853767
0,9
3,077684
1,885618
1,637744
1,533206
1,475884
1,439756
1,414924
1,396815
1,383029
1,372184
1,36343
1,356217
1,350171
1,34503
1,340606
1,336757
1,333379
1,330391
1,327728
1,325341
1,323188
1,321237
1,31946
1,317836
1,316345
1,314972
1,313703
1,312527
1,311434
1,310415
0,95
6,313752
2,919986
2,353363
2,131847
2,015048
1,94318
1,894579
1,859548
1,833113
1,812461
1,795885
1,782288
1,770933
1,76131
1,75305
1,745884
1,739607
1,734064
1,729133
1,724718
1,720743
1,717144
1,713872
1,710882
1,708141
1,705618
1,703288
1,701131
1,699127
1,697261
0,975
12,7062
4,302653
3,182446
2,776445
2,570582
2,446912
2,364624
2,306004
2,262157
2,228139
2,200985
2,178813
2,160369
2,144787
2,13145
2,119905
2,109816
2,100922
2,093024
2,085963
2,079614
2,073873
2,068658
2,063899
2,059539
2,055529
2,051831
2,048407
2,04523
2,042272
0,98
15,89454
4,848732
3,481909
2,998528
2,756509
2,612242
2,516752
2,448985
2,398441
2,359315
2,32814
2,302722
2,281604
2,263781
2,24854
2,235358
2,223845
2,213703
2,204701
2,196658
2,189427
2,182893
2,176958
2,171545
2,166587
2,162029
2,157825
2,153935
2,150325
2,146966
0,995
63,65674
9,924843
5,840909
4,604095
4,032143
3,707428
3,499483
3,355387
3,249836
3,169273
3,105807
3,05454
3,012276
2,976843
2,946713
2,920782
2,898231
2,87844
2,860935
2,84534
2,83136
2,818756
2,807336
2,79694
2,787436
2,778715
2,770683
2,763262
2,756386
2,749996
QUESTÕES PARA DISCUSSÃO
Q1 Defina Estatística Descritiva.
Q2 Quais são os parâmetros para uma tabela de
agrupamento de dados?
Q3 Cite as principais medidas de tendência central.
Q4 Cite as principais medidas de dispersão.
Q5 Para pesquisar:

Média Geométrica;

Média Harmônica;

Quartil e Percentil;

Assimetria e Curtose;
Q7 Quais as diferenças entre valores absolutos e
valores relativos? Qual deles determina melhor o erro
de um sistema?
Q8 Defina probabilidade.
Q9 Qual a relação entre Probabilidade, Lógica
Proposicional e Conjuntos? Cite exemplos
apresentando o Diagrama de Euler-Venn.
Q10 O que é uma variável discreta?
Q11 Quais são as 3 principais distribuições de
probabilidade discretas? Caracterize cada uma.
Q12 O que é uma variável contínua?
Q6 Qual a principal função de um Histograma?
Q13 O que é uma Função Densidade de
Probabilidade?
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
Q14 O que é uma Função de Distribuição Acumulada?
Q15 Defina matematicamente uma distribuição
Uniforme.
Q18 Defina matematicamente uma distribuição
Exponencial. Qual é o seu principal parâmetro?
Q19 Defina Estatística Inferencial.
Q16 Defina matematicamente uma distribuição
Normal. Quais são os seus parâmetros?
Q20 Qual a importância da amostragem?
Q21 O que é Intervalo de Confiança?
Q17 O que é a tabela z? Onde e como ela pode ser
aplicada?
Q22 Como funciona um Teste de Hipótese?
EXERCÍCIOS DE FIXAÇÃO
b.
E1 Para as tabelas a seguir, obtenha a média dos
dados agrupados:
a.
Os visitantes do parque de Yellowstone
consideram uma erupção do Old Faithfull uma atração
que não deve ser perdida. A tabela a seguir apresenta
uma amostra de tempos (em minutos) decorridos entre
as erupções.
Tempo
Frequência
8
40-49
44
50-59
23
60-69
6
70-79
107
80-89
11
90-99
1
100-109
b.
Em uma faculdade, obtiveram-se amostras de
carros de estudantes, carros de professores e carros de
funcionários da faculdade com as respectivas idades
(em anos). Estas idades estão resumidas na tabela que
segue. Ache a idade média de ambos os grupos de
carros. Com base nos resultados, percebe-se alguma
diferença significativa entre as duas amostras? O que
poderia explicar isso?
Idade
Estudantes
Prof. e Func.
23
30
0-2
33
47
3-5
63
36
6-8
68
30
9-11
19
8
12-14
10
0
15-17
1
0
18-20
0
1
21-23
E2 Calcule a Média, o Desvio Padrão e a Amplitude dos
dados não agrupados:
a.
63,54
73,09
50,72
69,41
79,07
82,89
58,74
39,13
44,83
61,67
52,41
78,84
33,77
73,51
86,09
40,68
73,43
61,67
55,72
64,84
45,55
50,53
48,26
56,82
31,41
73,69
40,12
51,12
54,85
37,05
57,70
50,33
54,71
67,33
60,81
64,50
188,8
273,0
200,0
237,2
295,0
247,0
191,3
130,5
210,2
162,9
177,0
265,4
268,0
149,9
241,0
261,2
114,9
110,2
290,6
269,0
174,4
203,2
210,9
235,8
116,0
E3 Duas bolas são retiradas (sem reposição) de uma
urna que contém 2 bolas brancas e 3 bolas pretas.
Qual a probabilidade de que a 1ª seja branca e a 2ª
seja preta ?
E4 Duas bolas são retiradas (com reposição) de uma
urna que contém 2 bolas brancas e 3 bolas pretas.
Qual a probabilidade de que a 1ª seja branca e a 2ª
seja preta ?
E5 Duas bolas são retiradas (sem reposição) de uma
urna que contém 2 bolas brancas e 3 bolas pretas e 5
bolas verdes.
a.
Qual a probabilidade de que ambas sejam
verdes ?
b.
Qual a probabilidade de que ambas sejam da
mesma cor ?
E6 Um dado cúbico, não viciado, com faces numeradas
de 1 a 6, é lançado três vezes. Em cada lançamento,
anota-se o número obtido na face superior do dado,
formando-se uma sequência (a, b, c). Qual é a
probabilidade de que b seja sucessor de a ou que c
seja sucessor de b?
a.
4/27
b.
11/54
c.
7/27
d.
10/27
e.
23/54
E7 O controle de qualidade de uma empresa fabricante
de telefones celulares aponta que a probabilidade de
um aparelho de determinado modelo apresentar defeito
de fabricação é de 0,2%. Se uma loja acaba de vender
4 aparelhos desse modelo para um cliente, qual é a
probabilidade de esse cliente sair da loja com
exatamente dois aparelhos defeituosos?
a.
2 × (0,2%)4.
b.
4 × (0,2%)2.
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
c.
d.
e.
6 × (0,2%)2 × (99,8%)2.
4 × (0,2%).
6 × (0,2%) × (99,8%).
E8 Qual é a probabilidade de, selecionado ao acaso,
um anagrama da palavra ANE, iniciar-se por
consoante?
a.
1/3
b.
1/6
c.
2/3
d.
5/8
e.
1/2
E9 Suponha que a probabilidade dos pais terem um
filho(a) com cabelos loiros seja ¼. Se houverem 6
crianças na família, qual é a probabilidade de que
metade delas terem cabelos loiros? Dica: Use a
distribuição binomial.
E10 Se a probabilidade de atingir um alvo num único
disparo é 0,3, qual é a probabilidade de que em 4
disparos o alvo seja atingido no mínimo 3 vezes? Dica:
Use a distribuição binomial.
E11 Trace uma curva normal e sombreie a área
desejada obtendo então a informação.
a.
Área à direita de Z = 1
b.
Área à esquerda de Z = 1
c.
Área entre Z = 0 e Z = 1,5
d.
Área entre Z = -0,56 e Z = -0,2
e.
Área entre Z = 0,5 e Z = 0,5
f.
Área entre Z = 0 e Z = -2,5
E12 Usando a tabela da distribuição normal,
determine os valores de Z que correspondem às
seguintes áreas:
a.
Área de 0,0505 à esquerda de Z.
b.
Área de 0,0228 à direita de Z
c.
Área de 0,0228 à esquerda de Z
d.
Área entre 0 e 0,4772.
E13 Consultando a tabela, determine a probabilidade
de certo valor padronizado de “Z” estar entre Z0 = -1,20
e Z1 = 2,00. Desenhe o gráfico.
E14 Dado uma população com média 25 e desviopadrão 2 tem a distribuição normal, determine os
valores de Z para os seguintes valores (x) da
população:
a.
23
b.
23,5
c.
24
d.
25,2
e.
25,5
E15 Determine a probabilidade de certo valor
padronizado de “Z” estar entre Z0 = -1,30. Desenhe o
gráfico.
E16 Uma população normal tem média 40 e desviopadrão 3. Determine os valores da população
correspondentes aos seguintes de Z:
a.
0,10
b.
2,00
c.
0,75
d.
-3,00
e.
-2,53
E17 Uma distribuição normal de eixos tem um
diâmetro médio de 50 mm e desvio padrão igual à 5
mm. Que percentagem de eixos tem diâmetro entre 40
e 50?
E18 Em uma fábrica, colhida uma amostra de 30
peças para avaliação, obtiveram as seguintes
informações sobre o diâmetro das peças:
x =13,13 e s² = 2,05. Construir um intervalo de
confiança para a média sendo α = 5%.
E19 Uma centena de componentes foi ensaiada e 93
deles funcionaram mais de 500 horas. Determinar um
intervalo de 95% para a proporção.
PROBLEMAS E APLICAÇÕES
P1 Foi feito um estudo para determinar como as
pessoas obtêm emprego. A tabela que segue relaciona
dados de 400 pessoas escolhidas aleatoriamente. Os
dados se baseiam em resultados do National Center for
Career Stratagies (Centro Nacional de Estratégias de
Carreiras).
Fontes de Trabalho que Responde à
Frequência
Pesquisa
Anúncios do Tipo “Procura-se”
56
Firmas de Pesquisa
44
Rádio e Televisão
280
Envio de Correspondência em Massa
20
a.
Construa um gráfico de Pareto para o conjunto
de dados em questão. Qual seria a abordagem mais
eficiente para uma pessoa que procura um emprego?
b.
Construa um gráfico setorial acerca dos dados
e o compare o gráfico de Pareto. Qual deles representa
a importância relativa das fontes de trabalho?
P2 Em um estudo de seguro de acidentes com veículos
motorizados no estado de Nova York, classificam-se as
colisões fatais de acordo com a hora do dia, com os
resultados constantes da tabela a seguir.
Controle Estatístico de Processos
Profº Túlio de Almeida, M.Sc.
a.
Construa um gráfico Setorial e um
Histograma.
b.
Qual dos dois ilustra melhor os dados? Por
quê?
c.
Como o período de 04:00 às 06:00 da manhã é
o que apresenta menor número de colisões, podemos
concluir que esse período é o mais seguro para dirigir?
Por que sim ou por que não?
P3 Retirando-se uma carta de um baralho de 52
cartas, qual a probabilidade da carta retirada ser ou
um ÁS ou uma carta de COPAS?
P4 Em uma pesquisa realizada com 10.000
consumidores sobre a preferência da marca de sabão
em pó, verificou-se que: 6500 utilizam a marca X;
5500 utilizam a marca Y; 2000 utilizam as duas
marcas. Foi sorteada uma pessoa desse grupo e
verificou-se que ela utiliza a marca X. Qual a
probabilidade dessa pessoa ser também usuária da
marca Y?
P5 Supõe-se que a vida média de um circuito
eletrônico tenha uma distribuição normal com média
de 50.000 horas e desvio-padrão de 8.000 horas. Qual
a probabilidade de um circuito escolhido ao acaso
durar mais de 55.000 horas?
P6 O gerente da Loja Consul do “Shopping do Vale do
Aço” fez uma coleta aleatória do tempo de permanência
de clientes na fila de pagamento e descobriu que o
tempo médio é igual á 6 minutos e o desvio-padrão
igual a 1 minuto. Para diminuir a ansiedade de seus
clientes na fila, ele deseja dispor um quadro indicativo
com o tempo previsto para o atendimento. Supondo
que estes tempos tenha uma distribuição normal, se
for disposto que o tempo de atendimento será de 8
minutos, qual a percentagem máxima de clientes que
poderão reclamar com o gerente?
P7 Dois tornos CNC produzem o mesmo tipo de peça,
porém com especificações de medidas diferentes. Um
lote produzido pelo torno “A” tem diâmetro médio de 50
mm e DP de 3 mm. O conjunto de peças produzidos
pelo torno “B” tem diâmetro médio de 80 mm e DP de 6
mm. As peças produzidas pela máquina “A” que se
afastarem da média por mais de 7 mm serão
rejeitados. As peças produzidas pela máquina “B” que
se afastarem da média por mais de 15mm serão
rejeitadas. Supondo que as distribuições da variável
sejam normais:
a.
Qual é o torno que produz maior quantidade
de peças defeituosas?
b.
Qual o número de peças defeituosas
produzidas por “B” se o lote for de 1.000 peças.
P8 A força de compressão do concreto está sendo
testada por um engenheiro civil. Ele testa 12 amostras
e obtém os seguintes resultados:
2216
2237
2249
2204
2225
2301
2281
2263
2318
2255
2275
2295
Assumindo-se a distribuição normal pede-se:
a.
Construa o I.C. (95%) para a força média.
b.
Construa o I.C. (99%) para a força média.
c.
Ao nível de 5% de significância, verificar se a
verdadeira média da força de compressão difere de
2280. Realizar o teste t para uma média.
d.
Repetir o item c, porém para α=1%
e.
Repetir o item c, porém verificando se a
verdadeira força média difere de 2300.
f.
Compare as conclusões usando-se de I.C. e
testes de hipóteses.
P9 Tintas para marcação de asfalto em rodovias são
oferecidas em duas cores: branca e amarela. O tempo
de secagem destas tintas é muito interessante, e
especificamente, suspeita-se que a tinta amarela seca
mais rápido que a branca. Amostras foram obtidas
para a medição dos tempos de secagem (em minutos),
em condições reais das duas tintas:
Tinta
Branca
00:00-02:00
02:00-04:00
04:00-06:00
06:00-08:00
08:00-10:00
10:00-12:00
12:00-14:00
14:00-16:00
16:00-18:00
18:00-20:00
20:00-22:00
22:00-00:00
Número de
Acidentes Fatais
194
149
100
131
119
160
152
221
230
211
223
178
120
132
123
122
140
110
120
107
Tinta
Amarela
P.M.
A.M.
Hora
126
124
116
125
109
130
125
117
Assumindo-se a distribuição normal pede-se:
a.
Obtenha o I.C. (95%) para o tempo médio de
secagem de cada tinta.
b.
Realize um teste de hipótese para responder as
questões apresentadas no enunciado do problema. Use
α = 5%.