CSim-15 - Resumo de Geometria Espacial

Geometria Espacial 04
Prof. Valdir
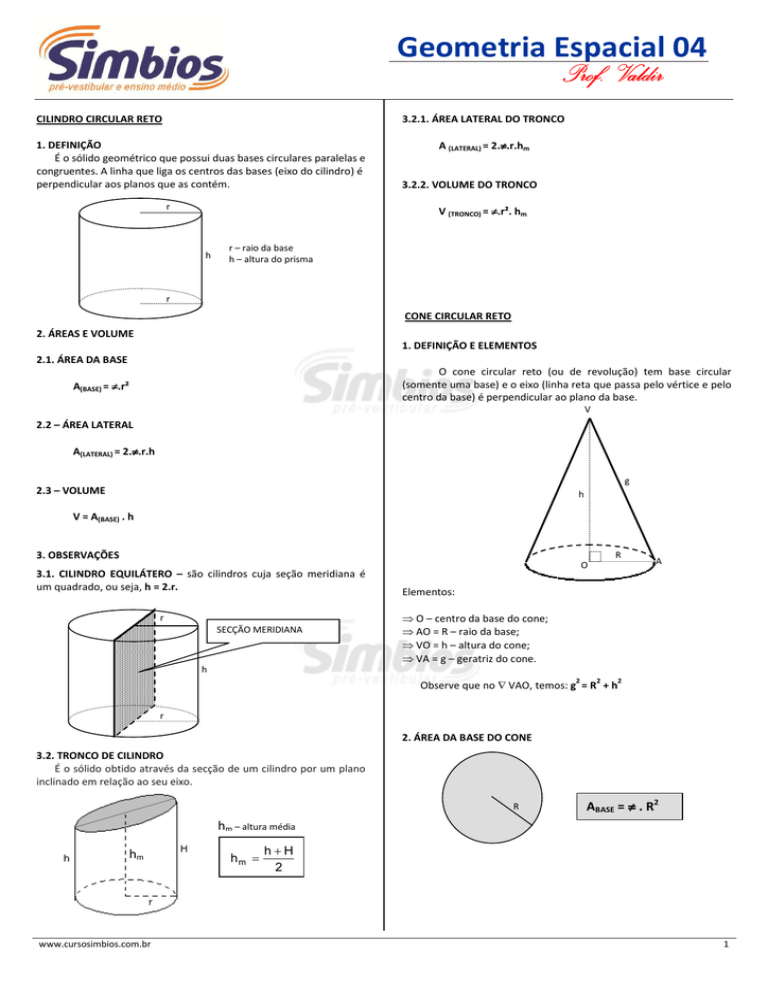
CILINDRO CIRCULAR RETO
3.2.1. ÁREA LATERAL DO TRONCO
1. DEFINIÇÃO
É o sólido geométrico que possui duas bases circulares paralelas e
congruentes. A linha que liga os centros das bases (eixo do cilindro) é
perpendicular aos planos que as contém.
r
A (LATERAL) = 2.π
π.r.hm
3.2.2. VOLUME DO TRONCO
V (TRONCO) = π.r². hm
h
r – raio da base
h – altura do prisma
r
CONE CIRCULAR RETO
2. ÁREAS E VOLUME
1. DEFINIÇÃO E ELEMENTOS
2.1. ÁREA DA BASE
O cone circular reto (ou de revolução) tem base circular
(somente uma base) e o eixo (linha reta que passa pelo vértice e pelo
centro da base) é perpendicular ao plano da base.
A(BASE) = π.r²
V
2.2 – ÁREA LATERAL
A(LATERAL) = 2.π
π.r.h
g
2.3 – VOLUME
h
V = A(BASE) . h
R
3. OBSERVAÇÕES
O
3.1. CILINDRO EQUILÁTERO – são cilindros cuja seção meridiana é
um quadrado, ou seja, h = 2.r.
r
SECÇÃO MERIDIANA
A
Elementos:
⇒ O – centro da base do cone;
⇒ AO = R – raio da base;
⇒ VO = h – altura do cone;
⇒ VA = g – geratriz do cone.
h
Observe que no ∇ VAO, temos: g = R + h
2
2
2
r
2. ÁREA DA BASE DO CONE
3.2. TRONCO DE CILINDRO
É o sólido obtido através da secção de um cilindro por um plano
inclinado em relação ao seu eixo.
R
ABASE = π . R2
hm – altura média
hm
www.cursosimbios.com.br
hm =
h+H
2
1
TRONCO DE PIRÂMIDE E DE CONE
3. ÁREA LATERAL DO CONE CIRCULAR RETO
A planificação da superfície lateral do cone circular reto
resulta em um setor circular, como mostra a figura abaixo.
V
Ab
V1
V
h1
V2
α
H
r
⇒
a
g
g
A
A
R
B
b
2π
πR
B
h
V
SUPERFÍCIE
LATERAL
AB
Da figura, podemos ter:
2.π .R = α . g ⇒ α =
2πR
g
1. ELEMENTOS
A área lateral será:
2.π.R.g
⇒ ALATERAL = π . R. g
2
ALATERAL =
4. ÁREA TOTAL DO CONE
ATOTAL = A BASE + ALATERAL
5. VOLUME DO CONE
V=
A BASE .h
3
H – Altura da pirâmide(cone) maior;
h1 – altura da pirâmide(cone) menor;
h – altura do tronco de pirâmide (tronco de cone);
a – aresta da base da pirâmide menor;
b – aresta da base da pirâmide maior;
r – raio da base do cone menor;
R – raio da base do cone maior;
Ab – área da base menor;
AB – área da base maior;
V1 – volume da pirâmide (cone) menor;
V2 – volume da pirâmide (cone) maior;
V – volume do tronco de pirâmide (tronco de cone).
2. VOLUME DO TRONCO
Observando a proporcionalidade das duas figuras, teremos:
6. SECÇÃO MERIDIANA
Obs.: Se a secção meridiana
for um triângulo equilátero
(g = 2R), então o cone é
denominado
CONE EQUILÁTERO.
g
H
2
=
Ab
AB
h 13
H
3
=
V1
V2
Para determinar o volume do tronco, basta retirar da pirâmide
maior o volume da pirâmide menor. Ou seja:
h
g
h 12
h1 a
=
H
b
VTRONCO = VPIRÂMIDE MAIOR – VPIRÂMIDE MENOR
R
Trabalhando a idéia acima e as proporções anteriormente
mencionadas, teremos:
R
VTRONCO =
Área da secção meridiana:
www.cursosimbios.com.br
h
(A B + A b + A B .A b )
3
A SECÇÃO= R. h
2
Para o tronco de cone:
g
r
2π
π.r
SUPERFÍCIE LATERAL DO
TRONCO DE CONE
2.π
π .R
R
Ab = π.r² e AB = π.R²
Para determinar a área da superfície lateral do tronco de cone, basta
observar que a mesma é um setor de coroa. Neste caso, teremos:
 2.π.R + 2.π.r 
A LATERAL = 
.g
2


.
Simplificando, teremos:
A LATERAL = π.g.(R + r)
www.cursosimbios.com.br
3