mat discreta ii

MATEMÁTICA DISCRETA II-Profº Marcos do Nascimento
CÁPITULO I- VETORES E MATRIZES
1.1 INTRODUÇÃO
Dados são frequentemente organizados em arrays, ou seja, conjunto cujos elementos são indexados por um ou mais
índices. Normalmente, um array unidimensional é chamado de vetor, e um array bidimensional é chamado de matriz,
em que a dimensão, neste caso, denota o número de índices.
1.2 VETORES
Vamos nos referenciar a uma lista de números a1 , a 2 ,K, a n , como um vetor u . Um tal vetor é denotado por:
u = (a1 , a2 , K , an )
Os números ai são ditos componentes ou elementos de u . Se todos os ai = 0 , então u é dito vetor zero.
Dois vetores u e v são iguais se possuem o mesmo número de componentes e os componentes
correspondentes são iguais. Exemplos:
• u = (3,−4,5) : vetor com três componentes;
• v = (−2,6,−8,3) : vetor com quatro componentes;
1.2.1 Operações com Vetores
Considere dois vetores arbitrários, u e v com o mesmo número de componentes, u = (a1 , a2 , K , an ) e
v = (b1 , b2 ,K, bn ) . Assim:
•
u + v = (a1 + b1 , a2 + b2 ,K, a n + bn ) → Soma de u e v
•
k ⋅ u = (ka1 , ka2 ,K, k n ) → Produto por Escalar
•
u = u ⋅ u = a1 + a2 + K + a n → Norma do Vetor u
•
u ⋅ v = a1 ⋅ b1 + a 2 ⋅ b2 +,K, a n ⋅ bn → Produto Interno
•
•
− u = −1 ⋅ u
u − v = u + ( −v )
2
2
2
1.2.2 Vetores Coluna
Às vezes uma lista de números é escrita no sentido vertical em vez de horizontal, sendo chamada de vetor
coluna. Neste contexto, os vetores escritos na forma horizontal são chamados de vetores linha. As
operações definidas para os vetores linhas são definidas de maneira análoga para vetores coluna.
3 
u = 2 → Vetor coluna com 3 componentes
5 
− 9 
v =   → Vetor coluna com 2 componentes
− 4
1.3 MATRIZES
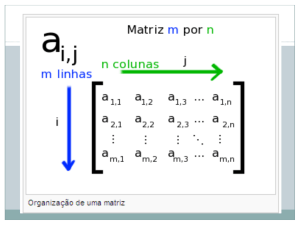
Uma matriz A é um array retangular de números representado na forma:
a11 a12 L a1n 

a 2 a 22 L a 2 n 
A= 1
M M O M 


a m1 a m 2 L a mn  m×n
1
As m listas horizontais de números são chamadas de linhas da matriz A , já as n listas verticais são
chamadas de colunas. Assim o elemento aij , chamado de elemento ij, aparece na linha i e na coluna j de A .
[ ]
Frequentemente denota-se uma matriz simplesmente escrevendo A = aij . Uma matriz com m linhas e n
colunas é dita matriz de ordem m por n e escreve-se m × n . O par de números m e n é chamado de dimensão
de A . Duas matrizes A e B são iguais se possuem a mesma dimensão e se seus elementos correspondentes
são iguais.
1.3.1 Operações com Matrizes
• Adição
[ ]
[ ]
Sejam A = aij e B = bij duas matrizes de mesma dimensão. A soma de A e B denotada por A + B é a
matriz obtida pela adição dos elementos correspondentes de A e B .
• Multiplicação por Escalar
O produto de uma matriz A por um escalar k , escreve-se k ⋅ A é uma matriz obtida multiplicando-se
cada elemento aij da matriz A pelo escalar k .
Observação:
− A = −1 ⋅ A
A − B = A + (− B)
• Multiplicação de Matrizes
Suponha que A = [aik ] e B = bkj são matrizes em que o número de colunas de A é igual ao número de
[ ]
linhas de B , isto é, A é uma de ordem m × p e B é matriz de ordem p × n . O produto A ⋅ B será uma
matriz C de ordem m × n cujo elemento cij é obtido pela multiplicação da i-ésima linha de A pela jésima coluna de B , da seguinte forma:
p
cij = ai1 ⋅ b1 j + ai 2 ⋅ b2 j + L + aip ⋅ b pj = ∑ aik ⋅ bkj
k =1
1.3.2 Propriedades
Sejam A, B e C matizes de mesma dimensão, e sejam k e k ' escalares. Então:
I) (A+B)+C=A+(B+C)
II) A+0=0+A
III) A+(-A)=(-A)+0=A
IV) A+B=B+A
V) k(A+B)=kA+kB
VI) ( k + k ' )A=kA+ k ' A
VII) (kk ' ) A = k (k ' A)
VIII) 1A=A
1.3.3 Matriz Transposta
A transposta de uma matriz A , denotada por AT é a matriz obtida pela colocação das linhas de A, em
ordem, no lugar das colunas. Se A é uma matriz de ordem m × n , então AT terá ordem n × m . Exemplo:
2
A = 5
4
6
7
9 
→
2
AT = 
6
5
7
4
9 
1.3.4 Matrizes Quadradas
Uma matriz com o mesmo número de linhas e colunas é chamada matriz quadrada. Uma matriz quadrada
com n linhas e n colunas é chamada de matriz de ordem n. A diagonal principal de uma matriz quadrada de
ordem n, consiste nos elementos: a11 , a22 , a33 , L , ann . A matriz identidade de ordem n, denotada I n é a
matriz quadrada que possui 1 ao longo da diagonal principal e zero dos demais elementos. A matriz
2
identidade desempenha um papel importante na multiplicação de matrizes, assim como o número 1 o faz na
multiplicação usual de números, pois:
AI = IA = A
• Álgebra de Matrizes Quadradas
Seja A uma matriz quadrada qualquer. Podemos multiplicar A por ela mesma. Na verdade podem-se
formar todas as potências não negativas de A da seguinte forma:
A2 = A ⋅ A ,
A3 = A 2 ⋅ A ,
A 4 = A3 ⋅ A , ... , A n+1 = A n ⋅ A
1.3.5 Matrizes Inversíveis (Não singulares) e Inversas
Uma matriz quadrada A é denominada inversível(ou não singular) se existe uma matriz B com a
propriedade que:
AB = BA = I
em que I é matriz identidade. Tal matriz B é única e é chamada matriz inversa de A e denotada por A −1 .
BIBLIOGRAFIA
LIPSCHUTZ, S.; LIPSON, M.. Matemática Discreta. 2ª ed., São Paulo: Bookman, 2004.
MENEZES, P. B.. Matemática Discreta para Computação e Informática. São Paulo: 3ª ed. Bookman, 2010.
GERSTING, Judith L, Fundamentos Matemáticos para Ciência da Computação. 5ª Ed. São Paulo: LTC, 2004.
3