Solução

www.fisicaexe.com.br
Sobre um plano inclinado de 30o em relação à
horizontal, desliza sem atrito uma massa m 1 presa a uma
outra massa m 2 . Abandonando o sistema a partir do
repouso a massa m 2 sobe 250 m em 20 s. Calcular a
relação m1/m2. Adote g = 10 m/s 2.
Dados do problema
•
•
•
•
•
•
•
massa do bloco 1:
ângulo de inclinação do plano:
massa do bloco 2:
deslocamento do bloco 2:
velocidade inicial do sistema:
intervalo de tempo de subida:
aceleração da gravidade:
m 1;
θ = 30o;
m 2;
ΔS = 250 m;
v 0 = 0;
Δ t = 20 s
g = 10 m/s 2.
Esquema do problema
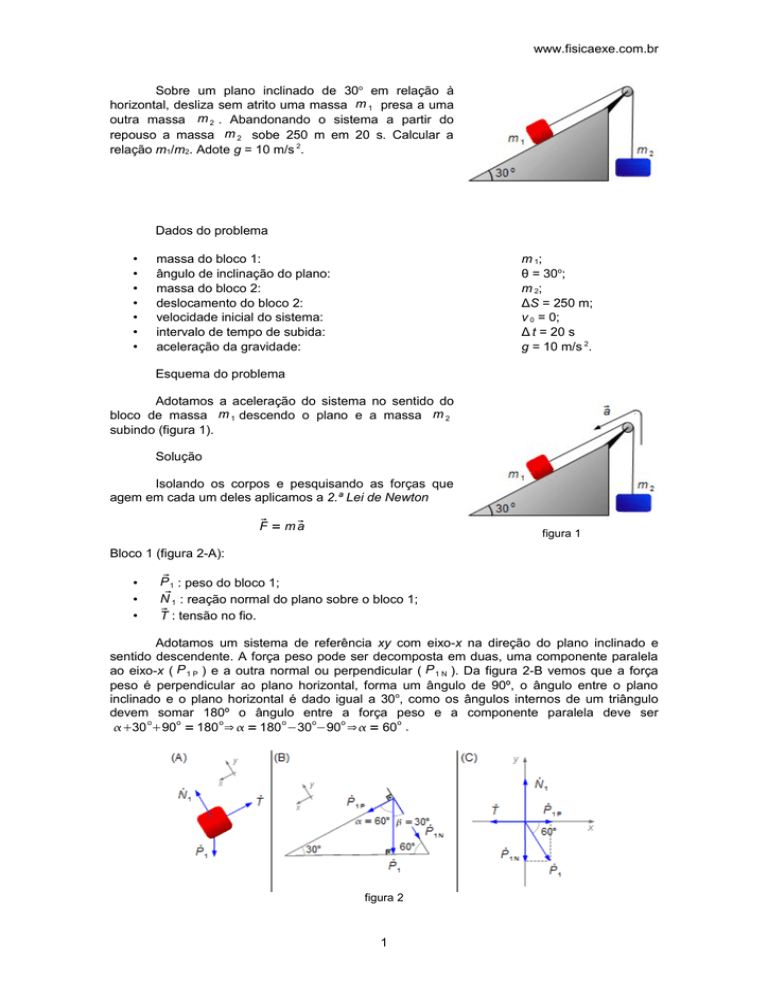
Adotamos a aceleração do sistema no sentido do
bloco de massa m 1 descendo o plano e a massa m 2
subindo (figura 1).
Solução
Isolando os corpos e pesquisando as forças que
agem em cada um deles aplicamos a 2.ª Lei de Newton
 = m
F
a
figura 1
Bloco 1 (figura 2-A):
•
•
•
P1 : peso do bloco 1;
N1 : reação normal do plano sobre o bloco 1;
 : tensão no fio.
T
Adotamos um sistema de referência xy com eixo-x na direção do plano inclinado e
sentido descendente. A força peso pode ser decomposta em duas, uma componente paralela
ao eixo-x ( P 1 P ) e a outra normal ou perpendicular ( P 1 N ). Da figura 2-B vemos que a força
peso é perpendicular ao plano horizontal, forma um ângulo de 90º, o ângulo entre o plano
inclinado e o plano horizontal é dado igual a 30o, como os ângulos internos de um triângulo
devem somar 180º o ângulo entre a força peso e a componente paralela deve ser
o
o
o
o
o
o
o
30 90 = 180 ⇒  = 180 −30 −90 ⇒  = 60 .
figura 2
1
www.fisicaexe.com.br
As componentes do peso nas direções x e y são perpendiculares entre si, no triângulo
à direita temos que o ângulo entre as força peso e a componente do peso na direção y é
o
o
o
o
 = 90 −⇒ 90 −60 ⇒ 30 .
Desenhando o vetores num sistema de eixos coordenados na direção y a componente
normal da força peso e a reação normal se anulam, não há movimento nesta direção. Na
direção x da 2.ª Lei de Newton temos
P 1 P−T = m 1 a
(I)
Da figura 2-C a componente do peso na direção x é escrita como
P 1 P = P 1 cos 60
o
(II)
sendo o módulo da força peso dado por
P1 = m 1 g
(III)
substituindo (III) em (II) e este em (I), obtemos
o
m 1 g cos60 −T = m 1 a
(IV)
Bloco 2 (figura 3):
•
•
 2 : peso do bloco 2;
P
 : tensão no fio.
T
Adotamos o sentido positivo para cima no mesmo sentido da aceleração. Na
direção horizontal não há forças agindo no bloco, na direção vertical da 2.ª Lei de
Newton obtemos
T −P 2 = m 2 a
figura 3
(V)
O módulo da força peso é dado por
P2 = m 2 g
(VI)
T −m 2 g = m 2 a
(VII)
substituindo (VI) em (V), obtemos
Somando a expressão (IV) de (VII) temos a aceleração do sistema
∣
o
m 1 g cos60 −T = m 1 a
T −m 2 g = m 2 a
O
m 1 g cos 60 −m 2 g = m 1 am 2 a
colocando a aceleração da gravidade em evidência do lado esquerdo da igualdade e a
aceleração a do lado direito
o
g  m 1 cos60 −m 2  = a  m 1 m 2 
a =g

o
m 1 cos60 − m 2
m 1 m 2

(VIII)
Da Cinemática Escalar usamos a equação horária do Movimento Retilíneo
Uniformemente Variado (M.R.U.V.)
2
www.fisicaexe.com.br
a 2
t
2
a 2
S−S 0 = V 0 t  t
2
S = S 0 V 0 t 
sendo Δ S = S−S 0 e usando o valor da
aceleração da expressão (VIII), escrevemos
ΔS = V0 t

o

figura 4
m 1 cos60 −m 2 2
1
g
t
2
m 1 m 2
o
substituindo os valores dados no problema e sendo cos 60 =
1
, Δ t = t −t 0 ⇒ 20 = t −0 ⇒
2
⇒ t = 20 s , temos
1
250 = 0 .20 .10.
2


1
m 1 −m 2
2
2
. 20
m 1 m 2


m 1 −2 m 2
2
250 = 05.
. 400
m 1m 2
[
]
m 1 −2 m 2
.2 000
2  m 1 m 2 
m 1 −2 m 2
250
=
2 000 2 m 12 m 2
250 =
do lado esquerdo da igualdade dividimos o numerador e o denominador por 250, obtendo a
simplificação
m 1−2 m 2
250: 250
=
2 000 : 250 2 m 1 2 m 2
m 1 −2 m 2
1
=
8 2 m 12 m 2
multiplicando em “cruz”
2 m 1 2 m 2 = 8 .  m 1 −2 m 2 
2 m 1 2m 2 = 8 m 1 −16 m 2
2 m 2 16 m 2 = 8 m 1 −2 m 1
18 m 2 = 6 m 1
m 1 18
=
m2
6
m1
=3
m2
3