Professora FLORENCE

Professora FLORENCE
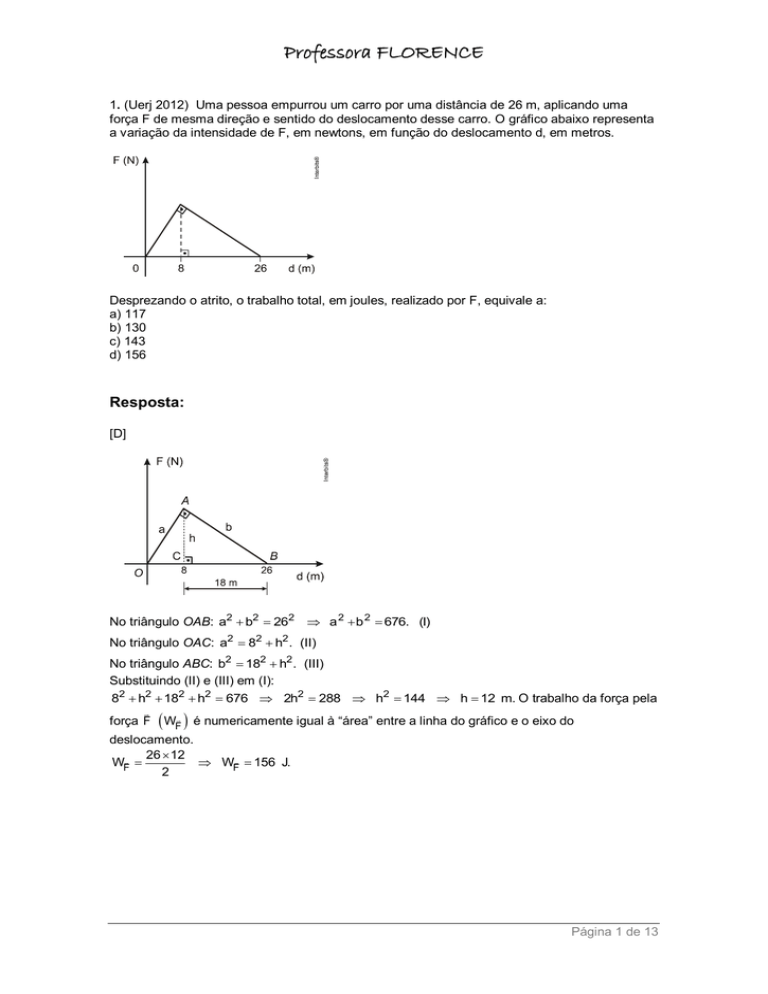
1. (Uerj 2012) Uma pessoa empurrou um carro por uma distância de 26 m, aplicando uma
força F de mesma direção e sentido do deslocamento desse carro. O gráfico abaixo representa
a variação da intensidade de F, em newtons, em função do deslocamento d, em metros.
Desprezando o atrito, o trabalho total, em joules, realizado por F, equivale a:
a) 117
b) 130
c) 143
d) 156
Resposta:
[D]
No triângulo OAB: a2  b2  262  a 2  b 2  676. (I)
No triângulo OAC: a2  82  h2 . (II)
No triângulo ABC: b2  182  h2 . (III)
Substituindo (II) e (III) em (I):
82  h2  182  h2  676  2h2  288  h2  144  h  12 m. O trabalho da força pela
força F
 WF  é numericamente igual à “área” entre a linha do gráfico e o eixo do
deslocamento.
26  12
WF 
 WF  156 J.
2
Página 1 de 13
Professora FLORENCE
2. (G1 - ifba 2012) Um corpo é abandonado do alto de um plano inclinado, conforme a figura
2
abaixo. Considerando as superfícies polidas ideais, a resistência do ar nula e 10 m/s como a
aceleração da gravidade local, determine o valor aproximado da velocidade com que o corpo
atinge o solo:
a) v = 84 m/s
b) v = 45 m/s
c) v = 25 m/s
d) v = 10 m/s
e) v = 5 m/s
Resposta:
[D]
Pela conservação da Energia Mecânica:
EMec0  EMec A
 m g h
m v2
2
 v  2 g h  2 10  5  
v  10 m / s.
3. (Ufsm 2012) Um estudante de Educação Física com massa de 75 kg se diverte numa rampa de skate
de altura igual a 5 m. Nos trechos A, B e C, indicados na figura, os módulos das velocidades do estudante
são vA , vB e vC, constantes, num referencial fixo na rampa. Considere g = 10 m/s2 e ignore o atrito.
São feitas, então, as seguintes afirmações:
I. vB = vA + 10 m/s.
II. Se a massa do estudante fosse 100 kg, o aumento no módulo de velocidade vB seria 4/3 maior.
III. vC = vA.
Está(ão) correta(s)
a) apenas I.
b) apenas II.
c) apenas III.
d) apenas I e II.
e) apenas I e III.
Página 2 de 13
Professora FLORENCE
Resposta:
[C]
Analisando cada uma das afirmações:
I. Incorreta. O sistema é conservativo. Então, tomando como referencial o plano horizontal que
passa pelo ponto B. temos:
A
EB
Mec  EMec

2
mvB
mv 2A
 mg h 
2
2
 vB  v 2A  2 g h  vB  v 2A  2 10  5  
vB  v 2A  100
II. Incorreta. Como foi demonstrado na afirmação anterior, a velocidade não depende da
massa.
III. Correta. Como os pontos A e C estão na mesma altura, as velocidades nesses pontos tem
mesmo valor: v C = vA.
4. (G1 - ifsc 2012) O bate-estacas é um dispositivo muito utilizado na fase inicial de uma
construção. Ele é responsável pela colocação das estacas, na maioria das vezes de concreto,
que fazem parte da fundação de um prédio, por exemplo. O funcionamento dele é
relativamente simples: um motor suspende, através de um cabo de aço, um enorme peso
(martelo), que é abandonado de uma altura, por exemplo, de 10 m, e que acaba atingindo a
estaca de concreto que se encontra logo abaixo. O processo de suspensão e abandono do
peso sobre a estaca continua até a estaca estar na posição desejada.
É CORRETO afirmar que o funcionamento do bate-estacas é baseado no princípio de:
a) transformação da energia mecânica do martelo em energia térmica da estaca.
b) conservação da quantidade de movimento do martelo.
c) transformação da energia potencial gravitacional em trabalho para empurrar a estaca.
d) colisões do tipo elástico entre o martelo e a estaca.
e) transformação da energia elétrica do motor em energia potencial elástica do martelo.
Resposta:
[C]
Durante a queda do martelo, há transformação de energia potencial gravitacional em energia
cinética. No contanto com a estaca, o martelo aplica força sobre ela. Essa força realiza
trabalho, empurrando a estaca.
Página 3 de 13
Professora FLORENCE
5. (Unesp 2012) Uma pessoa, com 80 kg de massa, gasta para realizar determinada atividade
física a mesma quantidade de energia que gastaria se subisse diversos degraus de uma
escada, equivalente a uma distância de 450 m na vertical, com velocidade constante, num local
onde g  10 m/s 2 . A tabela a seguir mostra a quantidade de energia, em joules, contida em
porções de massas iguais de alguns alimentos.
Alimento
espaguete
pizza de mussarela
chocolate
batata frita
castanha de caju
Energia por porção
(kJ)
360
960
2160
1000
2400
Considerando que o rendimento mecânico do corpo humano seja da ordem de 25%, ou seja,
que um quarto da energia química ingerida na forma de alimentos seja utilizada para realizar
um trabalho mecânico externo por meio da contração e expansão de músculos, para repor
exatamente a quantidade de energia gasta por essa pessoa em sua atividade física, ela deverá
ingerir 4 porções de
a) castanha de caju.
b) batata frita.
c) chocolate.
d) pizza de mussarela.
e) espaguete.
Resposta:
[E]
Dados: m = 80 kg; h = 450 m; g = 10 m/s2;  = 25% = 0,25 = 1/4.
A energia útil (EU) nessa atividade a energia potencial gravitacional adquirida pela pessoa.
EU  mgh  80 10  450   360.000 J  EU  360 kJ.
A energia total (ET) liberada pelo organismo nessa atividade é:
E
E
360
  U  ET  U 
 ET  4  360  
1
ET

4
ET  1.440 J.
Consultando a tabela dada, concluímos que essa quantidade de energia corresponde à de 4
porções de espaguete.
6. (Unicamp 2012) As eclusas permitem que as embarcações façam a transposição dos
desníveis causados pelas barragens. Além de ser uma monumental obra de engenharia
hidráulica, a eclusa tem um funcionamento simples e econômico. Ela nada mais é do que um
elevador de águas que serve para subir e descer as embarcações. A eclusa de Barra Bonita,
no rio Tietê, tem um desnível de aproximadamente 25 m. Qual é o aumento da energia
potencial gravitacional quando uma embarcação de massa m  1,2  104 kg é elevada na
eclusa?
a) 4,8  102 J
b) 1,2  105 J
c) 3,0  105 J
d) 3,0  106 J
Página 4 de 13
Professora FLORENCE
Resposta:
[D]
EP  mgh  1,2  104  10  25  3  106 J.
7. (Uem 2012) Sobre a energia mecânica e a conservação de energia, assinale o que for
correto.
01) Denomina-se energia cinética a energia que um corpo possui, por este estar em
movimento.
02) Pode-se denominar de energia potencial gravitacional a energia que um corpo possui por
se situar a uma certa altura acima da superfície terrestre.
04) A energia mecânica total de um corpo é conservada, mesmo com a ocorrência de atrito.
08) A energia total do universo é sempre constante, podendo ser transformada de uma forma
para outra; entretanto, não pode ser criada e nem destruída.
16) Quando um corpo possui energia cinética, ele é capaz de realizar trabalho.
Resposta:
01 + 02 + 08 + 16 = 27.
01) Correta. Energia cinética é energia mecânica associada ao movimento.
02) Correta. Energia potencial gravitacional é energia mecânica de posição, dependendo,
portanto, da altura em relação ao plano horizontal de referência.
04) Incorreta. A força de atrito pode atuar tanto como força dissipativa (transformando energia
mecânica em térmica) ou como força incrementativa (transferindo energia mecânica ao
corpo).
08) Correta. É o que afirma o princípio da conservação da energia.
16) Correta. De acordo com o teorema da energia cinética, o trabalho da resultante é igual à
variação da energia cinética. OBS: nessa afirmativa há uma imprecisão, pois em Física o
trabalho é realizado pela força que o corpo aplica e não pelo corpo.
8. (G1 - ifsp 2012) Arlindo é um trabalhador dedicado. Passa grande parte do tempo de seu
dia subindo e descendo escadas, pois trabalha fazendo manutenção em edifícios, muitas vezes
no alto.
Página 5 de 13
Professora FLORENCE
Considere que, ao realizar um de seus serviços, ele tenha subido uma escada com velocidade
escalar constante. Nesse movimento, pode-se afirmar que, em relação ao nível horizontal do
solo, o centro de massa do corpo de Arlindo
a) perdeu energia cinética.
b) ganhou energia cinética.
c) perdeu energia potencial gravitacional.
d) ganhou energia potencial gravitacional.
e) perdeu energia mecânica.
Resposta:
[D]
A expressão da energia potencial é: EPot = m g h. Se ele está subindo, a altura está
aumentando, portanto, o centro de massa do corpo do Arlindo está ganhando energia
potencial.
9. (Espcex (Aman) 2011) Um bloco, puxado por meio de uma corda inextensível e de massa
desprezível, desliza sobre uma superfície horizontal com atrito, descrevendo um movimento
retilíneo e uniforme. A corda faz um ângulo de 53° com a horizontal e a tração que ela
transmite ao bloco é de 80 N. Se o bloco sofrer um deslocamento de 20 m ao longo da
superfície, o trabalho realizado pela tração no bloco será de:
(Dados: sen 53° = 0,8 e cos 53° = 0,6)
a) 480 J
b) 640 J
c) 960 J
d) 1280 J
e) 1600 J
Resposta:
[C]
Aplicação de fórmula: W  F.d.cos   80x20x0,6  960J
Página 6 de 13
Professora FLORENCE
10. (Ufsm 2011) Não se percebe a existência do ar num dia sem vento; contudo, isso não
significa que ele não existe. Um corpo com massa de 2kg é abandonado de uma altura de
10m, caindo verticalmente num referencial fixo no solo. Por efeito da resistência do ar, 4J da
energia mecânica do sistema corpo-Terra se transformam em energia interna do ar e do corpo.
Considerando o módulo de aceleração da gravidade como g= 10m/s2, o corpo atinge o solo
com velocidade de módulo,
em m/s, de
a) 12.
b) 14.
c) 15.
d) 16.
e) 18.
Resposta:
[B]
Como foram dissipados 4 J de energia mecânica do corpo, o trabalho das forças não
conservativas é igual a – 4 J. Assim, aplicando o teorema da energia cinética, vem:
WRv  Ecin

2 10 10   4 
WPv  WFv
não  conserv
2 v2
2

final
 Ecin
 Einicial
cin
v 2  196

m gh4
m v2
2


v  14 m / s.
11. (G1 - ifce 2011) Um bloco de massa igual a 10 kg é empurrado, a partir do repouso, por
uma força resultante constante de 10 N, que atua na mesma direção do movimento. O trabalho
realizado pela força e a velocidade desse bloco, após percorrer 12,5 metros, valem,
respectivamente,
a) 100 J e 125 m/s.
b) 125 J e 100 m/s.
c) 125 J e 5 m/s.
d) 100 J e 5 m/s.
e) 5 J e 125 m/s.
Resposta:
[C]
Dados: m = 10 kg; R = 10 N; S = 12,5 m.
Calculando o trabalho da resultante:
WRv  F S  10  12,5

WRv  125 J.
A velocidade pode ser calculada pelo teorema da energia cinética:
WRv  ECin 
m v 2 m v 02

2
2

125 
10 v 2
0
2

v  5 m / s.
12. (Fuvest 2011) Um esqueitista treina em uma pista cujo perfil está representado na figura
abaixo. O trecho horizontal AB está a uma altura h = 2,4 m em relação ao trecho, também
horizontal, CD. O esqueitista percorre a pista no sentido de A para D. No trecho AB, ele está
com velocidade constante, de módulo v = 4 m/s; em seguida, desce a rampa BC, percorre o
trecho CD, o mais baixo da pista, e sobe a outra rampa até atingir uma altura máxima H, em
Página 7 de 13
Professora FLORENCE
relação a CD. A velocidade do esqueitista no trecho CD e a altura máxima H são,
respectivamente, iguais a
NOTE E ADOTE
2
g = 10 m/s
Desconsiderar:
- Efeitos dissipativos.
- Movimentos do esqueitista em relação ao esqueite.
a) 5 m/s e 2,4 m.
b) 7 m/s e 2,4 m.
c) 7 m/s e 3,2 m.
d) 8 m/s e 2,4 m.
e) 8 m/s e 3,2 m.
Resposta:
[E]
Dados: h = 2,4 m; vAB = 4 m/s.
Usando duas vezes a conservação da energia mecânica:
2
m v CD
v2
m v 2AB
42
AB
CD


EMec
 EMec
 mgh 
 10(2, 4)  CD
2
2
2
2
2
2
m v CD
8
CD
E
EMec
 EMec

 mgH 
 10 H  H = 3,2 m.
2
2
2
 v CD
 64  vCD = 8 ms.
13. (Enem 2011) Uma das modalidades presentes nas olimpíadas é o salto com vara. As
etapas de um dos saltos de um atleta estão representadas na figura:
Página 8 de 13
Professora FLORENCE
Desprezando-se as forças dissipativas (resistência do ar e atrito), para que o salto atinja a
maior altura possível, ou seja, o máximo de energia seja conservada, é necessário que
a) a energia cinética, representada na etapa I, seja totalmente convertida em energia potencial
elástica representada na etapa IV.
b) a energia cinética, representada na etapa II, seja totalmente convertida em energia potencial
gravitacional, representada na etapa IV.
c) a energia cinética, representada na etapa I, seja totalmente convertida em energia potencial
gravitacional, representada na etapa III.
d) a energia potencial gravitacional, representada na etapa II, seja totalmente convertida em
energia potencial elástica, representada na etapa IV.
e) a energia potencial gravitacional, representada na etapa I, seja totalmente convertida em
energia potencial elástica, representada na etapa III.
Resposta:
[C]
Pela conservação da energia mecânica, toda energia cinética que o atleta adquire na etapa I, é
transformada em energia potencial na etapa III, quando ele praticamente para no ar.
OBS: Cabe ressaltar que o sistema é não conservativo (incrementativo), pois no esforço
para saltar, o atleta consome energia química do seu organismo, transformando parte em
energia mecânica, portanto, aumentando a energia mecânica do sistema.
14. (G1 - ifsp 2011) Um atleta de salto com vara, durante sua corrida para transpor o obstáculo
a sua frente, transforma a sua energia _____________ em energia ____________ devido ao
ganho de altura e consequentemente ao/à _____________ de sua velocidade.
As lacunas do texto acima são, correta e respectivamente, preenchidas por:
a) potencial – cinética – aumento.
b) térmica – potencial – diminuição.
c) cinética – potencial – diminuição.
d) cinética – térmica – aumento.
e) térmica – cinética – aumento.
Resposta:
[C]
Página 9 de 13
Professora FLORENCE
No salto com vara, o atleta transforma energia cinética em energia potencial gravitacional.
Devido ao ganho de altura, ocorre diminuição de sua velocidade.
TEXTO PARA A PRÓXIMA QUESTÃO:
Dados:
Aceleração da gravidade: 10 m/s2
Densidade da água: 103 kg/m3
Velocidade da luz no vácuo: 3  108 m/s
sen
cos
30º
0,50
0,86
37º
0,60
0,80
45º
0,71
0,71
15. (Ufpe 2011) O gráfico seguinte mostra como a energia potencial de uma partícula varia
com a sua posição. O valor da energia mecânica da partícula, EM , também aparece no gráfico.
A partícula de massa 0,1 kg se move em linha reta. Todas as forcas que atuam na partícula
são conservativas. Obtenha a velocidade máxima da partícula, em m/s.
Resposta:
Dados: m = 0,1 kg; EM = 45 J.
Como o sistema é conservativo, a velocidade é máxima no ponto onde a energia cinética
máxima, ou seja, onde a energia potencial é mínima.
Analisando o gráfico, o mínimo valor da energia potencial é zero quando a energia cinética é
máxima, igual a 45 J.
Assim:
2
mvmáx
 Ecin
máx
2

2
0,1 vmáx
 45  vmáx 
2
45  2 
0,1
 900 
vmáx  30m / s.
16. (Fgv 2010) Contando que ao término da prova os vestibulandos da GV estivessem loucos
por um docinho, o vendedor de churros levou seu carrinho até o local de saída dos candidatos.
Para chegar lá, percorreu 800 m, metade sobre solo horizontal e a outra metade em uma
ladeira de inclinação constante, sempre aplicando sobre o carrinho uma força de intensidade
30 N, paralela ao plano da superfície sobre a qual se deslocava e na direção do movimento.
Levando em conta o esforço aplicado pelo vendedor sobre o carrinho, considerando todo o
traslado, pode-se dizer que,
Página 10 de 13
Professora FLORENCE
a) na primeira metade do trajeto, o trabalho exercido foi de 12 kJ, enquanto que, na segunda
metade, o trabalho foi maior.
b) na primeira metade do trajeto, o trabalho exercido foi de 52 kJ, enquanto que, na segunda
metade, o trabalho foi menor.
c) na primeira metade do trajeto, o trabalho exercido foi nulo, assumindo, na segunda metade,
o valor de 12 kJ.
d) tanto na primeira metade do trajeto como na segunda metade, o trabalho foi de mesma
intensidade, totalizando 24 kJ.
e) o trabalho total foi nulo, porque o carrinho parte de um estado de repouso e termina o
movimento na mesma condição.
Resposta:
[D]
Dados: F = 30 N; S = 800 m.
O trabalho (W) de uma força constante ( F ) é dado pela expressão:
WF  F S cos . Como a força é paralela ao deslocamento,  = 0°, cos  = 1. Então:
WF  30 (800) = 24.000 J = 24 kJ.
17. (Pucrj 2010) O Cristo Redentor, localizado no Corcovado, encontra-se a 710 m do nível no
mar e pesa 1.140 ton. Considerando-se g = 10 m/s2, é correto afirmar que o trabalho total
realizado para levar todo o material que compõe a estátua até o topo do Corcovado foi de, no
mínimo:
a) 114.000 kJ
b) 505.875 kJ
c) 1.010.750 kJ
d) 2.023.500 kJ
e) 8.094.000 kJ
Resposta:
[E]
Dados: m = 1.140 ton = 1,14  106 kg; h = 710 m; g = 10 m/s2.
WF = m g h = (1,14  106) (10) (710) = 8,094  109 J = 8.094.000  103 J 
WF = 8.094.000 kJ.
18. (G1 - cftsc 2010) A ilustração abaixo representa um bloco apoiado sobre uma superfície
horizontal com atrito, puxado por uma força F com velocidade constante.
Com base na ilustração acima e na situação descrita no enunciado, é correto afirmar que:
a) o trabalho realizado pela força F é nulo.
b) o trabalho total realizado sobre o bloco é nulo.
Página 11 de 13
Professora FLORENCE
c) o trabalho realizado pela força de atrito f é nulo.
d) o trabalho realizado pela força de atrito f é positivo.
e) o trabalho realizado pela força F é igual à variação da energia cinética do bloco.
Resposta:
[B]
O teorema da energia cinética afirma que o trabalho da resultante é igual à variação da energia
cinética. Como a velocidade é constante, a variação da energia cinética é nula, sendo, então,
nulo, o trabalho da resultante (trabalho total) realizado sobre o bloco.
19. (Ufpb 2010) Um foguete de 1 tonelada de massa viaja com uma velocidade de 360 km/h
em uma região do espaço onde as forças da gravidade são desprezíveis. Em um determinado
momento, seus motores são acionados e, após a queima de 200 kg de combustível, sua
velocidade passa a ser de 720 km/h.
Com base no que foi exposto, é correto afirmar que o trabalho realizado sobre o foguete pelo
motor, durante a queima do combustível, corresponde a:
a) 4,7 x 107 J
b) 1,1 x 107 J
c) 1,5 x 107 J
d) 1,4 x 107 J
e) 1,9 x 107 J
Resposta:
[B]
Dados: m1 = 1.000 kg; v1 = 360 km/h = 100 m/s; m2 = 800 kg; v 2 = 720 km/h = 200 m/s.
Aplicando o teorema da energia cinética:
1.000 100 
m2 v 22 m1v12 800  200 



 1,6  107  0,5  107 
2
2
2
2
2
Wres  Ecin 
2
Wres  1,1 107 J.
20. (Ufla 2010) Um esquilo “voador” consegue planar do alto de uma árvore, a uma altura de
10 m até o chão, com velocidade constante de 5 m/s. Considerando a aceleração da gravidade
g = 10 m/s2 e a massa do esquilo 2 kg, é CORRETO afirmar que o trabalho da força de
sustentação que atua sobre o esquilo ao longo desse deslocamento é de
a) 50 J.
b) – 200 J.
c) – 20 J.
d) – 25 J.
Resposta:
[B]
2
Dados: v = 10 m/s; g = 10 m/s ; h = 10 m; m = 2 kg.
Página 12 de 13
Professora FLORENCE
 
 
Enquanto voa, no esquilo agem duas forças: o peso P e a força de sustentação Far do ar.
 
Como a velocidade é constante, o trabalho da resultante R é nulo. Mas o trabalho da
resultante é igual ao somatório dos trabalhos das forças atuantes. Assim:
WR  0  WP  WFar  0  m g h =  WFar
 WFar  – 2 (10) (10) 
WFar  – 200 J.
Página 13 de 13