Exercícios resolvidos

73
Curso Básico de Mecânica dos Fluidos
1.12.3 Exercícios resolvidos
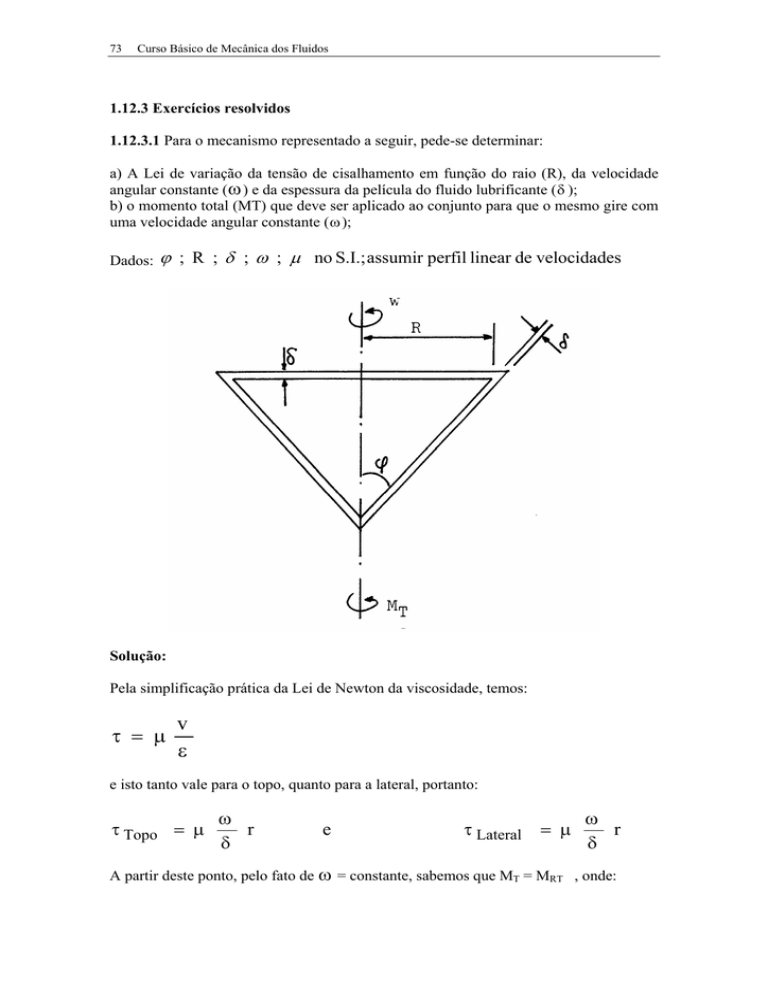
1.12.3.1 Para o mecanismo representado a seguir, pede-se determinar:
a) A Lei de variação da tensão de cisalhamento em função do raio (R), da velocidade
angular constante (ω ) e da espessura da película do fluido lubrificante (δ );
b) o momento total (MT) que deve ser aplicado ao conjunto para que o mesmo gire com
uma velocidade angular constante (ω );
Dados:
ϕ ; R ; δ ; ω ; µ no S.I.; assumir perfil linear de velocidades
Solução:
Pela simplificação prática da Lei de Newton da viscosidade, temos:
τ = µ
v
ε
e isto tanto vale para o topo, quanto para a lateral, portanto:
τ Topo = µ
ω
r
δ
e
τ Lateral = µ
ω
r
δ
A partir deste ponto, pelo fato de ω = constante, sabemos que MT = MRT , onde:
74
Curso Básico de Mecânica dos Fluidos
MRT = MRT Topo + MR lateral
Devemos notar que neste exercício, tanto a tensão de cisalhamento, como a área de
contato são função do raio, o que implica dizer que o momento resistente também o
será, o que nos obriga a trabalhar de forma diferencial, portanto:
Topo:
dMRtopo =dFµTopo ×r =τTopo ×dATopo ×r
ω
r 2πr dr × r
δ
R 2πωµ
3
=
dM
Rtopo
∫
∫0 δ r dr
R
2πωµ 3
2πωµ R4
MRtopo =
r
dr
=
δ ∫0
δ 4
dMRtopo = µ
πωµR4
∴MRtopo =
2δ
Lateral:
d M RLat = dFµL × r = τL × d A Lat . × r
d M RLat = µ
ω
r dA L × r
δ
75
Curso Básico de Mecânica dos Fluidos
dAL = ?
dAL = 2 π r dx , onde:
x=
R
R
sen ϕ
∴dx =
dr
sen α
e dA L = 2πr
ϕ
ω
d
r 2π r R × r
δ
sen ϕ
2π ω µ 3
=
r dr
δ sen ϕ
d M RL = µ
d M RL
M RL
2π ω µ
=
δ sen ϕ
R
∫r
3
dr
0
π ω µ R4 π ω µ R4
∴ MT =
+
2δ
2 δ senϕ
π ω µ R4
1
MT =
⋅(1+
)
2δ
sen ϕ
∴ M RL
π ω µ R4
=
2 δ senϕ
dr
sen ϕ
76
Curso Básico de Mecânica dos Fluidos
1.12.3.2 Na figura, vê-se uma placa plana de área 1 m² que desliza sobre um plano
inclinado de 30° com a horizontal. A placa tem peso de 200 N e entre a placa e
o plano existe uma película de óleo lubrificante de viscosidade dinâmica igual
à 10 - 2 N × s / m 2 e espessura de 1 mm. A parte superior da placa está presa
a uma corda que passa por roldanas, sem atrito e na outra extremidade está
preso um pistão cilíndrico de peso 80 N. O pistão, de diâmetro 10 cm, corre
dentro de um cilindro de diâmetro interno igual a 10,2 cm e a folga anular
entre os dois é preenchida com um óleo lubrificante de viscosidade dinâmica
igual a 0,3 N×s/m². Determine a velocidade de descida da placa, supondo
diagrama linear de velocidades nos dois lubrificantes.
Solução:
Placa =>
1) considerando sem o fluido lubrificante
Resultante =>
Rplaca = G t - T
Rplaca = 100 - T
2) considerando a presença do fluido lubrificante
Fµ placa = Rplaca
Fµ placa = 100 - T = τ p × Ap
µp ×
Pistão =>
vp
εp
× A p = 100 − T
→
10 v p = 100 - T (I)
1) considerando sem a presença do fluido lubrificante
Resultante =>
Rc = T - Gc
Rc = T - 80
2) considerando a presença do fluido lubrificante
77
Curso Básico de Mecânica dos Fluidos
Fµ c = Rc
Fµ c = T - 80 = τ c × Ac
v
µ c × c × A c = T - 80
εc
→
30 v c = T - 80 (II)
Pela condição do exercício, temos:
vp = vc = v = constante , portanto:
10 v = 100 - 30 v - 80
40 v = 20
∴ v = 0,5 m/s
1.12.3.3 Calcule o momento resistente originado pelo óleo lubrificante em contato com
o eixo vertical esquematizado abaixo. Sabe-se que o eixo apresenta uma rotação
constante de 3000 rpm.
78
Curso Básico de Mecânica dos Fluidos
Solução:
n => origina no eixo uma velocidade angular ω
ω = 2 π n → ( rps ) =
2πn
→ ( rpm ) = 100 π rad / s
60
ω => origina no eixo uma velocidade escalar v
v = ω × Re = 10 π m/s
O fluido com viscosidade µ, origina no eixo uma força de resistência viscosa Fµ
Fµ = τ × Ac = µ ×
ε = Rm − Re =
Fµ = 40 π
2
v0
ε
× π × De × L
( Dm − De )
2
(N)
Fµ => origina no eixo um momento contrário ao movimento, que é denominado de
momento resistente (MR ):
MR = Fµ × Re = 39,48 N×m
1.12.3.4 Determine a expressão para o cálculo do peso G da configuração
esquematizada abaixo.
Dados:
n => em rps
Dm
;
Dc
;
De
;
L
e
µ => no S.I.
79
Curso Básico de Mecânica dos Fluidos
Solução:
Para a solução deste exercício, representamos a situação esquematizada pela figura em
duas etapas, respectivamente as figuras A e B.
A reação T origina para o eixo um momento, que é responsável pela ''criação'' da
rotação (n) do sistema. Este momento é denominado de momento motor (Mm )
Mm =T
De
D
=G e ∴
2
2
G=
2× Mm
(I)
De
Figura B
Considerando o ponto P1 na interseção do eixo qualquer com o cilindro, temos:
n → origina
ω para o cilindro → ω = 2 π n
ω → origina v para o cilindro → v = π n Dc
µ → origina Fµ para o cilindro → Fµ = τ × Ac
80
Curso Básico de Mecânica dos Fluidos
2 × π 2 × n × Dc2 × L
Fµ = µ × × π D c L → Fµ =
ε
(D m − D c )
D
Fµ → origina MR para o cilindro → M R = Fµ × c
2
2
3
µ π n Dc L
MR =
(II)
Dm − Dc
v
Como n = constante, das equação (I) e (II) temos: G =
2 µ π 2 n D 3c L
De ⋅ ( D m − Dc )
1.12.3.5 Um corpo trapezoidal desce sobre um plano inclinado de 45º com o plano
horizontal, como mostra a figura. Sabendo-se que tanto as polias como os fios são ideais
e que utilizou-se um fluido lubrificante de viscosidade cinemática igual a 400 cSt, pedese determinar o peso do corpo trapezoidal (G3) no SI e no CGS.
Dados:
γ H O = 10 4 N m 3 ; γ r = 0,75 ; g = 9,81m / s 2 ; G1 = 20 N
2
D1 = 0,201m ; DC1 = 0,203m ; L =
2
π
m ; v = 0,5 m/s
Solução:
υ = 400 cSt = 400 × 10 - 2 St = 400 × 10 - 6 m²/s
υ=
γr γH O
µ
γ
→ µ =υ ⋅ ρ =υ ⋅ → µ =υ
g
g
ρ
2
81
Curso Básico de Mecânica dos Fluidos
G3 sen 45º = T + 0,30581
G3 sen 45º = T + 95,57
0, 5
(1 ×1,5 + 0,75 × 0,5)
3 × 10 - 3
(I)
T1 = 78,79 N
Substituindo em (III), temos:
G3 sen 45º = T1 + 120,04
G3 sen 45º = 78,79 + 120,04
G3 sen 45º = 281,19 N => SI
1 N=105 dina, portanto: 281,19 N=281,19 × 105 dina => CGS
82
Curso Básico de Mecânica dos Fluidos
Na foto: eu, a Lia, o Vinícius e o Marcus Vinícius
Existem aqueles que perdem
Existem aqueles que ganham
Existem aqueles que esperam
Simplesmente porque amam
Raimundo Ferreira Ignácio